INCOMING TRANSMISSION

LATEST UPDATES
ALL WIP FAV

漫谈重参数：从正态分布到Gumbel Softmax

Deep Learning
2025-01-11
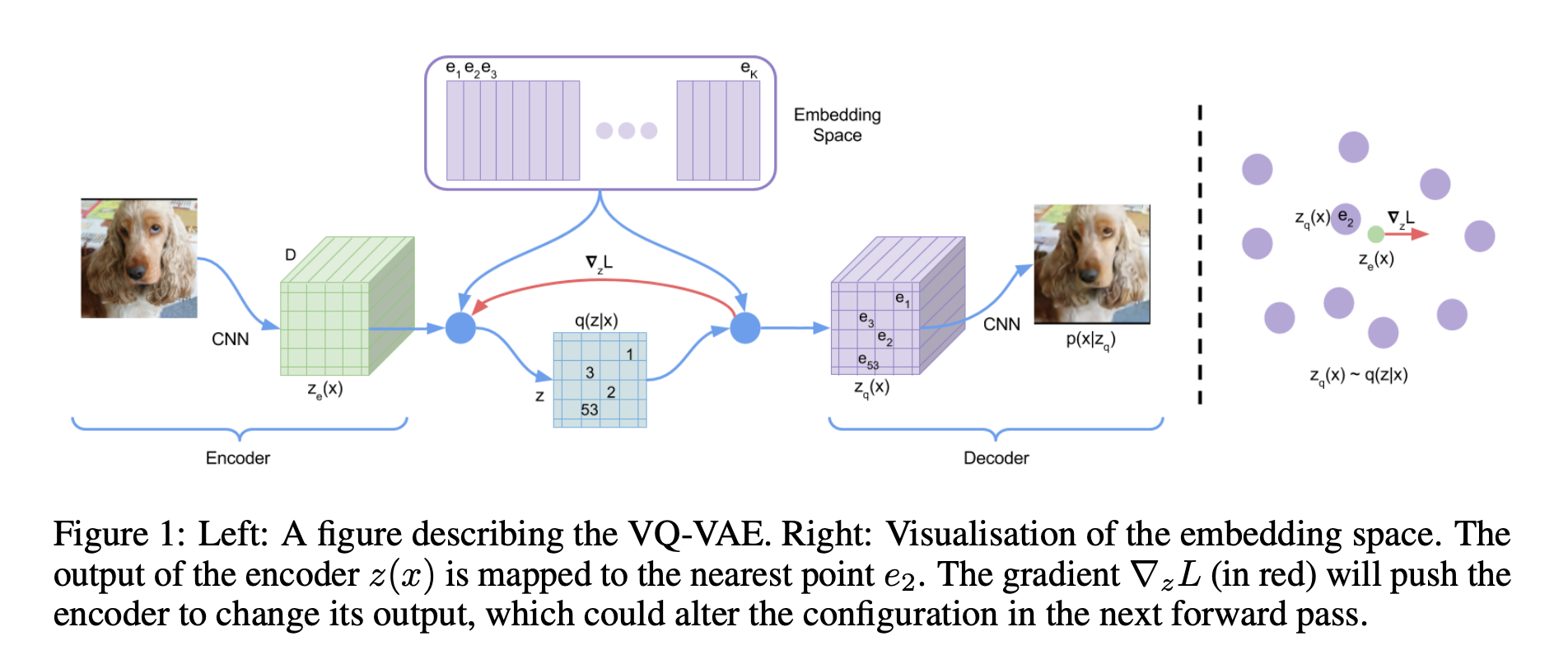
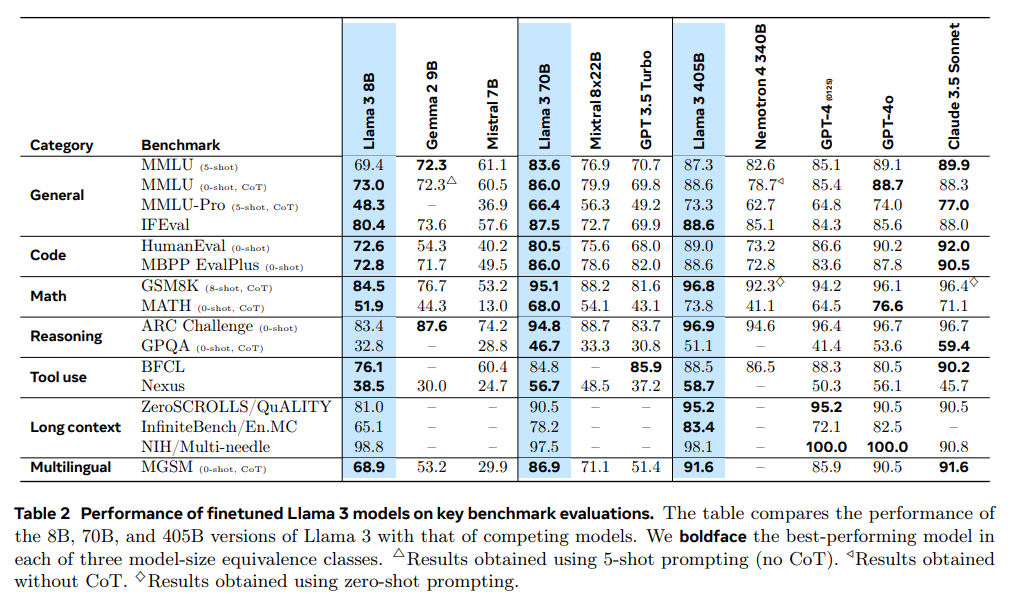
文章从连续情形出发开始介绍重参数，主要的例子是正态分布的重参数；然后引入离散分布的重参数，这就涉及到了Gumbel Softmax，包括Gumbel Softmax的一些证明和讨论；最后再讲讲重参数背后的一些故事，这主要跟梯度估计有关。 基本概念 重参数（Reparameterization）实际上是处理如下期望形式的目标函数的一种技巧： [公式] 这样的目标在VAE中会出现，在文本GAN也会出现，在强化学习中也会出现（ f(z) 对应于奖励函数），所以深究下去，我们会经常碰到这样的目标函数。取决于 z 的连续性，它对应不同的形式： [公式] 当然，离散情况下我们更喜欢将记号 z 换成 y 或者 c 。 为了最小化 [Math] ，我们就需要把 [Math] 明确地写出来，这意味着我们要实现...
#DL基础 #VAE
READ

函数光滑化：不可导函数的可导逼近

Deep Learning
2025-01-11
一般来说，神经网络处理的东西都是连续的浮点数，标准的输出也是连续型的数字。但实际问题中，我们很多时候都需要一个离散的结果，比如分类问题中我们希望输出正确的类别，“类别”是离散的，“类别的概率”才是连续的；又比如我们很多任务的评测指标实际上都是离散的，比如分类问题的正确率和F1、机器翻译中的BLEU，等等。 还是以分类问题为例，常见的评测指标是正确率，而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联，但它们不是绝对的单调相关关系。换句话说，交叉熵下降了，正确率不一定上升。显然，如果能用正确率的相反数做损失函数，那是最理想的，但正确率是不可导的（涉及到 [Math] 等操作），所以没法直接用。 这时候一般有两种解决方案；一是动用强化学习，将正确率设为奖励函数，这是“用牛刀杀...
#DL基础
READ

VQ-VAE

Generative Model
2025-01-10
简介 作为一个自编码器，VQVAE的一个明显特征是它编码出的编码向量是离散的，换句话说，它最后得到的编码向量的每个元素都是一个整数，这也就是“Quantised”的含义，我们可以称之为“量子化”（跟量子力学的“量子”一样，都包含离散化的意思）。 明明整个模型都是连续的、可导的，但最终得到的编码向量却是离散的，并且重构效果看起来还很清晰（如文章开头的图），这至少意味着VQVAE会包含一些有意思、有价值的技巧，值得我们学习一番。 首先，VQVAE其实就是一个AE（自编码器）而不是VAE（变分自编码器），我不知道作者出于什么目的非得用概率的语言来沾VAE的边，这明显加大了读懂这篇论文的难度。其次，VQVAE的核心步骤之一是StraightThrough Estimator，这是将引变量离散化后的优...
#VAE #Generating Model
READ

Flow Matching

Generative Model
2025-01-09
💡 Flowbased Models Normalizing Flow Normalizing Flow 是一种基于变换对概率分布进行建模的模型，其通过一系列离散且可逆的变换实现任意分布与先验分布（例如标准高斯分布）之间的相互转换。在 Normalizing Flow 训练完成后，就可以直接从高斯分布中进行采样，并通过逆变换得到原始分布中的样本，实现生成的过程。（有关 Normalizing Flow 的详细理论） 从这个角度看，Normalizing Flow 和 Diffusion Model 是有一些相通的，其做法的对比如下表所示。从表中可以看到，两者大致的过程是非常类似的，尽管依然有些地方不一样，但这两者应该可以通过一定的方法得到一个比较统一的表示。 Continuous Norma...
#Generating Model #flow #diffusion
READ

Diffusion Models扩散模型

Generative Model
2025-01-08
扩散模型的物理背景 点云扩散过程 初中化学/物理就学过扩散运动，布朗运动就是一种典型的扩散过程。如果你忘了，可以复习复习： 布朗运动是指悬浮在液体或气体中的微粒所做的永不停息的无规则运动。其因由英国植物学家布朗所发现而得名。作布朗运动的微粒的直径一般为 105103 厘米，这些小的微粒处于液体或气体中时，由于液体分子的热运动，微粒受到来自各个方向液体分子的碰撞，当受到不平衡的冲撞时而运动，由于这种不平衡的冲撞，微粒的运动不断地改变方向而使微粒出现不规则的运动。布朗运动的剧烈程度随着流体的温度升高而增加。 刚才说的物理背景，重点就是：这是一种从有序到无序的过程。在深度学习中，什么是最典型的无序？没错，就是噪声。 除此之外，这种有序和无序之间的转换，在生成模型中大有用处。理论上任何生成模型都能应...
#diffusion #Generating Model
READ

SDE和扩散模型

Generative Model
2025-01-08
💡 随机微分 在DDPM中，扩散过程被划分为了固定的T步，还是用DDPM中的类比来说，就是“拆楼”和“建楼”都被事先划分为了T步，这个划分有着相当大的人为性。事实上，真实的“拆”、“建”过程应该是没有刻意划分的步骤的，我们可以将它们理解为一个在时间上连续的变换过程，可以用随机微分方程（Stochastic Differential Equation，SDE）来描述。 为此，我们用下述SDE描述前向过程（“拆楼”）： [公式] 相信很多读者都对SDE很陌生，笔者也只是在硕士阶段刚好接触过一段时间，略懂皮毛。不过不懂不要紧，我们只需要将它看成是下述离散形式在 [Math] 时的极限： [公式] 再直白一点，如果假设拆楼需要1天，那么拆楼就是 [Math] 从 t=0 到 t=1 的变化过程，每一...
#SDE #diffusion #Generating Model
READ

DDPM

Generative Model
2025-01-08
💡 扩散模型：通过加噪的方式去学习原始数据的分布， 从学到的分布中去生成样本 “拆楼建楼”角度理解 很多文章在介绍DDPM时，上来就引入转移分布，接着就是变分推断，一堆数学记号下来，先吓跑了一群人（当然，从这种介绍我们可以再次看出，DDPM实际上是VAE而不是扩散模型），再加之人们对传统扩散模型的固有印象，所以就形成了“需要很高深的数学知识”的错觉。事实上，DDPM也可以有一种很“大白话”的理解，它并不比有着“造假鉴别”通俗类比的GAN更难。 首先，我们想要做一个像GAN那样的生成模型，它实际上是将一个随机噪声 [Math] 变换成一个数据样本 [Math] 的过程： [公式] 我们可以将这个过程想象为“建设”，其中随机噪声 [Math] 是砖瓦水泥等原材料，样本数据 [Math] 是高楼大...
#diffusion #Generating Model
READ

Consistency Models

Generative Model
2025-01-05
Diffusion Models from SDE 连续扩散模型 (Continuous Diffusion Models) 将传统的离散时间扩散过程扩展到连续时间域,可以被视为一个随机过程，使用随机微分方程(SDE)来描述。其前向过程可以写成如下形式： [公式] 其中， f(x,t) 可以看成偏移系数， g(t) 可以看成是扩散系数， dw 是标准布朗运动。这个SDE 描述了数据在连续时间域内如何被噪声逐渐破坏。 这个随机过程的逆向过程存在（更准确的描述：下面的逆向时间SDE具有与正向过程SDE相同的联合分布）为 [公式] 前面我们得到了扩散过程的逆向过程可以用一个SDE描述(逆向随机过程),事实上，存在一个确定性过程 (用ODE描述)也是它的逆向过程 (更准确的描述：这个ODE过程的在任...
#ODE #SDE #Generating Model #diffusion
READ

Llama系列

Large Model
2025-01-04
LLaMA 一直致力于LLM模型研究的国外TOP 3大厂除了OpenAI、Google，便是Meta(原来的Facebook) Meta曾第一个发布了基于LLM的聊天机器人——BlenderBot 3，但输出不够安全，很快下线；再后来，Meta发布一个专门为科学研究设计的模型Galactica，但用户期望过高，发布三天后又下线 23年2.24日，Meta通过论文《LLaMA: Open and Efficient Foundation Language Models》发布了自家的大型语言模型LLaMA，有多个参数规模的版本(7B 13B 33B 65B)，并于次月3.8日被迫开源 LLaMA只使用公开的数据(总计1.4T即1,400GB的token，其中CommonCrawl的数据占比67%...
#LLM
READ

Llama 3.1

Large Model
2025-01-04
🔖 https://ai.meta.com/research/publications/thellama3herdofmodels/ 简介 本文归纳llm的训练分为两个主要阶段： 预训练阶段 pretraining，模型通过使用简单的任务如预测下一个词或caption进行大规模训练 后训练阶段 posttraining，模型经过调整以遵循指令、与人类偏好保持一致，并提高特定能力, 例如编码和推理。 Llama 3.1 发布，在 15.6T 多语言 tokens 上训练，支持多语言，编程，推理和工具使用。新模型支持 128K tokens 长度的上下文。最大的旗舰模型参数量为 405B，效果达到了闭源模型的 SOTA。 模型结构 Llama 3.1 的模型和 Llama 3 是一样的，只是做了...
#LLM
READ

随机游走问题

Math
2025-01-03
问题表示 有很多概率问题，尤其是独立重复实验问题，如果用生成函数的方法来做，会显得特别方便。本文要讲的“随机游走”问题便是其中一例，它又被形象地叫做“醉汉问题”，其本质上是一个二项分布，但是由于取了极限，出现了很多新的性质和应用。我们先考虑如下问题： 考虑实数轴上的一个粒子，在 t=0 时刻它位于原点，每过一秒，它要不向前移动一格（+1），要不就向后移动一格（1），问 n 秒后它所处位置的概率分布。 不难发现，这个问题跟二项分布是雷同的。如果把这个粒子形象比喻成一个“喝醉酒的人”，那么上面的走法就类似于一个完全不省人事的醉汉走路问题了。（当然，醉汉是在三维空间走路的，这里简单起见，只描述了一维的。）这是一个独立重复实验，每秒的行走可用函数描述为 [Math] ，于是 n 秒后的运动分布情况可...
#math
READ

Gaze采集标定方案

3D Model
2025-01-02
整体流程： [代码] 0. 数据预处理 这个步骤主要是crop四路数据，及生成后续步骤所需要的yaml文件。 1. 四路相机与双路相机标定 内参标定 [代码] 这里主要的函数就是： pts = cv2.findChessboardCorners(img, (board_width, board_height))[1] cv2.cornerSubPix(gray, pts, (12, 12), (1, 1), (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_COUNT, 30, 0.1)) det, intr, dist, _, _ = cv2.calibrateCamera(obj_pts, img_pts, self.imgSize, None, No...
#3D
READ
1 ... 6 7 8 9 10 ... 24