简介

作为一个自编码器，VQ-VAE的一个明显特征是它编码出的编码向量是离散的，换句话说，它最后得到的编码向量的每个元素都是一个整数，这也就是“Quantised”的含义，我们可以称之为“量子化”（跟量子力学的“量子”一样，都包含离散化的意思）。

明明整个模型都是连续的、可导的，但最终得到的编码向量却是离散的，并且重构效果看起来还很清晰（如文章开头的图），这至少意味着VQ-VAE会包含一些有意思、有价值的技巧，值得我们学习一番。

首先，VQ-VAE其实就是一个AE（自编码器）而不是VAE（变分自编码器），我不知道作者出于什么目的非得用概率的语言来沾VAE的边，这明显加大了读懂这篇论文的难度。其次，VQ-VAE的核心步骤之一是Straight-Through Estimator，这是将引变量离散化后的优化技巧，在原论文中没有稍微详细的讲解，以至于必须看源码才能更好地知道它说啥。最后，论文的核心思想也没有很好地交代清楚，给人的感觉是纯粹在介绍模型本身而没有介绍模型思想。

PixelCNN

要追溯VQ-VAE的思想，就不得不谈到自回归模型。可以说，VQ-VAE做生成模型的思路，源于PixelRNN、PixelCNN之类的自回归模型，这类模型留意到我们要生成的图像，实际上是离散的而不是连续的。以cifar10的图像为例，它是$32×32$大小的3通道图像，换言之它是一个$32×32×3$的矩阵，矩阵的每个元素是0～255的任意一个整数，这样一来，我们可以将它看成是一个长度为$32×32×3=3072$的句子，而词表的大小是256，从而用语言模型的方法，来逐像素地、递归地生成一张图片（传入前面的所有像素，来预测下一个像素），这就是所谓的自回归方法：

\[ \begin{equation}p(x)=p(x_1)p(x_2|x_1)\dots p(x_{3n^2}|x_1,x_2,\dots,x_{3n^2-1})\end{equation} \]

其中$p(x_1),p(x_2|x_1),\dots,p(x_{3n^2}|x_1,x_2,\dots,x_{3n^2-1})$每一个都是256分类问题，只不过所依赖的条件有所不同。

PixelRNN、PixelCNN网上都有一定的资料介绍了，这里不再赘述，我感觉其实也可以蹭着Bert的热潮，去搞个PixelAtt（Attention）来做它。自回归模型的研究主要集中在两方面：一方面是如何设计这个递归顺序，使得模型可以更好地生成采样，因为图像的序列不是简单的一维序列，它至少是二维的，更多情况是三维的，这种情况下你是“从左往右再从上到下”、“从上到下再从左往右”、“先中间再四周”或者是其他顺序，都很大程度上影响着生成效果；另一方面是研究如何加速采样过程。

自回归的方法很稳妥，也能有效地做概率估计，但它有一个最致命的缺点：慢。因为它是逐像素地生成的，所以要每个像素地进行随机采样，上面举例的cifar10已经算是小图像的，目前做图像生成好歹也要做到$128×128×3$的才有说服力了吧，这总像素接近5万个（想想看要生成一个长度为5万的句子），真要逐像素生成会非常耗时。而且这么长的序列，不管是RNN还是CNN模型都无法很好地捕捉这么长的依赖。

原始的自回归还有一个问题，就是割裂了类别之间的联系。虽然说因为每个像素是离散的，所以看成256分类问题也无妨，但事实上连续像素之间的差别是很小的，纯粹的分类问题捕捉到这种联系。更数学化地说，就是我们的目标函数交叉熵是$−log⁡p_t$，假如目标像素是100，如果我预测成99，因为类别不同了，那么$p_t$就接近于0，$−log⁡p_t$就很大，从而带来一个很大的损失。但从视觉上来看，像素值是100还是99差别不大，不应该有这么大的损失。

VQ-VAE

针对自回归模型的固有毛病，VQ-VAE提出的解决方案是：先降维，然后再对编码向量用PixelCNN建模.

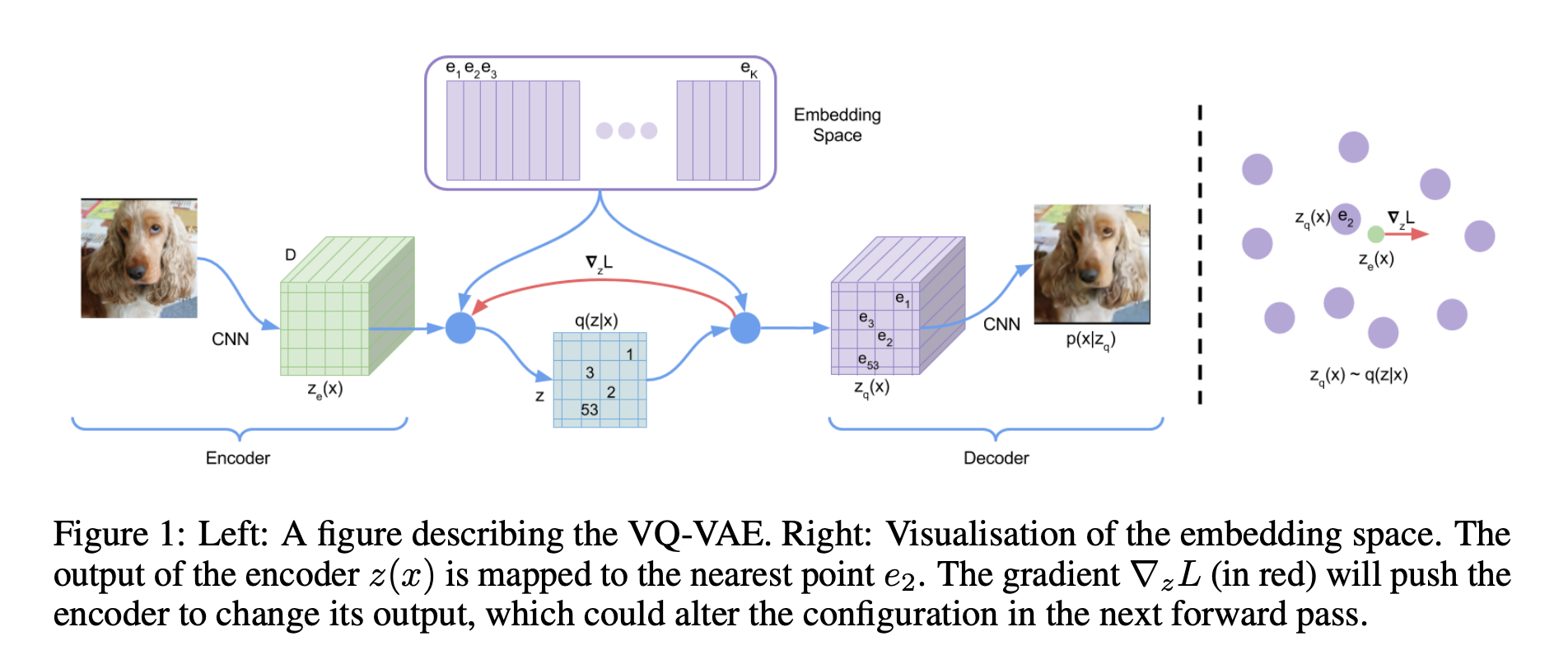
整个VQ-VAE的流程如上图，用文字描述就是：

Codebook是一个 $K\times D$ 的table, 对应上方紫色的 $e_1,e_2,...,e_K$ .
将一张图片经过Encoder后, 可以得到一个 $H^{'}\times W^{'}\times D$ 的feature map, 即绿色的 $z_e(x)$ .
将这 $H^{'}\times W^{'}$ 个 $D$ 维向量分别去codebook里找到最近的 $e_i$ , 用其index表示, 就得到了青色的 $q(z|x)$ .
把绿色的 $z_e(x)$ 用codebook里最近的 $e_i$ 替换后可以得到紫色的 $z_q(x)$ , 这是decoder的输入, 然后reconstruct得到图片.
多提一句, $q(z|x)$ 里每个数字都是一个离散的整数, 我们可以把这个数字写成one-hot的形式, 从而看成一个概率分布, 总共有 $K$ 维, 每一维代表对应codebook里 $e_i(i=1,2,...,K)$ 的概率. 从VAE的角度来看, 我们给这个$K$维分布一个均匀分布作为先验, 即 $p_i=\frac{1}{K}$ , 从而ELBO中 $KL(q_\phi(z|x)||p(z))$ 这一项就变成了一个常数:

\[ \begin{aligned} KL(q(z | x) ∥ p(z)) = & E_{z∼q(z|x) }log\frac{q(z|x)}{p(z)}\\ =&\sum_{k=1}^Kq(z=k|x)logq(z=k|x)-\sum_{k=1}^Kq(z=k|x)log\underbrace{p(z=k)}_{=\frac{1}{K}}\\ = &−H(q) + log K = log K \end{aligned} \]

降维离散化

看上去这个方案很自然，似乎没什么特别的，但事实上一点都不自然。

因为PixelCNN生成的离散序列，你想用PixelCNN建模编码向量，那就意味着编码向量也是离散的才行。而我们常见的降维手段，比如自编码器，生成的编码向量都是连续性变量，无法直接生成离散变量。同时，生成离散型变量往往还意味着存在梯度消失的问题。还有，降维、重构这个过程，如何保证重构之后出现的图像不失真？如果失真得太严重，甚至还比不上普通的VAE的话，那么VQ-VAE也没什么存在价值了。

幸运的是，VQ-VAE确实提供了有效的训练策略解决了这两个问题。

最邻近重构

在VQ-VAE中，一张 $n×n×3$的图片 $x$ 先被传入一个encoder中，得到连续的编码向量 $z$：

\[ \begin{equation}z = encoder(x)\end{equation} \]

这里的 $z$ 是一个大小为 $d$ 的向量。另外，VQ-VAE还维护一个Embedding层，我们也可以称为编码表，记为

\[ \begin{equation}E = [e_1, e_2, \dots, e_K]\end{equation} \]

这里每个 $e_i$ 都是一个大小为 $d$ 的向量。接着，VQ-VAE通过最邻近搜索，将 $z$ 映射为这 $K$ 个向量之一：

\[ \begin{equation}z\to e_k,\quad k = \mathop{\arg\min}_j \Vert z - e_j\Vert_2\end{equation} \]

我们可以将 $z$ 对应的编码表向量记为$z_q$，我们认为 $z_q$ 才是最后的编码结果。最后将$z_q$传入一个decoder，希望重构原图$\hat{x}=decoder(z_q)$。

整个流程是：

\[ \begin{equation}x\xrightarrow{encoder} z \xrightarrow{\text{最邻近}} z_q \xrightarrow{decoder}\hat{x}\end{equation} \]

这样一来，因为$z_q$是编码表 $E$ 中的向量之一，所以它实际上就等价于$1,2,…,K$这$K$个整数之一，因此这整个流程相当于将整张图片编码为了一个整数。

当然，上述过程是比较简化的，如果只编码为一个向量，重构时难免失真，而且泛化性难以得到保证。所以实际编码时直接用多层卷积将 $ x$ 编码为$m×m$个大小为$d$的向量：

\[ \begin{equation}z = \begin{pmatrix}z_{11} & z_{12} & \dots & z_{1m}\\ z_{21} & z_{22} & \dots & z_{2m}\\ \vdots & \vdots & \ddots & \vdots\\ z_{m1} & z_{m2} & \dots & z_{mm}\\ \end{pmatrix}\end{equation} \]

也就是说，$z$ 的总大小为$m×m×d$，它依然保留着位置结构，然后每个向量都用前述方法映射为编码表中的一个，就得到一个同样大小的$z_q$，然后再用它来重构。这样一来，$z_q$也等价于一个$m×m$的整数矩阵，这就实现了离散型编码。

自行设计梯度

我们知道，如果是普通的自编码器，直接用下述loss进行训练即可：

\[ \begin{equation}\Vert x - decoder(z)\Vert_2^2\end{equation} \]

但是，在VQ-VAE中，我们用来重构的是$z_q$而不是$z$，那么似乎应该用这个loss才对：

\[ \begin{equation}\Vert x - decoder(z_q)\Vert_2^2\end{equation} \]

但问题是$z_q$的构建过程包含了arg⁡min，这个操作是没梯度的，所以如果用第二个loss的话，我们没法更新encoder。

换言之，我们的目标其实是$‖x−decoder(z_q)‖^2_2$最小，但是却不好优化，而$‖x−decoder(z)‖^2_2$容易优化，但却不是我们的优化目标。那怎么办呢？当然，一个很粗暴的方法是两个都用：

\[ \begin{equation}\Vert x - decoder(z)\Vert_2^2 + \Vert x - decoder(z_q)\Vert_2^2\end{equation} \]

但这样并不好，因为最小化$‖x−decoder(z)‖_2^2$并不是我们的目标，会带来额外的约束。

VQ-VAE使用了一个很精巧也很直接的方法，称为Straight-Through Estimator，你也可以称之为“直通估计”，它最早源于Benjio的论文《Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation》，在VQ-VAE原论文中也是直接抛出这篇论文而没有做什么讲解。但事实上直接读这篇原始论文是一个很不友好的选择，还不如直接读源代码。

事实上Straight-Through的思想很简单，就是前向传播的时候可以用想要的变量（哪怕不可导），而反向传播的时候，用你自己为它所设计的梯度。根据这个思想，我们设计的目标函数是：

\[ \begin{equation}\Vert x - decoder(z + sg[z_q - z])\Vert_2^2\end{equation} \]

其中 $sg$ 是stop gradient的意思，就是不要它的梯度。这样一来，前向传播计算（求loss）的时候，就直接等价于$decoder(z+z_q−z)=decoder(z_q)$，然后反向传播（求梯度）的时候，由于$z_q−z$ 不提供梯度，所以它也等价于$decoder(z)$，这个就允许我们对 $encoder$ 进行优化了。

顺便说一下，基于这个思想，我们可以为很多函数自己自定义梯度，比如$x+sg[relu(x)−x]$ 就是将$relu(x)$的梯度定义为恒为1，但是在误差计算是又跟 $relu(x)$ 本身等价。当然，用同样的方法我们可以随便指定一个函数的梯度，至于有没有实用价值，则要具体任务具体分析了。

维护编码表

要注意，根据VQ-VAE的最邻近搜索的设计，我们应该期望 $z_q$ 和 $z$ 是很接近的（事实上编码表$E$的每个向量类似各个$z$的聚类中心出现），但事实上未必如此，即使 $‖x−decoder(z)‖^2_2$ 和$‖x−decoder(z_q)‖_2^2$都很小，也不意味着 $ z_q$ 和 $z$ 差别很小（即$f(z_1)=f(z_2)$不意味着$z_1=z_2$。

所以，为了让$z_q$和 $z$ 更接近，我们可以直接地将 $‖z−z_q‖^2_2$ 加入到loss中：

\[ \begin{equation}\Vert x - decoder(z + sg[z_q - z])\Vert_2^2 + \beta \Vert z - z_q\Vert_2^2\end{equation} \]

除此之外，还可以做得更仔细一些。由于编码表（$z_q$）相对是比较自由的，而 $z$ 要尽力保证重构效果，所以我们应当尽量“让$z_q$去靠近$z$”而不是“让$z$去靠近$z_q$”，而因为$‖z_q−z‖_2^2$的梯度等于对$z_q$的梯度加上对$z$的梯度，所以我们将它等价地分解为

\[ \begin{equation}\Vert sg[z] - z_q\Vert_2^2 + \Vert z - sg[z_q]\Vert_2^2\end{equation} \]

第一项相等于固定$z$，让$z_q$靠近z，第二项则反过来固定$z_q$，让$z$靠近$z_q$。注意这个“等价”是对于反向传播（求梯度）来说的，对于前向传播（求loss）它是原来的两倍。根据我们刚才的讨论，我们希望“让$z_q$去靠近$z$”多于“让$z$去靠近$z_q$”，所以可以调一下最终的loss比例：

\[ \begin{equation}\Vert x - decoder(z + sg[z_q - z])\Vert_2^2 + \beta \Vert sg[z] - z_q\Vert_2^2 + \gamma \Vert z - sg[z_q]\Vert_2^2\end{equation} \]

其中 $γ<β$，在原论文中使用的是$γ=0.25β$。

（注：还可以用滑动评论的方式更新编码表，详情请看原论文。）

拟合编码分布

VAE的目的是训练完成后, 丢掉encoder, 在prior上直接采样, 加上decoder就能生成. 如果我们现在独立地采$m\times m$ 个 $z$ , 然后查表得到维度为$m\times m\times d$的$z_q(x)$, 那么生成的图片在空间上的每块区域之间几乎就是独立的. 因此我们需要让各个 $z$ 之间有关系, 因此用PixelCNN, 对这些 $z$ 建立一个autoregressive model: $p(z_1,z_2,...,)=p(z_1)p(z_2|z_1)p(z_3|z_1,z_2)...$ , 这样就可以进行ancestral sampling, 得到一个互相之间有关联的$m\times m$的整数矩阵; $p(z_1,z_2,z_3,...)$ 这个联合概率即为我们想要的prior.

一般来说，现在的 $m×m$ 比原来的 $n×n×3$ 要小得多，比如我在用CelebA数据做实验的时候，原来 $128×128×3$ 的图可以编码为 $32×32$ 的编码而基本不失真，所以用自回归模型对编码矩阵进行建模，要比直接对原始图片进行建模要容易得多。

VQ-VAE-2

详细介绍了 VQ-VAE-1，那么 VQ-VAE-2 就很好解释了。如下图所示，左边是训练过程，分上下两层。上层潜在空间 32x32, 下层潜在空间大小 64 x 64。上层首先进行分层量子化，得到量子化后的字典向量

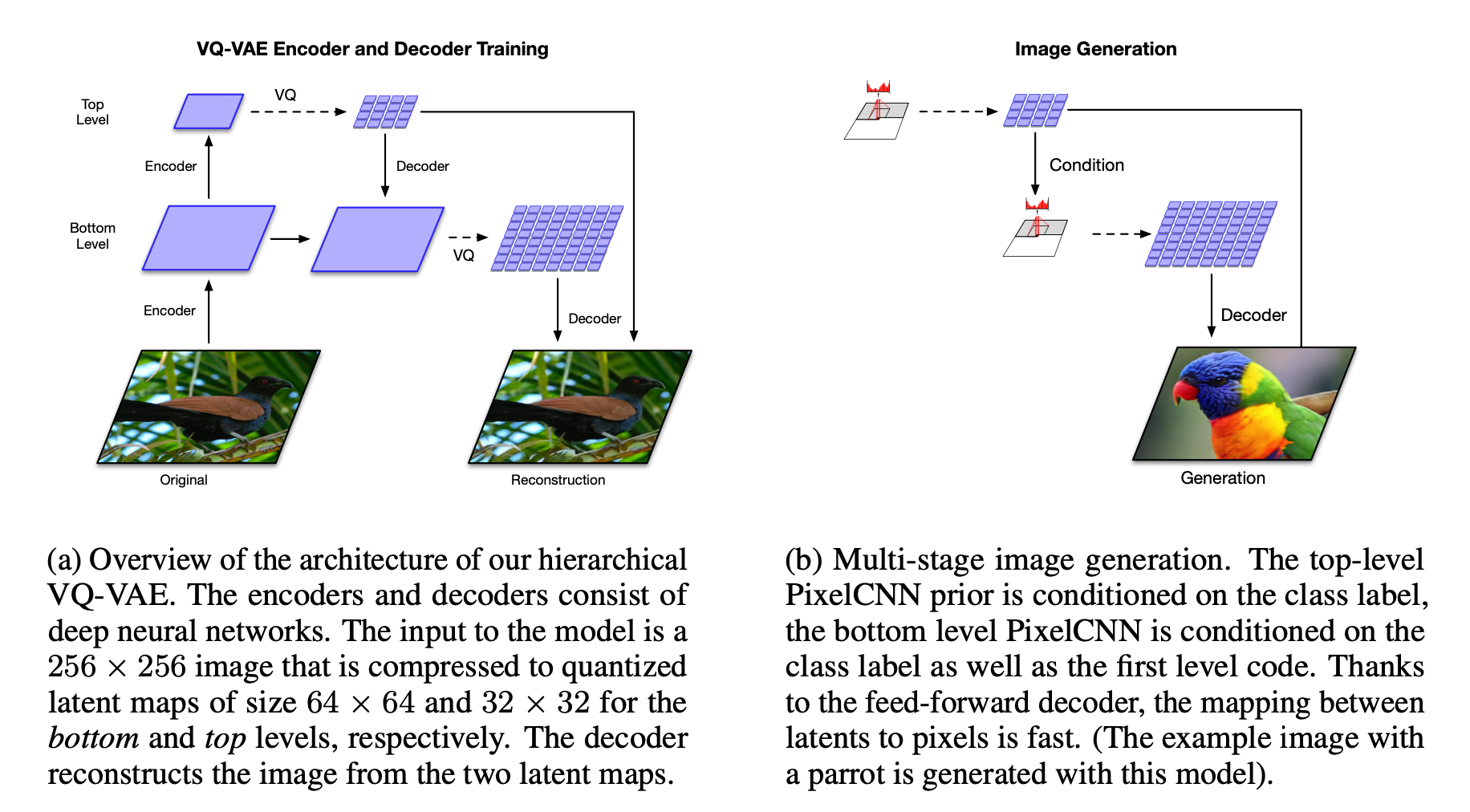
上图右边是生成新图片的过程。与之前的VQ-VAE不同的地方在于这里使用了双层结构。左边的 VQ-VAE 训练完成之后，对所有输入图片计算量子化的上层 $e_{top}$ 与下层 $e_{bottom}$, 将计算得到的 $\{e_{top}\}$ 和 $\{e_{bottom}\}$集合作为训练数据，训练 PixelCNN 神经网络，从而得到全局语义信息的联合概率密度 $p_{top}$ 和局部贴图信息的条件概率率密度 $p_{bottom}$。最后的生成过程是从 $p_{top}$ 和 $p_{bottom}$ 抽样得到量子化的字典向量，输入解码器，生成新的图片。$p_{top}$保证全局自洽，$p_{bottom}$保证局部高清。

原始的 VQ-VAE 使用自回归神经网络学习 $z$ 的序列分布。在 VQ-VAE-2 中，对上层 $\{e_{top}\}$，作者使用了多头自注意力机制（multi-headed self-attention ）。自注意力机制因为考虑了任何一个位置与其他所有位置的关联，有比较好的长程关联。但因为计算复杂度是 $O(n^2)$, 对于底层 feature map，n=64x64，显存溢出，所以在实际计算中，只对上层使用全局注意力机制。来自顶层的条件概率可以帮助底层生成很好的局部贴图。详细流程如下：

总结

到此，总算把VQ-VAE用自己认为比较好的方式讲清楚了。纵观全文，其实没有任何VAE的味道，所以我说它其实就是一个AE，一个编码为离散型向量的AE。它能重构出比较清晰的图像，则是因为它编码时保留了足够大的feature map.

如果弄懂了VQ-VAE，那么它新出的2.0版本也就没什么难理解的了，VQ-VAE-2相比VQ-VAE几乎没有本质上的技术更新，只不过把编码和解码都分两层来做了（一层整体，一层局部），从而使得生成图像的模糊感更少（相比至少是少很多了，但其实你认真看VQ-VAE-2的大图，还是有略微的模糊感的）。

不过值得肯定的是，VQ-VAE整个模型还是挺有意思，离散型编码、用Straight-Through的方法为梯度赋值等新奇特点，非常值得我们认真学习，能加深我们对深度学习的模型和优化的认识（梯度你都能设计了，还担心设计不好模型吗？）。

Reference

VQ-VAE的简明介绍：量子化自编码器

VQ-VAE解读