扩散模型的物理背景

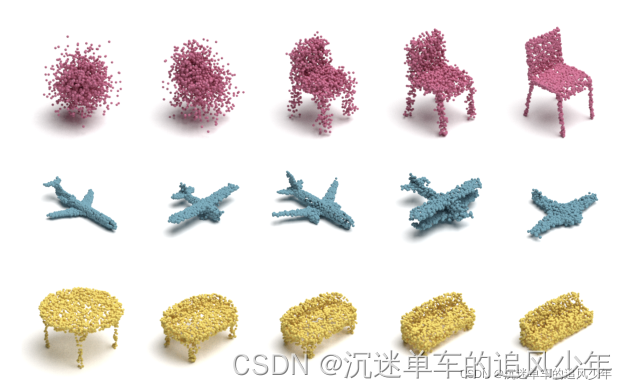
点云扩散过程

初中化学/物理就学过扩散运动，布朗运动就是一种典型的扩散过程。如果你忘了，可以复习复习：

布朗运动是指悬浮在液体或气体中的微粒所做的永不停息的无规则运动。其因由英国植物学家布朗所发现而得名。作布朗运动的微粒的直径一般为 10-5~10-3 厘米，这些小的微粒处于液体或气体中时，由于液体分子的热运动，微粒受到来自各个方向液体分子的碰撞，当受到不平衡的冲撞时而运动，由于这种不平衡的冲撞，微粒的运动不断地改变方向而使微粒出现不规则的运动。布朗运动的剧烈程度随着流体的温度升高而增加。

刚才说的物理背景，重点就是：这是一种从有序到无序的过程。在深度学习中，什么是最典型的无序？没错，就是噪声。

除此之外，这种有序和无序之间的转换，在生成模型中大有用处。理论上任何生成模型都能应用到，例如三维点云的生成、语音的生成、视频的生成、图片的生成。

应用领域

图像生成、图像分割、音频建模、自然语言处理、时间序列预测、点云重建等

音频生成DiffWave: A Versatile Diffusion Model for Audio Synthesis PriorGrad: Improving Conditional Denoising Diffusion Models with Data-Driven Adaptive PriorBDDM: Bilateral Denoising Diffusion Models for Fast and High-Quality Speech SynthesisItô-Taylor Sampling Scheme for Denoising Diffusion Probabilistic Models using Ideal DerivativesDenoising Diffusion Gamma ModelsCRASH: Raw Audio Score-based Generative Modeling for Controllable High-resolution Drum Sound SynthesisDiffSinger: Singing Voice Synthesis via Shallow Diffusion MechanismGrad-TTS: A Diffusion Probabilistic Model for Text-to-SpeechWaveGrad: Estimating Gradients for Waveform Generation
音频增强Conditional Diffusion Probabilistic Model for Speech EnhancementA Study on Speech Enhancement Based on Diffusion Probabilistic ModelRestoring degraded speech via a modified diffusion modelNU-Wave: A Diffusion Probabilistic Model for Neural Audio Upsampling
时间序列预测Autoregressive Denoising Diffusion Models for Multivariate Probabilistic Time Series ForecastingCSDI: Conditional Score-based Diffusion Models for Probabilistic Time Series ImputationAutoregressive Denoising Diffusion Models for Multivariate Probabilistic Time Series Forecasting
三维点云重建Diffusion Probabilistic Models for 3D Point Cloud GenerationScore-Based Point Cloud DenoisingA Conditional Point Diffusion-Refinement Paradigm for 3D Point Cloud Completion
图像生成：https://arxiv.org/abs/2006.11239 https://arxiv.org/abs/2105.05233Perception Prioritized Training of Diffusion ModelsGenerating High Fidelity Data from Low-density Regions using Diffusion ModelsDiffusion Models for Counterfactual ExplanationsConditional Simulation Using Diffusion Schrödinger Bridges
模型改进Progressive Distillation for Fast Sampling of Diffusion Models | OpenReviewINNF+: Invertible Neural Networks, Normalizing Flows, and Explicit Likelihood Models
图像分割Diffusion Models for Implicit Image Segmentation EnsemblesLabel-Efficient Semantic Segmentation with Diffusion ModelsSegDiff: Image Segmentation with Diffusion Probabilistic Models
自然语言处理Zero-Shot Translation using Diffusion Models
图像分割DiffuseMorph: Unsupervised Deformable Image Registration Along Continuous Trajectory Using Diffusion ModelsSegDiff: Image Segmentation with Diffusion Probabilistic ModelsLabel-Efficient Semantic Segmentation with Diffusion Models
图像翻译(image-to-image)The Swiss Army Knife for Image-to-Image Translation: Multi-Task Diffusion ModelsDual Diffusion Implicit Bridges for Image-to-Image TranslationDenoising Diffusion Restoration ModelsDiffuseMorph: Unsupervised Deformable Image Registration Along Continuous Trajectory Using Diffusion ModelsConditional Image Generation with Score-Based Diffusion Models
想了解最新最全的 Diffusion Models 相关论文请看这篇博客：

学习扩散模型的预备知识

有不少订阅我专栏的读者问 Diffusion Models 很深奥读不懂，需要先看一些什么知识打下基础？虽然 diffusion models 是一个非常前沿的工作，但肯定不是凭空产生的，背后涉及到非常多深度学习的知识，我将从配分函数、基于能量模型、马尔科夫链蒙特卡洛采样、得分匹配、比率匹配、降噪得分匹配、桥式采样、深度玻尔兹曼机等方面，摘取一些经典的知识点，供读者参考。请看下面的博文：

配分函数

无向模型

有向图模型为我们提供了一种描述结构化概率模型的语言。而另一种常见的语言则是无向模型，也被称为马尔可夫随机场或者是马尔可夫网络。就像它们的名字所说的那样，无向模型中所有的边都是没有方向的。

当存在很明显的理由画出每一个指向特定方向的箭头时，有向模型显然最适用。有向模型中，经常存在我们理解的具有因果关系以及因果关系有明确方向的情况。接力赛的例子就是一个这样的情况。之前运动员的表现会影响后面运动员的完成时间，而后面运动员却不会影响前面运动员的完成时间。

然而并不是所有情况的相互作用都有一个明确的方向关系。当相互的作用并没有本质性的指向，或者是明确的双向相互作用时，使用无向模型更加合适。

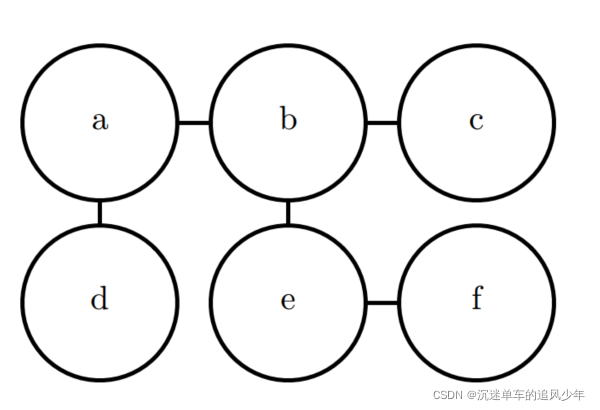
作为一个这种情况的例子，假设我们希望对三个二值随机变量建模：你是否生病，你的同事是否生病以及你的室友是否生病。就像在接力赛的例子中所作的简化假设一样，我们可以在这里做一些关于相互作用的简化假设。假设你的室友和同事并不认识，所以他们不太可能直接相互传染一些疾病，比如说感冒。这个事件太过罕见，所以我们不对此事件建模。然而，很有可能其中之一将感冒传染给你，然后通过你再传染给了另一个人。我们通过对你的同事传染给你以及你传染给你的室友建模来对这种间接的从你的同事到你的室友的感冒传染建模。

在这种情况下，你传染给你的室友和你的室友传染给你都是非常容易的，所以模型不存在一个明确的单向箭头。这启发我们使用无向模型。 其中随机变量对应着图中的相互作用的结点。与有向模型相同的是，如果在无向模型中的两个结点通过一条边相连接，那么对应这些结点的随机变量相互之间是直接作用的。不同于有向模型，在无向模型中的边是没有方向的，并不与一个条件分布相关联。

我们把对应你健康状况的随机变量记作 $h_y$，对应你的室友健康状况的随机变量记作$h_c$，你的同事健康的变量记作$h_c$。下图表示这种关系。

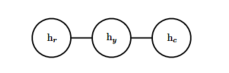
正式地说，一个无向模型是一个定义在无向模型 G上的结构化概率模型。对于图中的每一个团，一个因子$\phi$(也称为团势能)，衡量了团中变量每一种可能的联合状态所对应的密切程度。这些因子都被限制为是非负的。它们一起定义了未归一化概率函数：

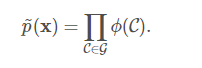
只要所有团中的结点数都不大，那么我们就能够高效地处理这些未归一化概率函数。它包含了这样的思想，密切度越高的状态有越大的概率。然而，不像贝叶斯网络，几乎不存在团定义的结构，所以不能保证把它们乘在一起能够得到一个有效的概率分布。下图展示了一个从无向模型中读取分解信息的例子。

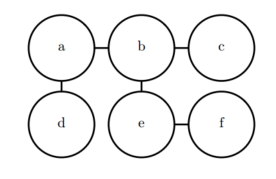
在你、你的室友和同事之间感冒传染的例子中包含了两个团。一个团包含了$h_y$和 $h_c$。这个团的因子可以通过一个表来定义，可能取到下面的值：状态为1代表了健康的状态，相对的状态为0则表示不好的健康状态（即感染了感冒）。你们两个通常都是健康的，所以对应的状态拥有最高的密切程度。两个人中只有一个人是生病的密切程度是最低的，因为这是一个很罕见的状态。两个人都生病的状态（通过一个人来传染给了另一个人）有一个稍高的密切程度，尽管仍然不及两个人都健康的密切程度。为了完整地定义这个模型，我们需要对包含$h_y$和$h_r$的团定义类似的因子。

配分函数

尽管这个未归一化概率函数处处不为零，我们仍然无法保证它的概率之和或者积分为1。为了得到一个有效的概率分布，我们需要使用对应的归一化的概率分布，一个通过归一化团势能乘积定义的分布也被称作是吉布斯分布：

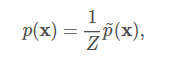
其中，Z是使得所有的概率之和或者积分为1的常数，并且满足：

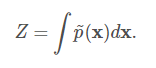
当函数p(x)固定时，我们可以把Z当成是一个常数。值得注意的是如果函数p(x)带有参数时，那么Z是这些参数的一个函数。在相关文献中为了节省空间忽略控制Z的变量而直接写Z是一个常用的方式。归一化常数Z被称作是配分函数，这是一个从统计物理学中借鉴的术语。

由于Z通常是由对所有可能的x状态的联合分布空间求和或者求积分得到的，它通常是很难计算的。为了获得一个无向模型的归一化概率分布，模型的结构和函数

的定义通常需要设计为有助于高效地计算Z。在深度学习中，Z通常是难以处理的。由于Z难以精确地计算出，我们只能使用一些近似的方法。

在设计无向模型时，我们必须牢记在心的一个要点是设定一些使得Z不存在的因子也是有可能的。当模型中的一些变量是连续的，且在其定义域上的积分发散时这种情况就会发生。例如，当我们需要对一个单独的标量变量建模，并且单个团势能在这种情况下，

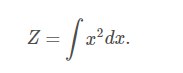
由于这个积分是发散的，所以不存在一个对应着这个势能函数的概率分布。有时候$\phi$函数某些参数的选择可以决定相应的概率分布是否能够被定义。参数$\beta$ 决定了归一化常数Z是否存在。正的$\beta$ 使得$\phi$函数是一个关于x的高斯分布，但是非正的参数$\beta$则使得$\phi$不可能被归一化。有向建模和无向建模之间一个重要的区别就是有向模型是通过从起始点的概率分布直接定义的，反之无向模型的定义显得更加宽松，通过$\phi$ 函数转化为概率分布而定义。这改变了我们处理这些建模问题的直觉。当我们处理无向模型时需要牢记一点，每一个变量的定义域对于一系列给定的 $\phi$ 函数所对应的概率分布有着重要的影响。举个例子，我们考虑一个n维向量的随机变量x以及一个由偏置向量b参数化的无向模型。假设x的每一个元素对应着一个团，并且满足$\phi^{(i)}(x_i)=exp(b_ix_i)$。在这种情况下概率分布是怎样的呢？答案是我们无法确定，因为我们并没有指定x的定义域。

能量模型和受限玻尔兹曼机

基于能量模型的定义

无向模型中许多有趣的理论结果都依赖于$\forall x, \tilde{p}(x)>0$ 这个假设。使这个条件满足的一种简单方式是使用基于能量的模型，其中：

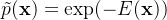
$E(x)$被称作是能量函数。对所有的$z, exp(z)$都是正的，这保证了没有一个能量函数会使得某一个状态x的概率为0。我们可以完全自由地选择那些能够简化学习过程的能量函数。如果我们直接学习各个团势能，我们需要利用约束优化方法来任意地指定一些特定的最小概率值。学习能量函数的过程中，我们可以采用无约束的优化方法。基于能量的模型中的概率可以无限趋近于0但是永远达不到0。

服从上式形式的任意分布都是玻尔兹曼分布的一个实例。正是基于这个原因，我们把许多基于能量的模型称为玻尔兹曼机。 关于什么时候称之为基于能量的模型，什么时候称之为玻尔兹曼机不存在一个公认的判别标准。 一开始玻尔兹曼机这个术语是用来描述一个只有二值变量的模型，但是如今许多模型，比如均值-协方差RBM，也涉及到了实值变量。虽然玻尔兹曼机最初的定义既可以包含潜变量也可以不包含潜变量，但是时至今日玻尔兹曼机这个术语通常用于指拥有潜变量的模型，而没有潜变量的玻尔兹曼机则经常被称为马尔可夫随机场或对数线性模型。

无向模型中的团对应于未归一化概率函数中的因子。通过$ exp(a+b) = exp(a) exp(b)$，我们发现无向模型中的不同团对应于能量函数的不同项。换句话说，基于能量的模型只是一种特殊的马尔可夫网络：求幂使能量函数中的每个项对应于不同团的一个因子。人们可以将能量函数中带有多个项的基于能量的模型视作是专家之积~{cite?}。能量函数中的每一项对应的是概率分布中的一个因子。能量函数中的每一项都可以看作决定一个特定的软约束是否能够满足的”专家”。每个专家只执行一个约束，而这个约束仅仅涉及随机变量的一个低维投影，但是当其结合概率的乘法时，专家们一同构造了复杂的高维约束。

基于能量的模型定义的一部分无法用机器学习观点来解释：即”-“符号。这个”-“符号可以被包含在E的定义之中。对于很多E函数的选择来说，学习算法可以自由地决定能量的符号。这个负号的存在主要是为了保持机器学习文献和物理学文献之间的兼容性。概率建模的许多研究最初都是由统计物理学家做出的，其中E是指实际的、物理概念的能量，没有任何符号。诸如”能量”和”配分函数”这类术语仍然与这些技术相关联，尽管它们的数学适用性比在物理中更宽。一些机器学习研究者发出了不同的声音，但这些都不是标准惯例。

许多对概率模型进行操作的算法不需要计算$p_{model(x)}$，而只需要计算$log \tilde{p}_{model}(x)$。对于具有潜变量 h的基于能量的模型，这些算法有时会将该量的负数称为自由能：

\[ \mathcal{F}(\boldsymbol{x})=-\log \sum_{\boldsymbol{h}} \exp (-E(\boldsymbol{x}, \boldsymbol{h})) \]

一般更倾向于更为通用的基于$log \tilde{p}_{model}(x)$的定义。

基于能量的学习为许多概率和非概率的学习方法提供了一个统一的框架，特别是图模型和其他结构化模型的非概率训练。基于能量的学习可以被看作是预测、分类或决策任务的概率估计的替代方法。由于不需要适当的归一化，基于能量的方法避免了概率模型中与估计归一化常数相关的问题。此外，由于没有标准化条件，在学习机器的设计中允许了更多的灵活性。大多数概率模型都可以看作是特殊类型的基于能量的模型，其中能量函数满足一定的归一化条件，损失函数通过学习优化，具有特定的形式。

用分类器做一个简单例子，如果输入是猫的图片，那么$E\left(x, \text { label }=^{\prime} c a t^{\prime}\right)=0$，即分类正确能量函数即为0，所以这里的能量函数其实与损失函数没有太大差别，可能是最大化数据的负对数似然。为了最小化这个能量，我们可以改变label使其适应（传统的图像分类），也可以改变来适应label。
GAN：判别器本身是一个能量函数，真实样本的能量为0。生成器尝试着生成能量更低的样本。
Self-supervised：比如我们要从当前帧预测下一帧内容，那么我们需要找到一个$E\left(x^{t}, x^{t+1}\right)$帧使得能量尽可能小即可。

受限玻尔兹曼机

受限玻尔兹曼机或者簧风琴是图模型如何用于深度学习的典型例子。 RBM~本身不是一个深层模型。相反，它有一层潜变量，可用于学习输入的表示。我们将看到RBM如何被用来构建许多的深层模型。在这里，举例展示RBM在许多深度图模型中使用的实践：它的单元被分成很大的组，这种组称作层，层之间的连接由矩阵描述，连通性相对密集。该模型被设计为能够进行高效的吉布斯采样，并且模型设计的重点在于以很高的自由度来学习潜变量，而潜变量的含义并不是设计者指定的。之后将更详细地再次讨论RBM。

标准的RBM是具有二值的可见和隐藏单元的基于能量的模型。其能量函数为：

\[ E(\boldsymbol{v}, \boldsymbol{h})=-\boldsymbol{b}^{\top} \boldsymbol{v}-\boldsymbol{c}^{\top} \boldsymbol{h}-\boldsymbol{v}^{\top} \boldsymbol{W h} \]

其中b,c和W都是无约束、实值的可学习参数。我们可以看到，模型被分成两组单元：v和h，它们之间的相互作用由矩阵W来描述。该模型在下图中以图的形式描绘。该图能够使我们更清楚地发现，该模型的一个重要方面是在任何两个可见单元之间或任何两个隐藏单元之间没有直接的相互作用（因此称为”受限”，一般的玻尔兹曼机可以具有任意连接）。

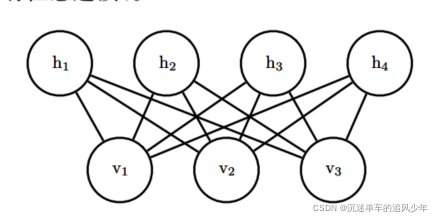
对 RBM 结构的限制产生了良好的属性：

\[ \begin{aligned} &p(\mathbf{h} \mid \mathbf{v})=\prod_{i} p\left(\mathrm{~h}_{i} \mid \mathbf{v}\right) \\ &p(\mathbf{v} \mid \mathbf{h})=\prod_{i} p\left(\mathbf{v}_{i} \mid \mathbf{h}\right) \end{aligned} \]

独立的条件分布很容易计算。对于二元的受限玻尔兹曼机，我们可以得到：

\[ \begin{aligned} &p\left(\mathrm{~h}_{i}=1 \mid \mathbf{v}\right)=\sigma\left(\mathbf{v}^{\top} \boldsymbol{W}_{:, i}+b_{i}\right) \\ &p\left(\mathrm{~h}_{i}=0 \mid \mathbf{v}\right)=1-\sigma\left(\mathbf{v}^{\top} \boldsymbol{W}_{:, i}+b_{i}\right) \end{aligned} \]

结合这些属性可以得到高效的块吉布斯采样（block Gibbs Sampling），它在同时采样所有 h 和同时采样所有 v 之间交替。

由于能量函数本身只是参数的线性函数，很容易获取能量函数的导数。例如：

\[ \frac{\partial}{\partial W_{i, j}} E(\mathbf{v}, \mathbf{h})=-\mathbf{v}_{i} \mathbf{h}_{j} \]

训练模型可以得到数据v的表示h。我们经常使用$\mathbb{E}_{\mathbf{h} \sim p(\mathbf{h} \mid v)}[\boldsymbol{h}]$作为一组描述v的特征。

总的来说，RBM展示了典型的图模型深度学习方法： 使用多层潜变量，并由矩阵参数化层之间的高效相互作用来完成表示学习。

图模型为描述概率模型提供了一种优雅、灵活、清晰的语言。

蒙特卡洛采样法和重要采样法

蒙特卡洛采样法

蒙特卡洛原来是一个赌场的名称，用它作为名字大概是因为蒙特卡洛方法是一种随机模拟的方法，这很像赌博场里面的扔骰子的过程。最早的蒙特卡洛方法都是为了求解一些不太好求解的求和或者积分问题。

例如下图是一个经典的用蒙特卡洛求圆周率的问题，用计算机在一个正方形之中随机的生成点，计数有多少点落在1/4圆之中，这些点的数目除以总的点数目即圆的面积，根据圆面积公式即可求得圆周率：

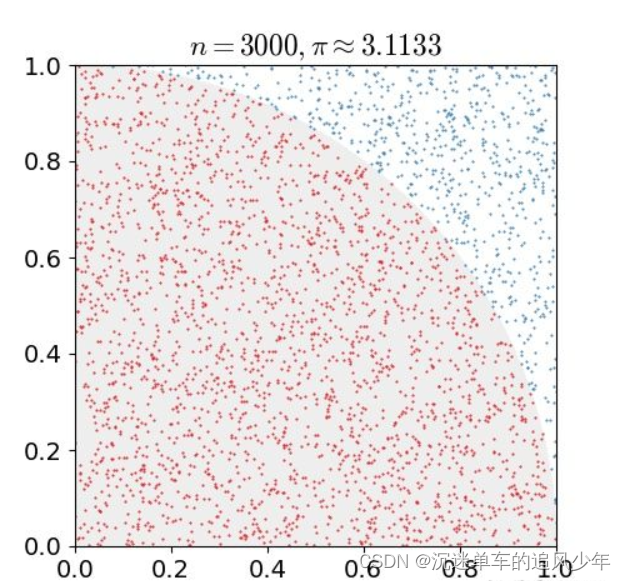
蒙特卡洛算法的另一个应用是求积分，某些函数的积分不好求，我们可以按照下面的方法将这个函数进行分解，之后转化为求期望与求均值的问题：

\[ \int_{a}^{b}h(x)dx=\int_{a}^{b}f(x)p(x)dx=E_{p(x)}[f(x)]\\ E_{p(x)}[f(x)]=\frac{1}{n}\sum_i f(x_i) \]

最终使用蒙特卡洛的方法求得积分。

对某一种概率分布p(x)进行蒙特卡洛采样的方法主要分为直接采样法、拒绝采样法与重要采样法三种：

直接采样法
直接采样的方法是根据概率分布进行采样。对一个已知概率密度函数与累积概率密度函数的概率分布，我们可以直接从累积分布函数（cdf）进行采样

如下图所示是高斯分布的累积概率分布函数，可以看出函数的值域是(0, 1)，我们可以从U(0, 1)均匀分布中进行采样，再根据累积分布函数的反函数计算对应的x，这样就获得了符合高斯分布的N个粒子：

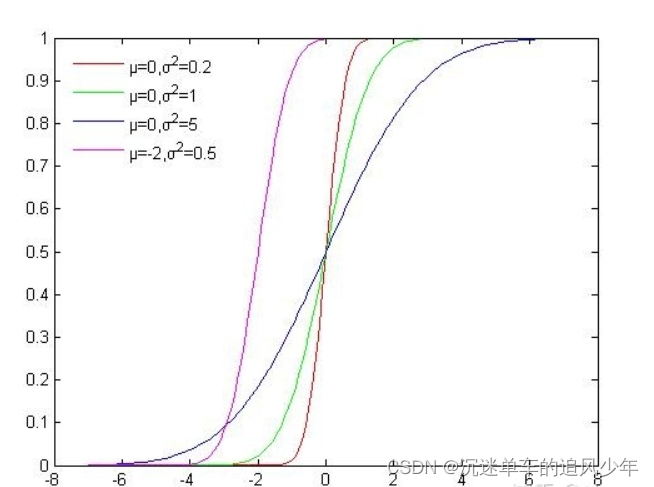
使用累积分布函数进行采样看似简单，但是由于很多分布我们并不能写出概率密度函数与累积分布函数，所以这种方法的适用范围较窄。

接受拒绝采样法
对于累积分布函数未知的分布，我们可以采用接受-拒绝采样。如下图所示，p(z)是我们希望采样的分布，q(z)是我们提议的分布(proposal distribution)，令kq(z)>p(z)，我们首先在kq(z)中按照直接采样的方法采样粒子，接下来判断这个粒子落在途中什么区域，对于落在灰色区域的粒子予以拒绝，落在红线下的粒子接受，最终得到符合p(z)的N个粒子。