INCOMING TRANSMISSION

LATEST UPDATES
ALL WIP FAV

三维中旋转的表示方式--欧拉角、旋转矩阵、旋转向量、四元数

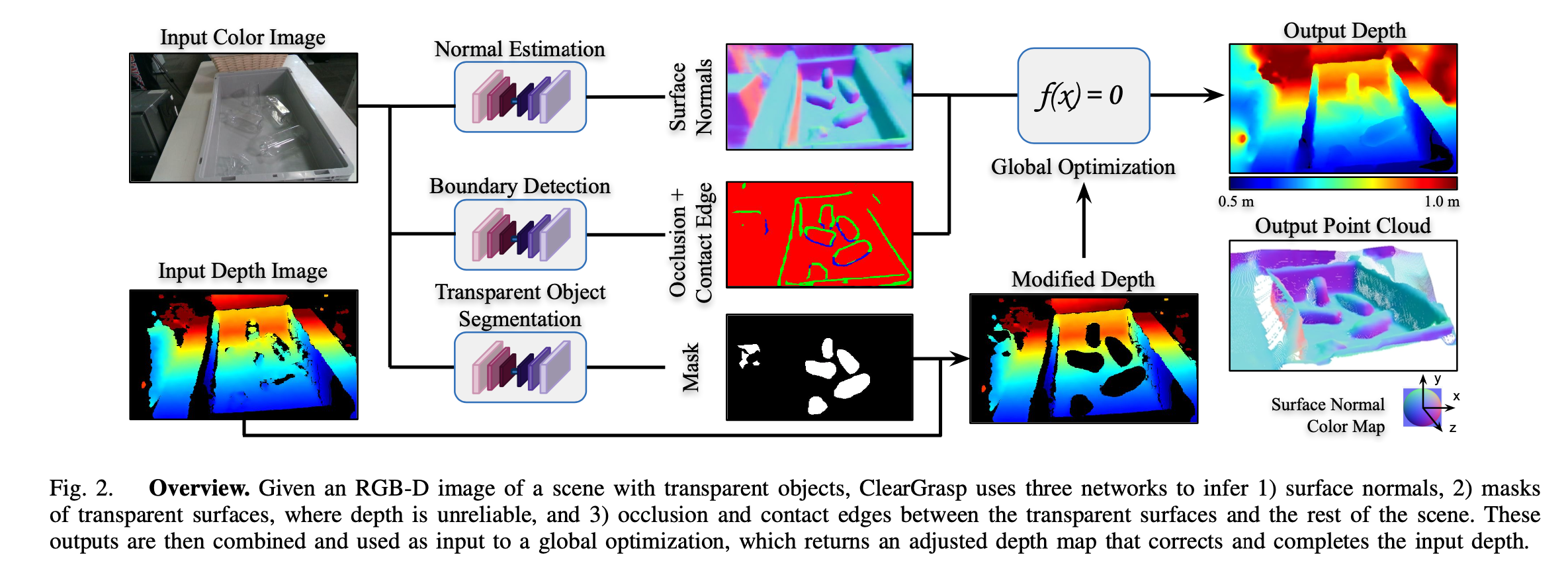
3D Model
2024-12-31
三维空间中的旋转有很多种表示方式，欧拉角，旋转矩阵，旋转向量，四元数。由于在slam与机器人中会大量用到这方面的知识，所以在这里将此方面的知识总结一下，方便以后查阅。 欧拉角（Euler Angle） 欧拉角可以使用滑翔翼飞行器控制来理解，比如对于下面这张图，一般假设红色轴为z轴，则z轴表示空间的第三维，则去掉这一维度表示飞行器在一个二维平面上；蓝色轴为x轴，也是飞行器的朝向，因此绕此轴转动就像是飞行器在做翻滚动作，因此叫翻滚角（roll）；绿色轴为y轴，绕这个轴转动其实就是飞机开始准备向上飞或者向下飞了，因此叫俯仰角（pitch）；同理，绕红色轴也就是z轴转动代表飞机开始调整自身在二维平面上的朝向了，因此叫偏航角（yaw）。 在欧拉角的表示中，yaw、pitch、roll的顺序对旋转结果是...
#3D
READ

SO-Net

3D Model
2024-12-31
概括 针对一些网络在处理point cloud时的缺点，如：不能对点的空间分布进行建模（例如PointNet++，只是能获取局部信息不能得到局部区域之间的空间关系），提出了SONet。SO的含义是利用Selforganizing map的Net。 结果：它具有能够对点的空间分布进行建模、层次化特征提取、可调节的感受野范围的优点，并能够用于多种任务如重建、分类、分割等等。取得了相似或超过SOTA的性能，因为可并行化和架构简单使得训练速度很快。 贡献： TODO IDEA：作者发现将CNN直接用于SOM图上性能不升反降，为什么（推测：可能是SOM的2D map并不是保持了原本的空间对应关系，可能nodes之间是乱序的，导致用conv2d时精度反而降低）？ 难点 如何对local regions之...
#3D
READ

VoteNet

3D Model
2024-12-31
Hough Voting 本文的标题是Deep Hough Voting，先来说一下Hough Voting。 用Hough变换检测直线大家想必都听过：对于一条直线，可以使用(r, θ)两个参数进行描述，那么对于图像中的一点，过这个点的直线有很多条，可以生成一系列的(r, θ)，在参数平面内就是一条曲线，也就是说，一个点对应着参数平面内的一个曲线。那如果有很多个点，则会在参数平面内生成很多曲线。那么，如果这些点是能构成一条直线的，那么这条直线的参数(r, θ)就在每条曲线中都存在，所以看起来就像是多条曲线相交在（r,θ）。可以用多条曲线投票的方式来看，其他点都是很少的票数，而（r,θ）则票数很多，所以直线的参数就是（r,θ）。 所以Hough变换的思想就是在于，在参数空间内进行投票，投票得数...
#3D
READ

PointConv

3D Model
2024-12-31
概括 这篇文章将卷积比较自然地拓展到点云的情形，思路很赞！ 文章的主要创新点：“weight function”和“density function”，并能实现translationinvariance和permutationinvariance，可以实现层级化特征提取，而且能自然推广到其deconvolution的情形实现分割，在二维CIFAR10图像分类任务中精度堪比CNN（表明能够充分近似卷积网络），达到了SOTA的性能。 缺点：每个kernel都需要由“kernel function”生成，而“kernel function”实质上是一个CNN网络，计算量比较大。 思想 察觉到：二维卷积中pixel的相对centroid位置与kernel vector的生成方式有关。 以二维卷积为例...
#3D
READ

PointNet系列

3D Model
2024-12-31
三维深度学习简介 多视角（multiview）：通过多视角二维图片组合为三维物体，此方法将传统CNN应用于多张二维视角的图片，特征被view pooling procedure聚合起来形成三维物体； 体素（volumetric）：通过将物体表现为空间中的体素进行类似于二维的三维卷积（例如，卷积核大小为5x5x5），是规律化的并且易于类比二维的，但同时因为多了一个维度出来，时间和空间复杂度都非常高，目前已经不是主流的方法了； 点云（point clouds）：直接将三维点云抛入网络进行训练，数据量小。主要任务有分类、分割以及大场景下语义分割； 非欧式（manifold，graph）：在流形或图的结构上进行卷积，三维点云可以表现为mesh结构，可以通过点对之间临接关系表现为图的结构。 点云的特性...
#3D
READ

ManyDepth

3D Model
2024-12-31
引言 常用的自监督深度估计方法常使用（1）单帧信息；（2）多帧信息（视频序列），来预测输入图片的深度。本文提出的深度估计方法是基于视频序列的深度估计方法。 在基于视频序列的深度估计方法中，传统方法（比如ORB SLAM等）通过相邻帧的特征匹配来得到对应的特征点，通过特征点的对应关系来估计相机位姿变换，同时获得特征点的深度信息，这本身就是无监督的方法。 而自监督深度学习中，我们常通过两个网络（1）深度网络；（2）位姿网络，来同时得到相邻帧的深度和相机位姿信息，然后通过精心设计的损失函数使两个网络完成自洽并收敛。这达到了一种端到端的训练，我们只需要简单地将视频序列和一些必要的参数（比如相机内参 K ）输入网络，即可完成训练。 经过上述描述，我们可以意识到，在基于视频序列的深度估计方法中上下文信息...
#3D
READ

深度图补全

3D Model
2024-12-31
概述 虽然RGBD相机前景无限，但是受制于物理硬件的限制，目前深度相机输出的depth图还有很多问题，比如对于光滑物体表面反射、半/透明物体、深色物体、超出量程等都会造成深度图缺失。而且很多深度相机是大片的深度值缺失，这对于算法工程师来说非常头疼。 因此，深度图补全一直是一个非常有用的研究方向，之前的文献大都只能补全比较小范围的深度缺失，对于较大深度值缺失的情况无能无力，本文介绍的是2018 CVPR 最新的一项研究deep depth completion，不受RGBD相机类型的限制，只需要输入一张RGB加一张depth图，可以补全任意形式深度图的缺失。对于算法工程师来说真的是喜大普奔啊，目前主要针对的是室内环境。 数据集 本文引入新数据集，基于Matterport3D数据集重新构建完整的...
#3D
READ

DPANet

3D Model
2024-12-31
摘要 DPANet: Depth PotentialityAware Gated Attention Network for RGBD Salient Object Detection 在RGBD显著目标检测中，主要存在两个问题： 1. 如何有效地整合跨模态RGBD数据的互补性 1. 如何防止不可靠深度图的污染效应。 实际上，这两个问题是相互联系、相互交织的，但以往的方法往往只关注第一个问题，而忽略了对深度图质量的考虑，这可能导致模型陷入次优状态。在本文中，我们在一个整体模型中协同地解决这两个问题，并提出了一个新的网络DPANet来显式地建模深度图的潜力并有效地整合跨模态互补性。通过引入深度潜势感知，网络能够以学习的方式感知深度信息的潜势，指导两模态数据的融合过程，防止污染的发生。融合过程中...
#3D
READ

ClearGrasp

3D Model
2024-12-31
简介 对于标准的3D传感器来说，扫描透明物体一直是个难题，传统的双目，结构光或ToF RGBD镜头都对透明物体束手无策，它们难以产生准确的深度估计，通常在许多情况下，透明物体会显示为一堆无效的噪点或失真的近似平面，如下图。谷歌+Synthesis AI+哥伦比亚大学的研究团队推出了ClearGrasp技术，通过深度学习的引入增强识别和估计透明物体。 为什么3D镜头无法对透明物体呈像，原因是传统3D传感器的算法会假定所以物体的表面都符合完全漫反射（Lambertian)。即所有方向上的反光都是均匀的，然而透明物体却不符合这个假设，不仅光存在反射，还存在折射。 三个关键点 RGBD相机通常对于典型的非透明物体表面，可以提供良好的深度估计。 因此，我们推测不必要从头开始直接估算所有几何图形深度，而...
#3D
READ

Softmax-based Loss的演化史

Computer Vision
2024-12-31
近期，人脸识别研究领域的主要进展之一集中在了 Softmax Loss 的改进之上；本文从两种主要的改进方式——做归一化以及增加类间 margin——展开梳理，介绍了近年来基于 Softmax 的 Loss 的研究进展。 Softmax简介 Softmax Loss 因为其易于优化，收敛快等特性被广泛应用于图像分类领域。然而，直接使用 softmax loss 训练得到的 feature 拿到 retrieval，verification 等“需要设阈值”的任务时，往往并不够好。 这其中的原因还得从 Softmax 的本身的定义说起，Softmax loss 在形式上是 softmax 函数加上交叉熵损失，它的目的是让所有的类别在概率空间具有最大的对数似然，也就是保证所有的类别都能分类正确，...
#人脸识别 #CV
READ

人脸识别Loss

Computer Vision
2024-12-31
超多分类的Softmax 2014年CVPR两篇超多分类的人脸识别论文：DeepFace和DeepID DeepFace Taigman Y, Yang M, Ranzato M A, et al. Deepface: Closing the gap to humanlevel performance in face verification [C]// CVPR, 2014. 4.4M训练集，训练6层CNN + 4096特征映射 + 4030类Softmax，综合如3D Aligement, model ensembel等技术，在LFW上达到97.35%。 DeepID Sun Y, Wang X, Tang X. Deep learning face representation fro...
#人脸识别 #CV
READ

A-Softmax

Computer Vision
2024-12-31
推导 回顾一下二分类下的Softmax后验概率，即： [公式] 显然决策的分界在当 𝑝_1=𝑝_2 时，所以决策界面是 (𝑊_1−𝑊_2)𝑥+𝑏_1−𝑏_2=0 。我们可以将 𝑊^𝑇_𝑖𝑥+𝑏_𝑖 写成 ‖W_i^T‖⋅‖x‖cos⁡(θ_i)+b_i ，其中 θ_i 是 W_i 与 x 的夹角，如对 W_i 归一化且设偏置 b_i 为零（ ‖W_i‖=1 ， b_i=0 ），那么当 p_1=p_2 时，我们有 cos⁡(θ_1)−cos⁡(θ_2)=0 。从这里可以看到，如里一个输入的数据特征 x_i 属于 𝑦_𝑖 类，那么 θ_{y_i} 应该比其它所有类的角度都要小，也就是说在向量空间中 W_{y_i} 要更靠近 x_i 。 我们用的是Softmax Loss，对于输入 x_i ，So...
#人脸识别 #CV
READ
1 ... 14 15 16 17 18 ... 24