推导
回顾一下二分类下的Softmax后验概率,即:
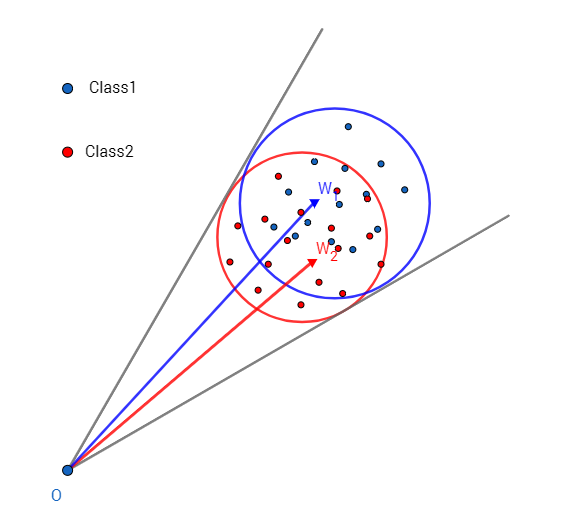
显然决策的分界在当 \(𝑝_1=𝑝_2\)时,所以决策界面是\((𝑊_1−𝑊_2)𝑥+𝑏_1−𝑏_2=0\)。我们可以将\(𝑊^𝑇_𝑖𝑥+𝑏_𝑖\) 写成 \(‖W_i^T‖⋅‖x‖cos(θ_i)+b_i\),其中 \(θ_i\)是\(W_i\) 与 \(x\)
的夹角,如对 \(W_i\) 归一化且设偏置 \(b_i\)为零(\(‖W_i‖=1\),\(b_i=0\)),那么当 \(p_1=p_2\)时,我们有\(cos(θ_1)−cos(θ_2)=0\)。从这里可以看到,如里一个输入的数据特征\(x_i\) 属于\(𝑦_𝑖\)类,那么 \(θ_{y_i}\) 应该比其它所有类的角度都要小,也就是说在向量空间中 \(W_{y_i}\) 要更靠近 \(x_i\)。
我们用的是Softmax Loss,对于输入\(x_i\),Softmax Loss\(L_i\)定义以下:
上式中的\(𝑗∈[1,𝐾]\),其中\(𝐾\) 类别的总数。上面我们限制了一些条件:\(‖𝑊_𝑖‖=1,𝑏_𝑖=0\),由这些条件,可以得到修正的损失函数(也就是论文中所以说的modified softmax loss):
在二分类问题中,当\(cos(\theta_1)>cos(\theta_2)\)时,可以确定属于类别1,但分类1与分类2的决策面相同,说明分类1与分类2之间的间隔(margin)相当小,直观上的感觉就是分类不明显。如果要让分类1与分类2有一个明显的间隔,可以做两个决策面,对于类别1的决策平面为:\(cos(m\theta_1)=cos(\theta_2)\),对于类别2的策平面为:\(cos(\theta_1)=cos(𝑚\theta_2)\),其中 \(𝑚≥2,𝑚∈𝑁\)。\(𝑚\) 是整数的目的是为了方便计算,因为可以利用倍角公式,\(𝑚≥2\) 说明与该分类的最大夹角要比其它类的小夹角还要小\(𝑚\) 倍。如果\(𝑚=1\) ,那么类别1与类别2的决策平面是同一个平面,如果\(𝑚≥2v\),那么类别1与类别2的有两个决策平面,相隔多大将会在性质中说明。从上述的说明与\(𝐿_{𝑚𝑜𝑑𝑖𝑓𝑖𝑒𝑑}\)可以直接得到A-Softmax Loss:
其中\(\theta_{𝑦_𝑖,𝑖}∈[0,\frac{\pi}{𝑚}]\),因为\(\theta_{𝑦_{𝑖,𝑖}}\)在这个范围之外可可能会使得\(m\theta_{y_i,i}>\theta_{j,i},j\neq y_i\)(这样就不属于分类\(𝑦_𝑖\)了),但\(cos(𝑚\theta_1)>cos(\theta_2)\)仍可能成立,而我们Loss方程用的还是\(cos(\theta)\)。为了避免这个问题,可以重新设计一个函数来替代\(cos(𝑚\theta_{𝑦_𝑖,𝑖})\),定义\(\psi(\theta_{y_i,i})=(-1)^k\cos(m\theta_{y_i,i})-2k\),其中\(\theta_{𝑦_𝑖,𝑖}∈[\frac{𝑘\pi}{𝑚},\frac{(𝑘+1)\pi}{𝑚}]\),且\(𝑘∈[1,𝑘]\)。这个函数的定义可以使得\(\psi\) 随\(\theta_{𝑦_𝑖,𝑖}\) 单调递减,如果\(m\theta_{y_i,i}>\theta_{j,i},j\neq y_i\), 那么必有\(\psi(\theta_{y_i,i})<\cos(\theta_{j,i})\),反而亦然,这样可以避免上述的问题,所以有:
对于以上三种二分类问题的Loss(多分类是差不多的情况)的决策面,可以总结如下表:
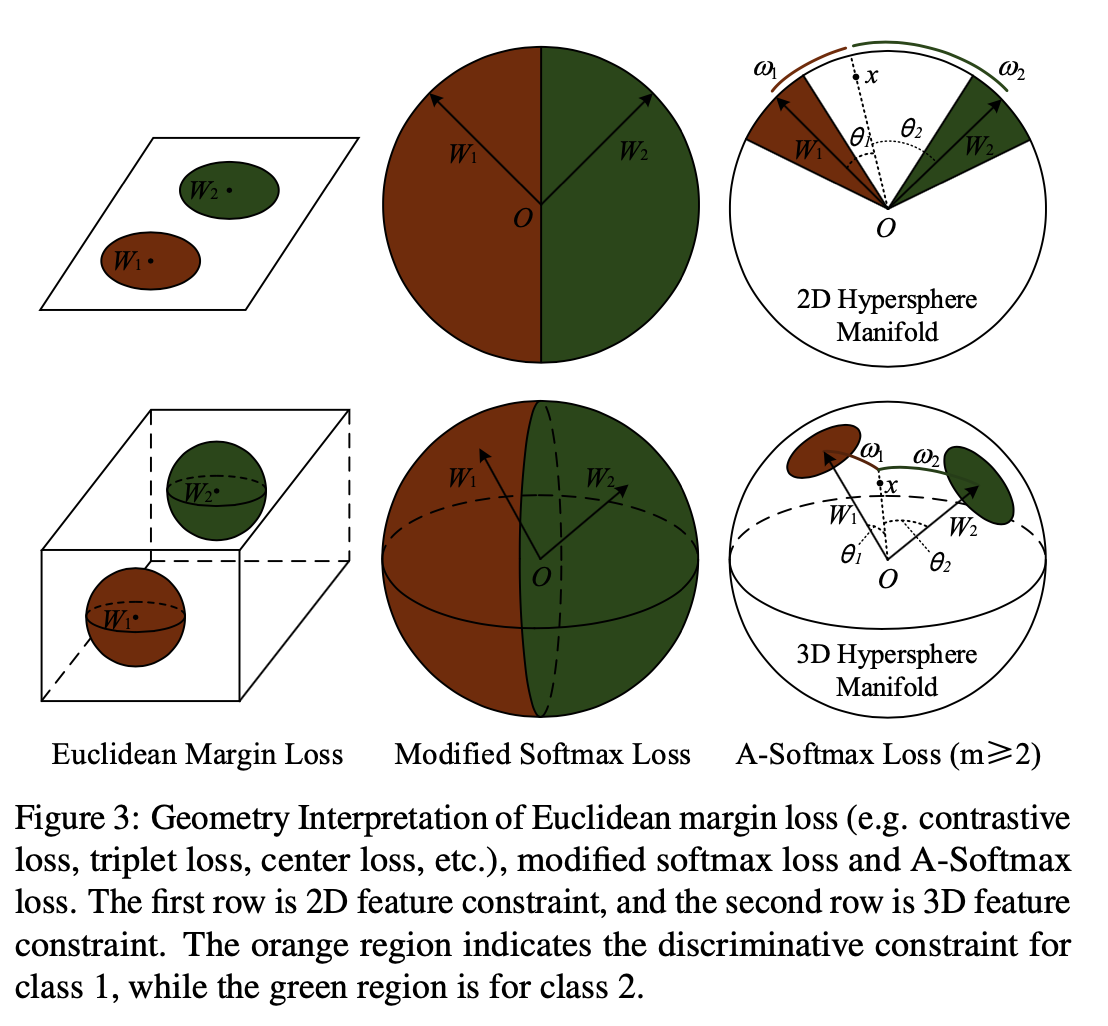
论文中还给出了这三种不同Loss的几何意义,可以看到的是普通的softmax(Euclidean Margin Loss)是在欧氏空间中分开的,它映射到欧氏空间中是不同的区域的空间,决策面是一个在欧氏空间中的平面,可以分隔不同的类别。Modified Softmax Loss与A-Softmax Loss的不同之处在于两个不同类的决策平面是同一个,不像A-Softmax Loss,有两个分隔的决策平面且决策平面分隔的大小还是与𝑚的大小成正相关,如下图所示。
A-Softmax Loss的性质
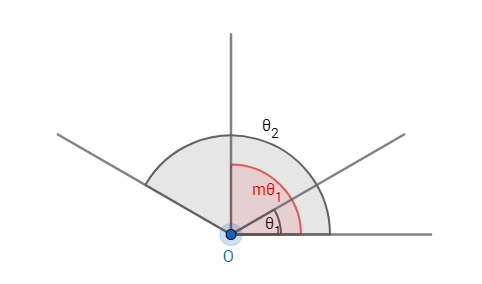
性质1:A-Softmax Loss定义了一个大角度间隔的学习方法,\(𝑚\) 越大这个间隔的角度也就越大,相应区域流形的大小就越小,这就导致了训练的任务也越困难。这个性质是相当容易理解的,如图1所示:这个间隔的角度为\((𝑚−1)\theta_1\) ,所以\(𝑚\) 越大,则间隔的角度就越小;同时\(𝑚\theta_1<\pi\),所以\(𝑚\) 越大,则相应的区域流形\(\theta_1\)就越小。
定义1:\(m_{min}\) 被定义为当 \(m>m_{min}\) 时有类内间的最大角度特征距离小于类间的最小角度特征距离。
性质2:
在二分类问题中:\(m_{min}>2+\sqrt{3}\),有多分类问题中:\(m_{min}≥3\)。证明参考这篇文章
A-Softmax的几何意义
个人认为A-Softmax是基于一个假设:不同的类位于一个单位超球表面的不同区域。从上面也可以知道它的几何意义是权重所代表的在单位超球表面的点,在训练的过程中,同一类的输入映射到表面上会慢慢地向中心点(这里的中心点大部分时候和权重的意义相当)聚集,而到不同类的权重(或者中心点)慢慢地分散开来。m的大小是控制同一类点聚集的程度,从而控制了不同类之间的距离。从下图可以看到,不同的m对映射分布的影响。

A-Softmax在较小的数据集合上有着良好的效果且理论具有不错的可解释性,它的缺点也明显就是计算量相对比较大,也许这就是作者在论文中没有测试大数据集的原因。
与L-Softmax的区别
A-Softmax与L-Softmax的最大区别在于A-Softmax的权重归一化了,而L-Softmax则没有。A-Softmax权重的归一化导致特征上的点映射到单位超球面上,而L-Softmax则没有这个限制,这个特性使得两者在几何的解释上是不一样的。如图所示,如果在训练时两个类别的特征输入在同一个区域时。A-Softmax只能从角度上分度这两个类别,也就是说它仅从方向上区分类,分类的结果如图所示;而L-Softmax,不仅可以从角度上区别两个类,还能从权重的模(长度)上区别这两个类,分类的结果如图所示。在数据集合大小固定的条件下,L-Softmax能有两个方法分类,训练可能没有使得它在角度与长度方向都分离,导致它的精确可能不如A-Softmax。