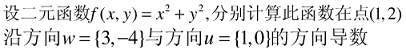INCOMING TRANSMISSION

LATEST UPDATES
ALL WIP FAV

逻辑回归(LR)

Machine Learning
2025-01-01
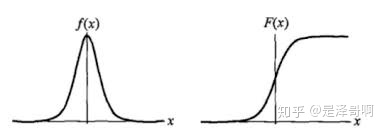
1. 模型介绍 Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。 Logistic 回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。 1.1 Logistic 分布 Logistic 分布是一种连续型的概率分布，其分布函数和密度函数分别为： [公式] 其中， [Math] 表示位置参数， [Math] 为形状参数。我们可以看下其图像特征： Logistic 分布是由其位置和尺度参数定义的连续分布。Logistic 分布的形状与正态分布的形状相似，但是 Logistic 分布的尾部更长，所以我们可以使用 Logistic 分布来建模比正态分布具...
#Machine Learning
READ

Kernel LR (核逻辑回归)

Machine Learning
2025-01-01
Kernel Logistic Regression 介绍如何将Kernel Trick引入到Logistic Regression，以及LR与SVM的结合 SVM与正则化 首先回顾SoftMargin SVM的原始问题: [公式] 其中 ξ_n 是训练数据违反边界的多少，没有违反的话， ξ_n=0 ，反之 ξ_n0 ，换句话说，目标函数的第二项就可以表示模型的损失。现在换一种方式来写，将二者结合起来: ξ_n=max(1−y_n(w^Tz^n+b),0) ，这一个等式就代表了上面的约束条件，这样上述问题，就与下面的无约束问题等价 [公式] 这种形式与之前的L2 正则项很类似: [公式] 在L2中，通过最小化 E_{in} 的同时控制 w 的大小，防止模型过度复杂。从正则化的角度来看的话，S...
#Machine Learning
READ

自组织映射网络（SOM）

Machine Learning
2025-01-01
什么是自组织映射？ 一个特别有趣的无监督系统是基于竞争性学习，其中输出神经元之间竞争激活，结果是在任意时间只有一个神经元被激活。这个激活的神经元被称为胜者神经元（winnertakesall neuron）。这种竞争可以通过在神经元之间具有横向抑制连接（负反馈路径）来实现。其结果是神经元被迫对自身进行重新组合，这样的网络我们称之为自组织映射（Self Organizing Map，SOM）。 拓扑映射 神经生物学研究表明，不同的感觉输入（运动，视觉，听觉等）以有序的方式映射到大脑皮层的相应区域。 这种映射我们称之为拓扑映射，它具有两个重要特性： 在表示或处理的每个阶段，每一条传入的信息都保存在适当的上下文（相邻节点）中 处理密切相关的信息的神经元之间保持密切，以便它们可以通过短突触连接进行交...
#Machine Learning
READ

L1正则化与L2正则化

Machine Learning
2025-01-01
正则化 正则化是一个通用的算法和思想，所以会产生过拟合现象的算法都可以使用正则化来避免过拟合。 在经验风险最小化的基础上（也就是训练误差最小化），尽可能采用简单的模型，可以有效提高泛化预测精度。如果模型过于复杂，变量值稍微有点变动，就会引起预测精度问题。正则化之所以有效，就是因为其降低了特征的权重，使得模型更为简单。 正则化一般会采用 L1 范式或者 L2 范式，其形式分别为 [Math] 和 [Math] 。 L1正则化 LASSO 回归，相当于为模型添加了这样一个先验知识： w 服从零均值拉普拉斯分布。 首先看看拉普拉斯分布长什么样子： [公式] 由于引入了先验知识，所以似然函数这样写： [公式] 取 log 再取负，得到目标函数： [公式] 等价于原始损失函数的后面加上了 L1 正则，...
#Machine Learning
READ

二次型优化问题

Math
2025-01-01
问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [公式] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [公式] 我们的目标就是寻找该函数的极值点的坐标，我们把该目标称为 x^∗ . 其中，表示 A ： [公式] 将 A 与多项式系数对应： [公式] [公...
#math
READ

方向导数与梯度

Math
2025-01-01
1. 基本概念 方向导数：是一个数；反映的是f(x,y)在P0点沿方向v的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 2. 方向导数 反映的是f(x,y)在P0点沿方向v的变化率。 例子如下： 方向导数计算公式 偏导数 二元函数偏导数的几何意义 偏导函数 偏导数与偏导函数的关系： 偏导数是偏导函数在指定点的函数值，因此在求偏导数时，也可先求出偏导函数，然后再将点代入偏导函数，从而求出函数在此点的偏导数。 3. 全微分 4. 梯度 梯度是一个向量；既有大小，也有方向。 几何意义 函...
#math
READ

泊松分布和指数分布

Math
2025-01-01
一、泊松分布 日常生活中，大量事件是有固定频率的。 某医院平均每小时出生3个婴儿 某公司平均每10分钟接到1个电话 某超市平均每天销售4包xx牌奶粉 某网站平均每分钟有2次访问 它们的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？ 有可能一下子出生6个，也有可能一个都不出生。这是我们没法知道的。 泊松分布就是描述某段时间内，事件具体的发生概率。 上面就是泊松分布的公式。等号的左边，P 表示概率，N表示某种函数关系，t 表示时间，n 表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1) = 3) 。等号的右边，参数λ是单位时间（或单位面积）内随机事件的平均发生率。 接下来两个小时，一个婴儿都不出生的概率是0.2...
#math
READ

LTR方法小结

Search&Rec
2025-01-01
Learning to rank 排序学习是推荐、搜索、广告的核心方法。排序结果的好坏很大程度影响用户体验、广告收入等。排序学习可以理解为机器学习中用户排序的方法，这里首先推荐一本微软亚洲研究院刘铁岩老师关于LTR的著作，Learning to Rank for Information Retrieval，书中对排序学习的各种方法做了很好的阐述和总结。我这里是一个超级精简版。 排序学习是一个有监督的机器学习过程，对每一个给定的查询－文档对，抽取特征，通过日志挖掘或者人工标注的方法获得真实数据标注。然后通过排序模型，使得输入能够和实际的数据相似。常用的排序学习分为三种类型：PointWise，PairWise和ListWise。 PointWise 单文档方法的处理对象是单独的一篇文档，将文档...
#搜索推荐
READ

ANN (Approximate Nearest Neighbor)

Search&Rec
2025-01-01
1. 概述 新闻推荐系统从海量新闻中推荐出你感兴趣的新闻，百度从海量的搜索结果中找到最优的结果，短视频推荐出你每天都停不下来的视频流，这些里面都包含ANN方法。当然，在现在的检索系统中，往往是多分支并行触发的效果，虽然DNN 大行其道，但是 ANN 一直不可或缺。 通用理解上，ANN（Approximate Nearest Neighbor）是在向量空间中搜索向量最近邻的优化问题。目前业界常用nmslib、Annoy算法作为实现。在实际的工程应用中，ANN是作为一种向量检索技术应用，用于解决长尾Query召回问题。将一个资讯的ANN 召回系统抽象出来大概是下面的样子。 Ann（approximate nearest neighbor）是指一系列用于解决最近邻查找问题的近似算法。最近邻查找问题...
#搜索推荐
READ

正排索引VS倒排索引

Search&Rec
2025-01-01
一句话总结 正排索引：一个未经处理的数据库中，一般是以文档ID作为索引，以文档内容作为记录。 倒排索引：Inverted index，指的是将单词或记录作为索引，将文档ID作为记录，这样便可以方便地通过单词或记录查找到其所在的文档。 倒排索引创建索引的流程 形成文档列表 首先对原始文档数据进行编号（DocID），形成列表，就是一个文档列表。 创建倒排索引列表 对文档中数据进行分词，得到词条。对词条进行编号，以词条创建索引。保存包含这些词条的文档的编号信息。 搜索的过程 当用户输入任意的词条时，首先对用户输入的数据进行分词，得到用户要搜索的所有词条，然后拿着这些词条去倒排索引列表中进行匹配。找到这些词条就能找到包含这些词条的所有文档的编号。 然后根据这些编号去文档列表中找到文档 正排和倒排 正...
#搜索推荐
READ

搜索流程

Search&Rec
2025-01-01
1.倒排索引召回 1）召回模型有三种： 1.基于行为的召回：根据用户的购买行为推荐相关/相似的商品；（长期行为和实时行为） 2.基于用户偏好的召回：用户画像和多屏互通（移动端到PC端）； 3.基于地域的召回； 4.基于搜索词的召回（倒排索引）； 2）倒排索引 倒排是指由属性值来确定记录的位置。 倒排索引由单词词典和倒排文件组成， 单词词典是由文档集合中出现过的所有单词构成的字符串集合，单词词典内每条索引项记载单词本身的一些信息以及指向“倒排列表”的指针。 倒排文件记录所有单词的倒排列表顺序。 好处是在找含有该词的文件时，不需要扫描所有文件，而只需要在单词词典中找到该词，然后找到该词对应的倒排列表即可。 Lucene倒排步骤： 1.取得关键词； 2.建立倒排索引；lucene将上面三列分别作为...
#搜索推荐
READ
1 ... 11 12 13 14 15 ... 24