1. 模型介绍

Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。

Logistic 回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。

1.1 Logistic 分布

Logistic 分布是一种连续型的概率分布，其分布函数和密度函数分别为：

\[ F(x)=P(X\le x)=\frac{1}{1+e^{-(x-\mu)/\gamma}}\\ f(x)=F^{'}(x)=\frac{e^{-(x-\mu)/\gamma}}{\gamma(1+e^{-(x-\mu)/\gamma})^2} \]

其中， $\mu$ 表示位置参数， $\gamma$ 为形状参数。我们可以看下其图像特征：

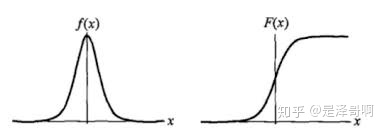
Logistic 分布是由其位置和尺度参数定义的连续分布。Logistic 分布的形状与正态分布的形状相似，但是 Logistic 分布的尾部更长，所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在 $\mu=0,\gamma=1$ 的特殊形式。

1.2 Logistic回归

之前说到 Logistic 回归主要用于分类问题，我们以二分类为例，对于所给数据集假设存在这样的一条直线可以将数据完成线性可分。

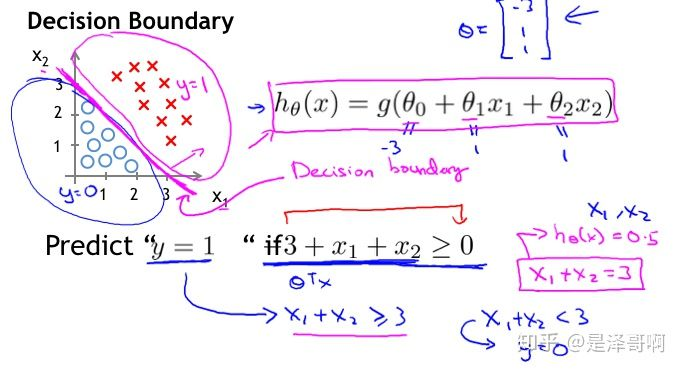
决策边界可以表示为$w_1x_1+w_2x_2+b=0$，假设某个样本点$h_w(x)=w_1x_1+w_2x_2+b>0$那么可以判断它的类别为 1，这个过程其实是感知机。Logistic 回归还需要加一层，它要找到分类概率 $P(Y=1)$ 与输入向量 $x$ 的直接关系，然后通过比较概率值来判断类别。

考虑二分类问题，给定数据集

\[ D=(x_1,y_1),(x_2,y_2),...,(x_N,y_N),x_i\subseteq \mathcal{R}^n,y_i\in0,1,i=1,2,...,N \]

考虑到$w^Tx+b$取值是连续的，因此它不能拟合离散变量。可以考虑用它来拟合条件概率$p(Y=1|x)$，因为概率的取值也是连续的。但是对于$w\ne 0$（若等于零向量则没有什么求解的价值），$w^Tx+b$取值为$\mathcal{R}$，不符合概率取值为 0 到 1，因此考虑采用广义线性模型。

最理想的是单位阶跃函数：

\[ p(y=1|x)=\left\{\begin{aligned} 0 &, & z<0 &\\ 0.5 &, &z=0&, &z=w^Tx+b \\ 1 &, &z>0 \end{aligned}\right. \]

但是这个阶跃函数不可微，对数几率函数是一个常用的替代函数：

\[ y=\frac{1}{1+e^{-(w^Tx+b)}} \]

于是有：

\[ ln\frac{y}{1-y}= w^Tx+b \]

我们将 $y$ 视为 $x$ 为正例的概率，则 $1-y$ 为 $x$ 为其反例的概率。两者的比值称为几率（odds），指该事件发生与不发生的概率比值，若事件发生的概率为 $p$。则对数几率：

\[ ln(odds)=ln\frac{y}{1-y} \]

将 $y$ 视为类后验概率估计，重写公式有：

\[ p(Y=1|x)=\frac{1}{1+e^{-(w^Tx+b)}} \]

也就是说，输出 $Y=1 \(的对数几率是由输入$ x $的**线性函数**表示的模型，这就是**逻辑回归模型**。当$w^Tx+b\)的值越接近正无穷，$p(Y=1|x)$概率值也就越接近 1。因此逻辑回归的思路是，先拟合决策边界(不局限于线性，还可以是多项式)，再建立这个边界与分类的概率联系，从而得到了二分类情况下的概率。

在这我们思考个问题，我们使用对数几率的意义在哪？通过上述推导我们可以看到 Logistic 回归实际上是使用线性回归模型的预测值逼近分类任务真实标记的对数几率，其优点有：

直接对分类的概率建模，无需实现假设数据分布，从而避免了假设分布不准确带来的问题；
不仅可预测出类别，还能得到该预测的概率，这对一些利用概率辅助决策的任务很有用；
对数几率函数是任意阶可导的凸函数，有许多数值优化算法都可以求出最优解。

1.3 代价函数

逻辑回归模型的数学形式确定后，剩下就是如何去求解模型中的参数。在统计学中，常常使用极大似然估计法来求解，即找到一组参数，使得在这组参数下，我们的数据的似然度（概率）最大。

设：

\[ P(Y=1|x)=p(x)\\P(Y=0|x)=1-p(x) \]

似然函数：

\[ L(w)=\prod[p(x_i)]^{y_i}[1-p(x_i)]^{1-y_i} \]

为了更方便求解，我们对等式两边同取对数，写成对数似然函数：

\[ \begin{aligned}L(w)&=\sum [y_ilnp(x_i)+(1-y_i)ln(1-p(x_i)) ]\\&=\sum [y_iln\frac{p(x_i)}{1-p(x_i)}+ln(1-p(x_i))] \\ &=\sum[y_i(w\cdot x_i-ln(1+e^{w\cdot x_i}))]\end{aligned} \]

在机器学习中我们有损失函数的概念，其衡量的是模型预测错误的程度。如果取整个数据集上的平均对数似然损失，我们可以得到:

\[ J(w)=-\frac{1}{N}lnL(w) \]

1.4 求解

求解逻辑回归的方法有非常多，我们这里主要聊下梯度下降和牛顿法。优化的主要目标是找到一个方向，参数朝这个方向移动之后使得损失函数的值能够减小，这个方向往往由一阶偏导或者二阶偏导各种组合求得。逻辑回归的损失函数是：

\[ J(w)=-\frac{1}{n}\sum_{i=1}^{n} [y_ilnp(x_i)+(1-y_i)ln(1-p(x_i)) ] \]

随机梯度下降

梯度下降是通过 $J(w) (对 \(w$ 的一阶导数来找下降方向，并且以迭代的方式来更新参数，更新方式为 ,**上面**\)x_i\)为第$i$个样本，后面用$x^{(i)}$表示，第$i$个样本的第$j$项为$x_j^{(i)}$:

\[ g_j=\frac{\partial J(w)}{\partial w_j}=(p(x^{(i)})-y^{(i)})x_j^{(i)}\\w_j^{k+1}=w_j^k-\alpha g_j \]

其中 $k$ 为迭代次数。每次更新参数后，可以通过比较 $||J(w^{k+1})-J(w^k)||$小于阈值或者到达最大迭代次数来停止迭代。

牛顿法

牛顿法的基本思路是，在现有极小点估计值的附近对$ f(x)$ 做二阶泰勒展开，进而找到极小点的下一个估计值。假设 $w^k$为当前的极小值估计值，那么有：

\[ \varphi(w)=J(w^k)+J^{'}(w^k)(w-w^k)+\frac{1}{2}J^{''}(w^k)(w-w^k)^2 \]

令$\varphi^{'}(w)=0$，得到$w^{k+1}=w^k-\frac{J^{'}(w^k)}{J^{''}(w^k)}$。因此有迭代更新，

\[ w^{k+1}=w^k-\frac{J^{'}(w^k)}{J^{''}(w^k)}=w^k-H_k^{-1}\cdot g_k \]

其中，$H_k^{-1}$是海森矩阵：

\[ H_{mn}=\frac{\partial^2 J(w)}{\partial w_mw_n}=p_w(x^{(i)})(1-p_w(x^{(i)}))x_m^{(i)}x_n^{(i)} \]

此外，这个方法需要目标函数是二阶连续可微的，本文中的 $J(w)$ 是符合要求的。

1.5 正则化

L1正则化与L2正则化

1.6 并行化

从逻辑回归的求解方法中我们可以看到，无论是随机梯度下降还是牛顿法，或者是没有提到的拟牛顿法，都是需要计算梯度的，因此逻辑回归的并行化最主要的就是对目标函数梯度计算的并行化。

我们看到目标函数的梯度向量计算中只需要进行向量间的点乘和相加，可以很容易将每个迭代过程拆分成相互独立的计算步骤，由不同的节点进行独立计算，然后归并计算结果。

下图是一个标签和样本矩阵，行为特征向量，列为特征维度。

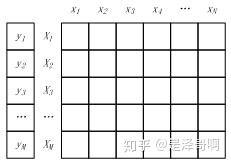
样本矩阵按行划分，将样本特征向量分布到不同的计算节点，由各计算节点完成自己所负责样本的点乘与求和计算，然后将计算结果进行归并，则实现了按行并行的 LR。按行并行的 LR 解决了样本数量的问题，但是实际情况中会存在针对高维特征向量进行逻辑回归的场景，仅仅按行进行并行处理，无法满足这类场景的需求，因此还需要按列将高维的特征向量拆分成若干小的向量进行求解。

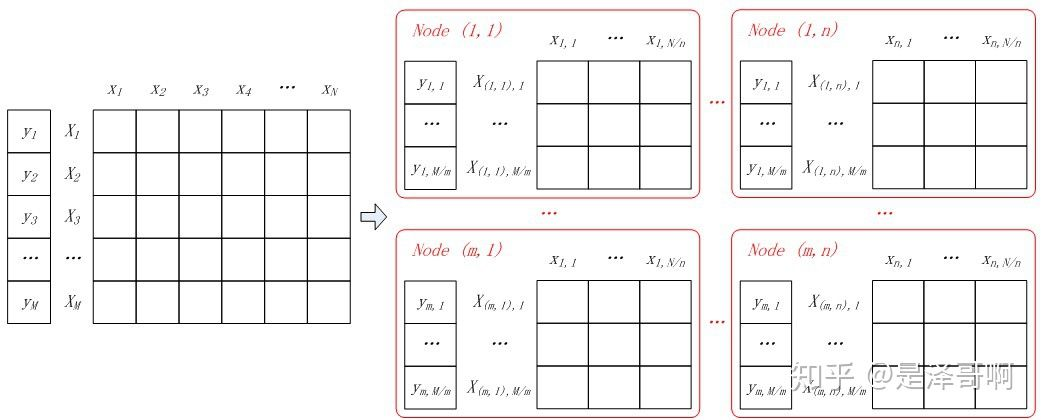
并行计算总共会被分为两个并行化计算步骤和两个结果归并步骤：

步骤一：各节点并行计算点乘，计算$d_{(r,c),k,t}=W_{c,t}^TX_{(r,c),k}$，其中 $k=1,2...,M/m$ ， $d_{(r,c),k,t}$表示第$ t$ 次迭代中节点 $(r,c)$上的第$ k$ 个特征向量与特征权重分量的点乘，$W_{c,t}$为第 $t $次迭代中特征权重向量在第 $c$ 列节点上的分量；
步骤二：对行号相同的节点归并点乘结果：
步骤三：各节点独立算标量与特征向量相乘：
步骤四：对列号相同的节点进行归并：
所以并行计算 LR 的流程如下所示。

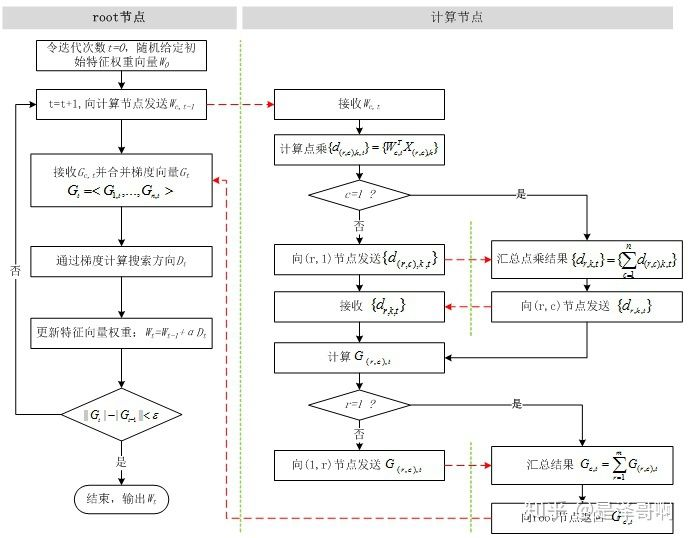
所以并行 LR 实际上就是在求解损失函数最优解的过程中，针对寻找损失函数下降方向中的梯度方向计算作了并行化处理，而在利用梯度确定下降方向的过程中也可以采用并行化。

2. 与其他模型的对比

2.1 与线性回归

逻辑回归是在线性回归的基础上加了一个 Sigmoid 函数（非线形）映射，使得逻辑回归称为了一个优秀的分类算法。本质上来说，两者都属于广义线性模型，但他们两个要解决的问题不一样，逻辑回归解决的是分类问题，输出的是离散值，线性回归解决的是回归问题，输出的连续值。

我们需要明确 Sigmoid 函数到底起了什么作用：

线性回归是在实数域范围内进行预测，而分类范围则需要在 [0,1]，逻辑回归减少了预测范围；
线性回归在实数域上敏感度一致，而逻辑回归在 0 附近敏感，在远离 0 点位置不敏感，这个的好处就是模型更加关注分类边界，可以增加模型的鲁棒性。

2.2 与最大熵模型

逻辑回归和最大熵模型本质上没有区别，最大熵在解决二分类问题时就是逻辑回归，在解决多分类问题时就是多项逻辑回归。

首先进行符号定义：

$\pi(x)_u$表示，输入时 $x$，输出的 $y=u$ 的概率；
$A(u,v)$ 是一个指示函数，若 $u=v$，则 $A(u,v)=1$，否则 $A(u,v)=0$；
我们的目标就是从训练数据中，学习得到一个模型，使得$\pi(x)_u$最大化，也就是输入 $x$，预测结果是 $y \(的概率最大，也就是使得$\pi(x)_u\)最大。

对于逻辑回归而言：

\[ P(Y=1|x)=\pi(x)_1=\frac{e^{w\cdot x}}{1+e^{w\cdot x}}\\P(Y=0|x)=\pi(x)_0=1-\pi(x)_1 \]

这里可以用更泛化的形式来表示 $\pi()$：

\[ \pi(x)_u=\frac{e^{w_v\cdot x}}{\sum_{u=1}^ke^{w_v\cdot x}} \]

回到我们的目标：令$\pi(x_i)_{y_i}$最大，可以用极大似然估计的方法来求解。

\[ L(w)=\prod_{i=1}^n\pi(x_i)_{y_i}\\lnL(w)=\sum_{i=1}^nln(\pi(x_i)_{y_i}) \]

求偏导，得

\[ \frac{\partial}{\partial w_{u,j}}lnL(w)=...=\sum_{i=1,y_i=u}^nx_{ij}-\sum_{i=1}^nx_{ij}\pi(x_i)_u \]