引言与背景

策略梯度方法是强化学习中的一种重要方法，它标志着从基于价值的方法向基于策略的方法的重要转变。之前我们主要讨论了基于价值的方法（value-based），而策略梯度方法则直接优化策略函数(policy-based)，这是一个重要的进步。

当策略用函数表示时，策略梯度方法的核心思想是通过优化某些标量指标来获得最优策略。与传统的表格表示策略不同，策略梯度方法使用参数化函数 $\pi(a|s, \theta)$ 来表示策略，其中 $\theta \in \mathbb{R}^m$ 是参数向量。这种表示方法也可以写成其他形式，如 $\pi_\theta(a|s)$、$\pi_\theta(a, s)$ 或 $\pi(a, s, \theta)$。

策略梯度方法具有多种优势：

更高效地处理大型状态/动作空间
具有更强的泛化能力
样本使用效率更高

策略表示：从表格到函数

当策略的表示从表格转变为函数时，存在以下几个关键区别：

最优策略的定义：
策略更新方式：
获取动作概率：
下面两张图展示了表格和函数表示策略的区别

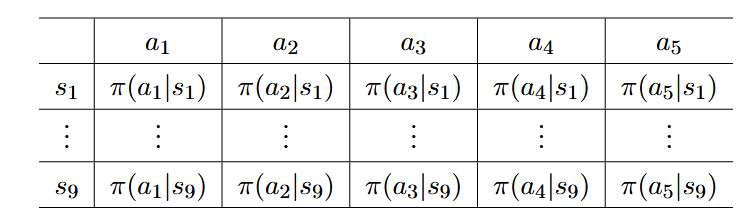
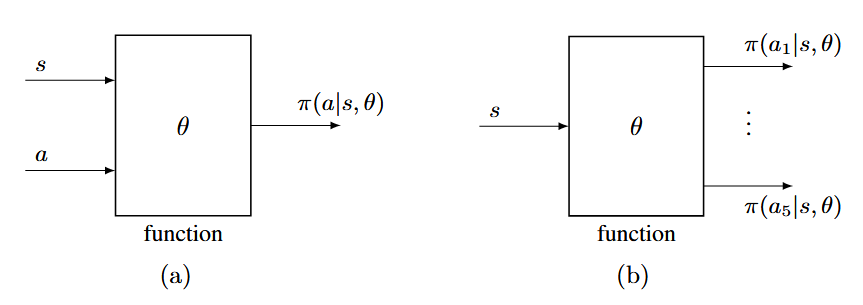
策略函数可以有不同的结构形式（如上图所示）：

输入状态和动作 $(s,a)$，输出选择该动作的概率 $\pi(a|s, \theta)$
输入状态 $s$，输出所有动作的概率分布 $[\pi(a_1|s, \theta), \pi(a_2|s, \theta), ..., \pi(a_n|s, \theta)]$
策略梯度法的基本思想总结如下。假设$ J(\theta)$ 是一个标量度量。可以通过基于梯度的算法优化此指标来获得最佳策略：

\[ \theta_{t+1} = \theta_t+\alpha\nabla_\theta J(\theta_t) \]

定义最优策略的指标

策略梯度方法使用两类主要指标来定义最优策略

平均状态值

平均状态值定义为：

\[ \bar{v}_\pi = \sum_{s \in S} d(s)v_\pi(s) = \mathbb{E}_{S \sim d}[v_\pi(S)] \]

其中 $d(s)$ 是状态 $s$ 的权重，满足 $d(s) \geq 0$ 且 $\sum_{s \in S} d(s) = 1$，因此可以将 $d(s)$ 解释为状态 $s$ 的概率分布。

状态分布 $d$ 的选择有两种情况：

独立于策略 $\pi$ 的分布：
依赖于策略 $\pi$ 的分布：
我们的最终目标是找到一个最优策略（或等效的最优 $θ$）来最大化 $\bar{v}_\pi$。

平均状态值有两个重要的等价表达式：

收集奖励的期望：
向量内积形式：

平均奖励

第二个指标称为 average one-step reward 或者简单称为平均奖励（average reward），定义为：

\[ \begin{equation}\begin{aligned}\bar{r}_\pi &= \sum_{s \in S} d_\pi(s) r_\pi(s) \\&= \mathbb{E}_{S \sim d\pi}[r_\pi(S)]\end{aligned}\end{equation} \]

其中 $d_\pi(s) $ 是稳定态分布，

\[ \begin{equation}r_\pi(s) = \sum_{a \in A} \pi(a|s, \theta)r(s, a) = \mathbb{E}_{A \sim \pi(s,\theta)}[r(s, A)|s]\end{equation} \]

是即时奖励的期望, $r\left( {s,a}\right) \doteq \mathbb{E}\left\lbrack {R | s,a}\right\rbrack = \mathop{\sum }\limits_{r}{rp}(r|s,a)$

平均奖励也有两个等价表达式：

单步奖励的长期平均：假设agent根据策略 $\pi(\theta)$ 收集了奖励 $\{R_{t+1}\}_{t=0}^\infty$，一种在论文中很常见的指标是：
向量内积形式：

两个指标之间的关系

指标的等价性

在折扣情况下（$\gamma < 1$），两个主要指标 $\bar{v}_\pi$ 和 $\bar{r}_\pi$ 是等价的，它们之间存在以下关系：

\[ \bar{r}_\pi = (1 - \gamma)\bar{v}_\pi \]

这个等式表明这两个指标可以同时最大化。也就是说，最大化平均状态值 $\bar{v}_\pi$ 的策略也会最大化平均奖励 $\bar{r}_\pi$，反之亦然。这个等式的证明在后面的引理给出。

指标的不同表达式

下表总结了 $\bar{v}_\pi$ 和 $\bar{r}_\pi$ 这两个指标的不同但等价的表达式：

这些不同的表达式提供了对这些指标的不同理解视角：

表达式1展示了指标作为状态值或即时奖励的加权平均
表达式2将指标表示为期望形式
表达式3将指标与长期累积奖励联系起来
这里还有几点值得说明的是：
我们有时使用 $\bar{v}_\pi$ 特指状态分布为稳态分布 $d\pi$ 的情况，而使用 $\bar{v}_\pi^0$ 指代状态分布 $d_0$ 独立于策略 $\pi$ 的情况。这种区分在推导梯度时很重要，因为不同的状态分布会导致不同的梯度表达式。
所有这些指标都是策略 $\pi$ 的函数。由于策略 $\pi$ 由参数 $\theta$ 参数化，因此这些指标都是 $\theta$ 的函数。换句话说，不同的 $\theta$ 值会生成不同的指标值。因此，我们可以搜索最优的 $\theta$ 值来最大化这些指标。这就是策略梯度方法的基本思想。
策略梯度方法的核心是将策略性能指标表示为参数 $\theta$ 的函数，然后通过优化 $\theta$ 来最大化这些指标。这些指标虽然表达形式不同，但在本质上是等价的，都衡量了策略的长期性能。

策略梯度定理

策略梯度定理是本文最重要的理论结果，它给出了目标函数 $J(\theta)$ 的梯度：

策略梯度定理：$J(\theta)$ 的梯度为

关于策略梯度定理的几点重要说明：

该定理是一个总结所有情况（定理1，2，3）的统一的结论，包含处理不同指标和折扣/非折扣情况的不同场景。
为什么 (8)式可以转换成 (9)式，证明如下：根据期望的定义，(8)式可以重写为：
策略 $\pi(a|s,\theta)$ 必须对所有 $(s,a)$ 为正，以确保 $\ln \pi(a|s,\theta)$ 有效。这可以通过使用 softmax 函数实现：
由于 $\pi(a|s,\theta) > 0$，策略是随机的，因此具有探索性。策略不直接告诉采取哪个动作，而是根据策略的概率分布生成动作。
🧾 ****

蒙特卡罗策略梯度（REINFORCE）

有了策略梯度定理，我们可以使用梯度上升算法来最大化目标函数 $J(\theta)$：

\[ \begin{equation}\begin{aligned}\theta_{t+1} &= \theta_t + \alpha \nabla_\theta J(\theta_t) \\&= \theta_t + \alpha \mathbb{E}[\nabla_\theta \ln \pi(A|S, \theta_t) q_\pi(S, A)]\end{aligned}\end{equation} \]

其中 $\alpha > 0$ 是学习率。

由于真实梯度未知，我们可以用随机梯度替代：

\[ \begin{equation}\theta_{t+1} = \theta_t + \alpha \nabla_\theta \ln \pi(a_t|s_t, \theta_t) q_t(s_t, a_t)\end{equation} \]

其中 $q_t(s_t, a_t)$ 是 $q_\pi(s_t, a_t)$ 的近似值。如果 $q_t(s_t, a_t)$ 通过蒙特卡罗估计获得，该算法称为REINFORCE或蒙特卡罗策略梯度。

这个算法非常重要，因为许多其他策略梯度算法都可以通过扩展它来获得。接下来，我们更仔细地解释这个算法。

由于 $\nabla_\theta \ln \pi(a_t|s_t, \theta_t) = \frac{\nabla_\theta \pi(a_t|s_t,\theta_t)}{\pi(a_t|s_t,\theta_t)}$，我们可以将(13)式重写为：

\[ \theta_{t+1} = \theta_t + \alpha \frac{q_t(s_t, a_t)}{\pi(a_t|s_t, \theta_t)} \nabla_\theta \pi(a_t|s_t, \theta_t) \]

令 $\beta_t = \frac{q_t(s_t, a_t)}{\pi(a_t|s_t, \theta_t)}$，上式可以简洁地写为：

\[ \begin{equation}\theta_{t+1} = \theta_t + \alpha \beta_t \nabla_\theta \pi(a_t|s_t, \theta_t)\end{equation} \]

从这个重写的形式中，可以得出两个重要解释：

策略概率的调整
探索与利用的平衡

采样问题

由于(13)使用样本来近似(12)中的真实梯度，理解样本应该如何获取非常重要：

状态S的采样
动作A的采样
然而，在实践中，由于样本使用效率低，这些理想的采样方式通常不被严格遵循。算法9.1提供了一种更高效的实现方式，先生成一个完整episode，然后使用episode中的每个样本多次更新 $\theta$。

Reference

🔖 https://github.com/MathFoundationRL/Book-Mathematical-Foundation-of-Reinforcement-Learning/blob/main/3%20-%20Chapter%209%20Policy%20Gradient%20Methods.pdf