回顾

PPO

\[ \begin{equation}\begin{aligned}\mathcal{J}_{\text{PPO}}(\theta) &= \mathbb{E}_{(q,a)\sim\mathcal{D}, o_{<t}\sim\pi_{\theta_{\text{old}}}(\cdot|q)} \\ &\left[ \min \left( \frac{\pi_\theta(o_t \mid q, o_{<t})}{\pi_{\theta_{\text{old}}}(o_t \mid q, o_{<t})} \hat{A}_t, \text{clip}\left(\frac{\pi_\theta(o_t \mid q, o_{<t})}{\pi_{\theta_{\text{old}}}(o_t \mid q, o_{<t})}, 1-\varepsilon, 1+\varepsilon\right) \hat{A}_t \right) \right]\end{aligned}\end{equation} \]

其中 $(q, a)$ 是数据集 $\mathcal{D}$ 中采样的 question-answer pair, $\varepsilon$ 是重要性采样比的clip范围, $\hat{A}_t$ 是时间步 $t$ 的优势估计量. 给定 value function $V$ 和 reward function $R$, $\hat{A}_t$ 使用广义优势估计 (GAE) 来计算:

\[ \begin{equation}\begin{aligned}\hat{A}_t^{\text{GAE}(\gamma,\lambda)} = \sum_{l=0}^{\infty} (\gamma\lambda)^l \delta_{t+l}\end{aligned}\end{equation} \]

其中，

\[ \begin{equation}\delta_t = R_t + \gamma V(s_{t+1}) - V(s_t), \quad 0 \leq \gamma, \lambda \leq 1.\end{equation} \]

GRPO

相比于 PPO, GRPO 去掉了value function 并以分组的方式估计优势。对于特定的问答对 (q, a), behavior policy $\pi_{\theta_{\text{old}}}$ 生成了一组 $G$ 个 response $\{o_i\}_{i=1}^G$. 第 $i$ 个 response 的优势是通过对每组奖励 $\{R_i\}_{i=1}^G$ 进行归一化来计算的:

\[ \begin{equation}\hat{A}_{i,t} = \frac{r_i - \text{mean}(\{R_i\}_{i=1}^{G})}{\text{std}(\{R_i\}_{i=1}^{G})}\end{equation} \]

\[ \begin{equation}\begin{aligned}&\mathcal{J}_{\text{GRPO}}(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D}, \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot|q)}\\ &\left[ \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left( \min\left(r_{i,t}(\theta)\hat{A}_{i,t}, \text{clip}\left(r_{i,t}(\theta), 1-\varepsilon, 1+\varepsilon\right)\hat{A}_{i,t}\right) - \beta D_{\text{KL}}(\pi_{\theta}||\pi_{\text{ref}})\right) \right] \end{aligned}\end{equation} \]

其中，

\[ \begin{equation}r_{i,t}(\theta) = \frac{\pi_{\theta}(o_{i,t} \mid q, o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t} \mid q, o_{i,<t})}\end{equation} \]

DAPO(Dynamic sAmpling Policy Optimization)

摘要

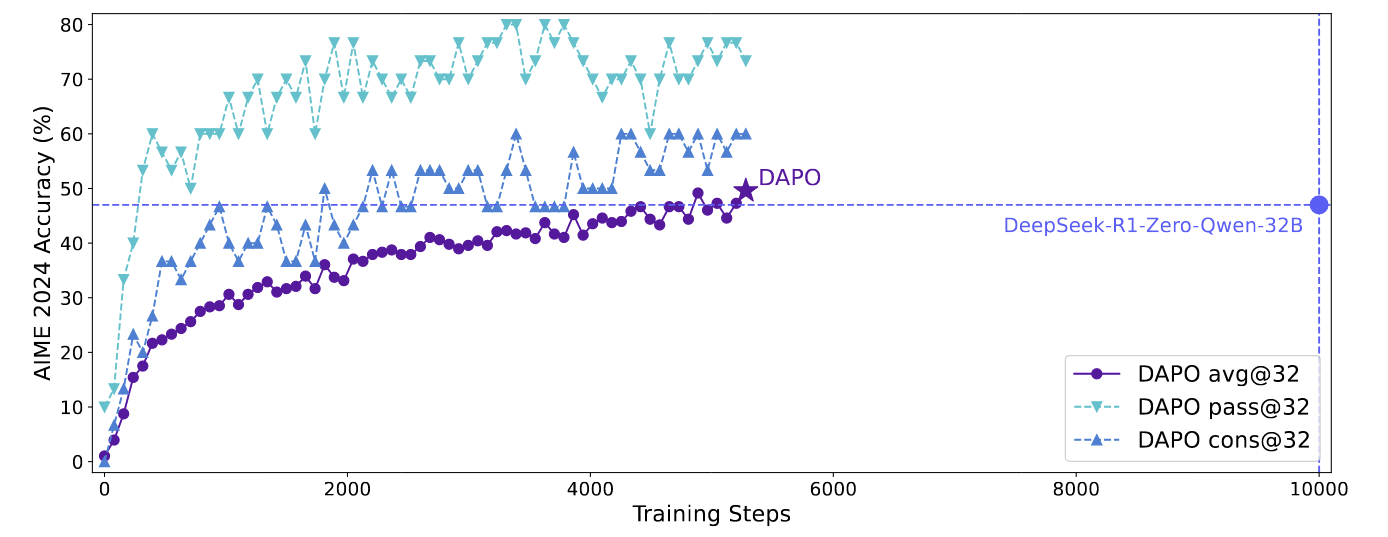
朴素的 GRPO 基线存在几个关键问题，如熵崩塌、奖励噪声和训练不稳定性。在复现 DeepSeek 的结果时遇到了类似的挑战，这表明 R1 论文中可能省略了开发行业级、大规模且可复现的 RL 系统所需的关键训练细节。

为弥补这一差距，提出了解耦裁剪和动态采样策略优化（DAPO）算法，并介绍了 4 个关键技术，使 RL 在长思维链 RL 场景中脱颖而出。

裁剪偏移（Clip-Shifting），促进系统多样性并允许自适应采样；
动态采样（Dynamic Sampling），提高训练效率和稳定性；
Token级策略梯度损失（Token-Level Policy Gradient Loss），在长思维链 RL 场景中至关重要；
溢出奖励塑造（Overflowing Reward Shaping），减少奖励噪声并稳定训练。
DAPO现在已经基于 Verl 做了实现 https://github.com/volcengine/verl

DAPO

提出解耦裁剪和动态采样策略优化（Decouple Clip and Dynamic sAmpling Policy Optimization，DAPO）算法。DAPO 为每个问题 $q$ 及其配对答案 $a$ 采样一组输出 ${o_i}_{i=1}^{G}$，并通过以下目标函数优化策略：

\[ \begin{equation}\begin{aligned}\mathcal{J}_{\text{DAPO}}(\theta) &= \mathbb{E}_{(q,a)\sim\mathcal{D}, \{o_i\}_{i=1}^G \sim \pi{\theta_{\text{old}}}(\cdot|q)}\\& \left[ \color{red}\frac{1}{\sum_{i=1}^{G} |o_i|} \color{black}\sum_{i=1}^{G} \sum_{t=1}^{|o_i|} \min\left(r_{i,t}(\theta)\hat{A}_{i,t}, \text{clip}\left(r_{i,t}(\theta), 1-\color{red}\varepsilon_{\text{low}}\color{black}, 1+\color{red}\varepsilon_{\text{high}}\color{black}\right)\hat{A}_{i,t}\right) \right]\\ \text{where}&\\ &\color{red}\text{s.t.} \quad 0 < \left|\{o_i \mid \text{is\_equivalent}(a, o_i)\}\right| < G \end{aligned}\end{equation} \]

\[ \begin{equation}r_{i,t}(\theta) = \frac{\pi_{\theta}(o_{i,t} \mid q, o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t} \mid q, o_{i,<t})}, \quad \hat{A}_{i,t} = \frac{R_i - \text{mean}(\{R_i\}_{i=1}^{G})}{\text{std}(\{R_i\}_{i=1}^{G})}\end{equation} \]

接下来将介绍与 DAPO 相关的关键技术。

移除 KL 散度

KL 惩罚项用于调节在线策略与冻结参考策略之间的散度。在 RLHF 场景中，RL 的目标是在不偏离初始模型太远的情况下调整模型行为。然而，在训练长思维链推理模型时，模型分布可能与初始模型显著偏离，因此这种限制不是必要的。因此，移除了 KL 项。

Clip-Higher

作者发现，在实际使用 PPO / GRPO 时会出现熵坍塌（entropy collapse）的现象：训练过程中 policy 输出分布的熵快速下降，即对于一个问题，采样出的一个 group 内的回答趋近于相同。这导致 policy 过于确定，exploitation 有余而 exploration 不足，大大限制了强化学习的潜力。

作者认为，这种熵坍塌现象的出现，是由于 PPO-CLIP 中的 upper clip，按照比率 $r=\frac{\pi_\theta}{\pi_{\theta_\text{old}}}$ 限制更新的上限，相当于是打压了低概率 token（exploration token），而鼓励了高概率 token（exploitation token）。

举个例子，PPO-clip 的超参数 $\epsilon$ 的典型值为 0.2，我们考虑优势 $\hat{A}_t>0$的情况，也就是当前动作需要被鼓励（增大该动作被 $\pi_\theta$ 采样出来的概率）的情况。假设有两个动作被 $\pi_{\theta_\text{old}}$采样出来的概率分别是 0.01 和 0.9，那么，由于 clip 操作的限制，我们最大只能把 $\pi_\theta$ 采样出这两个动作的概率分别提升（+20%）到 0.012 和 1.08 。可以看到，由于 clip 限制的是提升的比率，所以原来概率比较低的动作（这些动作可以看作是在做 exploration，所以称为 exploration token）提升的幅度要远远小于概率比较高的动作（这些动作是要最大化累积回报，所以称为 exploitation token），所以说，exploration 被打压了，而 exploitation 更被鼓励。

作者的解决方案是 clip higher，就是把 PPO 中的 lower/upper 两个 clip 超参的设置解耦开，对 upper clip 设置一个比较高的值 $\epsilon_\text{high}$ ，从而让好的动作有更大的提升空间。而 lower clip 的超参 $\epsilon_\text{low}$ 还是要保持相对较小的值，因为如果这个值大了，会对 $\hat{A}_t<0
$ 动作的打压力度更强，导致这些动作更加不可能被采样到，这样也会使得 explore 空间受限。

💡 个人感觉这个 clip higher 不是很对症啊。照文中分析的这个问题，问题的根源在于重要性采样的这个比率 rrr 是按照比例来约束更新上界的，但是 exploration tokens 本身肯定就比 exploitation tokens 概率要低，因此相对提升空间会更小。那么解决方案应该是要重点扶持一下 low prob positive tokens (exploration tokens)。而像 clip higher 这样直接统一拉高 upper epsilon，high prob tokens (exploitation tokens) 不是反而受益会更大吗？

Dynamic Sampling

DAPO 中，延用了 GRPO 的做法：不使用 critic model 来计算 GAE，而是通过基于组内全部采样结果 $\{o_i\}_{i=1}^G$ 的均值和标准差来进行归一化，作为 baseline，计算优势函数 $\hat{A}_t$。这样在极端情况下，即整组的结果全对或全错时，$\hat{A}_t$ 就为零了，也就没有梯度了。这样显然会影响训练效率，尤其是当训练后期，模型能力变强了，组内采样结果全对的情况会更多，对训练效率的影响更大。而且这样梯度的方差也会很大，对模型训练也是不利的。

即公式中 $0 < \left|\{o_i \mid \text{is\_equivalent}(a, o_i)\}\right| < G$，这个约束条件要求在采样的 G 个输出中，与正确答案 $a$ 等价的输出数量必须严格大于 0 且严格小于 G。

解决这个问题的方案很简单，就是在采样时进行过滤，将组内全对或全错的样本直接丢掉，保证组内优势 $\hat{A}_t$ 都是非零的。如果 RL 训练框架不是异步的，而且 rollout 过程不是流水线的话，rollout 占用的时间是由长尾的样本决定的，因此这种情况下加这个过滤策略对训练效率的影响也不会太大。

Token-level policy gradient loss

GRPO 中采用的是 sample level 的损失，即对每个样本的所有 token 先计算平均损失，再算多样本的平均损失。这样相当于是长回答和短回答的权重是相同的，作者认为长回答的权重应该更高，否则对于长回答中的高低质量响应模式无法得到足够强度的鼓励和惩罚。

解决方案就是不再对同一条样本内 token 损失单独进行平均，相当于是对所有 token 做 token level 的 loss。这样相当于对长回答中的高低质量的响应模式的鼓励和惩罚权重就更大了。在 Long CoT 的场景中，比较有用。

Overlong reward shaping

DAPO 的第四点改进，是对于超长回答的惩罚设计，包括 overlong filtering 和 soft overlong punishment 两点。

一般情况下，我们会直接对超出最大长度的样本进行惩罚。但是作者认为这会带来一些噪声，因为一些超长的回答，本身推理过程的思路可能是 ok 的，只是因为超出最大长度，就得到一个负的 reward，对这样的高质量但是超长的回答进行惩罚，可能会让模型比较困惑。

初步解决方案是对于超长的响应，不算对也不算错，直接 mask 掉超长样本的 loss，不要这些样本了，即 overlong filtering。实验发现，这样可以稳定训练并提升性能。

\[ \begin{equation}R_{\text{length}}(y) = \begin{cases} 0, & |y| \leq L_{\max} - L_{cache} \\ \frac{(L_{\max} - L_{cache}) - |y|}{L_{cache}}, & L_{\max} - L_{cache} < |y| \leq L_{\max} \\ -1, & L_{\max} < |y| \end{cases}\end{equation} \]

整体的算法流程如下所示，在各项改进都介绍过之后，应该比较清楚了：

GSPO(Group Sequence Policy Optimization)

GSPO 定义了序列级别的重要性比率，并在序列层面执行裁剪、奖励和优化。相较于 GRPO，GSPO 在以下方面展现出突出优势：

强大高效：GSPO 具备显著更高的训练效率，并且能够通过增加计算获得持续的性能提升；
稳定性出色：GSPO 能够保持稳定的训练过程，并且根本地解决了混合专家（Mixture-of-Experts，MoE）模型的 RL 训练稳定性问题；
基础设施友好：由于在序列层面执行优化，GSPO 原则上对精度容忍度更高，具有简化 RL 基础设施的诱人前景。
以上优点促成了最新的 Qwen3 模型（Instruct、Coder、Thinking）的卓越性能。

动机

模型大小、稀疏性（例如，在专家混合模型中）和响应长度的增长需要较大的rollout batch size，以最大限度地提高 RL 期间的硬件利用率。为了提高样本效率，标准做法是将大量rollout 数据划分为多个小批次以进行梯度更新。此过程不可避免地引入了 off-policy，其中响应 $y$ 是从旧策略 $\pi_{\theta_{\text{old}}}$ 中采样的，而不是当前被优化的策略 $π_θ$。这也解释了 PPO 和 GRPO 中 clip 机制的必要性，它可以防止过度“偏离策略”的样本参与梯度估计。

GRPO 中还存在一个更根本的问题：其目标不明确。当在长响应任务上训练大型模型时，这个问题变得尤为严重，导致灾难性的模型崩溃。GRPO 目标的不当性质源于对重要抽样权重的误用。重要性抽样的原理是通过对从行为分布 $π_{beh}$ 中提取的样本进行重新加权来估计目标分布 $π_{tar}$ 下函数 $f$ 的期望值：

\[ \begin{equation}\mathbb{E}_{z \sim \pi_{\text{tar}}}[f(z)] = \mathbb{E}_{z \sim \pi_{\text{beh}}} \left[ \frac{\pi_{\text{tar}}(z)}{\pi_{\text{beh}}(z)} f(z) \right]\end{equation} \]

这里至关重要的是，这依赖于从行为分布 $\pi_{\text{beh}}$ 中对多个样本（$N \gg 1$）进行平均，通过重要性权重 $\frac{\pi_{\text{tar}}(z)}{\pi_{\text{beh}}(z)}$ 来有效地纠正分布不匹配问题。

但是在GRPO中，其在每个token位置 $ t$ 应用重要性采样：

\[ \begin{equation} \frac{\pi_{\theta}(y_{i,t} \mid x, y_{i,<t})}{\pi_{\theta_{\text{old}}}(y_{i,t} \mid x, y_{i,<t})} \end{equation} \]

由于这个权重是基于从每个next-token分布 $\pi_{\theta_{\text{old}}}(\cdot \mid x, y_{i,<t})$ 中采样的单个样本 $y_{i,t}$，它无法执行预期的分布校正作用。这会导致 GRPO 在训练梯度中引入高方差噪声，噪声在长序列上累积，并被裁剪机制（clipping mechanism）加剧

token级重要性权重的失败指向了一个核心原则：优化目标的单位应该与奖励的单位相匹配。由于奖励是授予整个序列的，因此在token-level上应用 off-policy 似乎有问题。所以GSPO的优化就是去放弃token级别的目标函数，探索利用重要性权重，直接在序列级别（sequence level）执行优化。

方法

由于token级重要性权重存在问题，对应序列级重要性权重：

\[ \begin{equation} \frac{\pi_{\theta}(y \mid x)}{\pi_{\theta_{\text{old}}}(y\mid x)} \end{equation} \]

这个权重具有清晰的理论意义：它反映了从 $\pi_{\theta_{\text{old}}}(\cdot \mid x)$ 中采样的响应 $y$ 与 $\pi_{\theta}(\cdot \mid x)$ 之间的偏离程度。

GSPO的优化目标：

\[ \begin{equation}\begin{aligned} \mathcal{J}_{\text{GSPO}}(\theta) &= \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^{G} \sim \pi_{\theta_{\text{old}}}(\cdot \mid x)} \\ &\left[ \frac{1}{G} \sum_{i=1}^{G} \min\left(s_i(\theta)\hat{A}_i, \text{clip}(s_i(\theta), 1-\varepsilon, 1+\varepsilon)\hat{A}_i\right) \right]\end{aligned}\end{equation} \]

其中，$\hat{A}_i$ 计算方式和GRPO一样，见式4。并定义基于序列似然的重要性比$s_i(\theta)$:

\[ \begin{equation}s_i(\theta) = \left(\frac{\pi_{\theta}(y_i \mid x)}{\pi_{\theta_{\text{old}}}(y_i \mid x)}\right)^{\frac{1}{|y_i|}} = \exp\left(\frac{1}{|y_i|}\sum_{t=1}^{|y_i|} \log \frac{\pi_{\theta}(y_{i,t} \mid x, y_{i,<t})}{\pi_{\theta_{\text{old}}}(y_{i,t} \mid x, y_{i,<t})}\right)\end{equation} \]

这里加入了长度归一化以降低方差并统一 $s_i(\theta)$ 的数值范围。

训练效率与性能

使用基于 Qwen3-30B-A3B-Base 微调得到的冷启动模型进行实验，并汇报其训练奖励曲线以及在 AIME'24、LiveCodeBench 和 CodeForces 等基准上的性能曲线。我们对比 GRPO 作为基线。注意 GRPO 必需采用 Routing Replay 训练策略才能正常收敛（我们将在后文讨论），而 GSPO 则无需该策略。

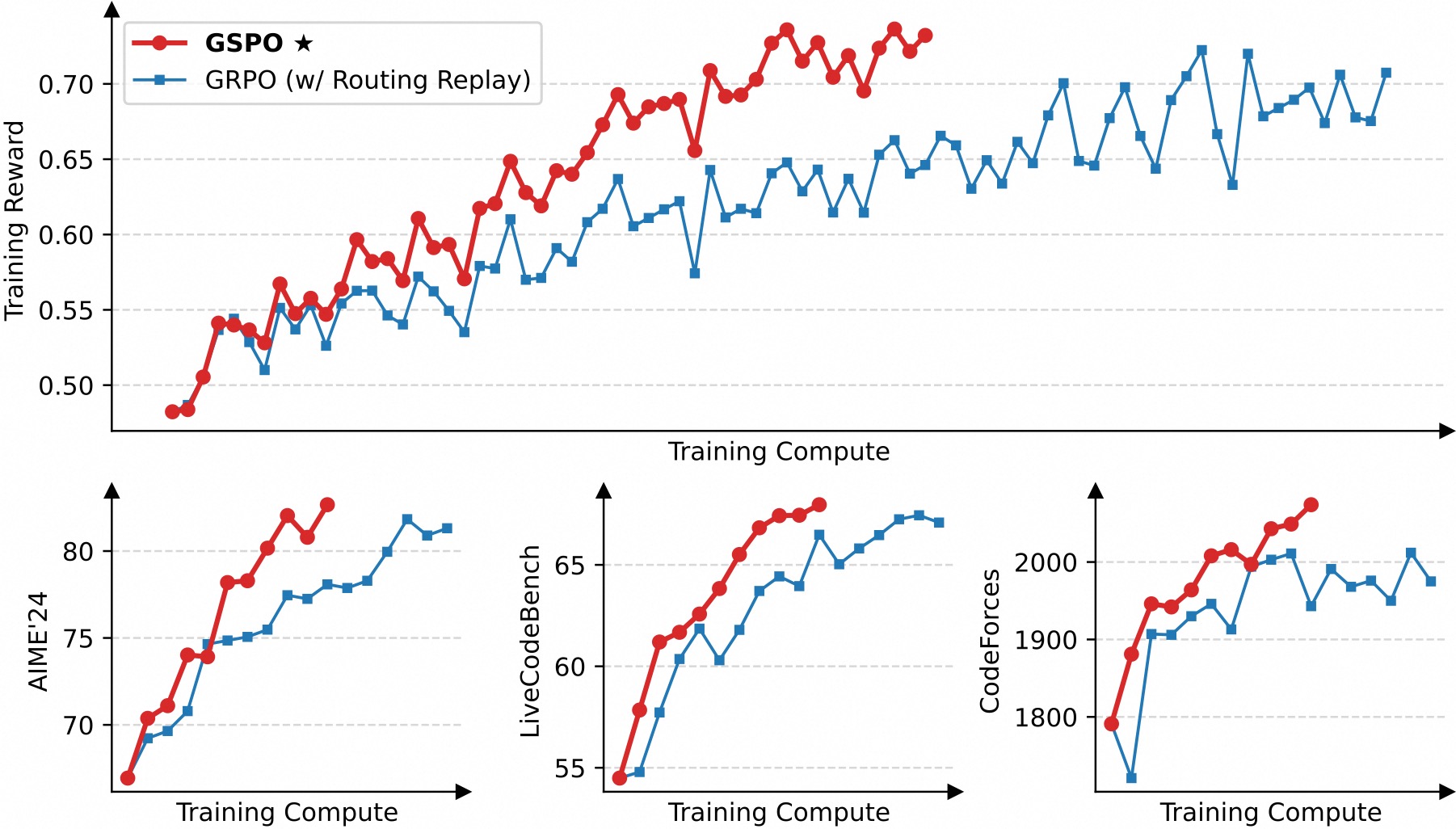
从上图可见，GSPO 表现出比 GRPO 显著更高的训练效率，即在同等计算开销下能够取得更优的性能。特别地，我们观察到 GSPO 可以通过增加算力来获得持续的性能提升——这正是我们所期待的算法的可拓展性。最终，我们成功地将 GSPO 应用于最新的 Qwen3 模型的大规模 RL 训练，进一步释放了 RL scaling 的潜能！

一个有趣的观察是，GSPO 所裁剪的 token 比例比 GRPO 要高上两个数量级（如下图所示），但却具有更高的训练效率。这进一步表明 GRPO 采用的 token 级别的优化目标是有噪和低效的，而 GSPO 的序列级别的优化目标则提供了更可靠、有效的学习信号。

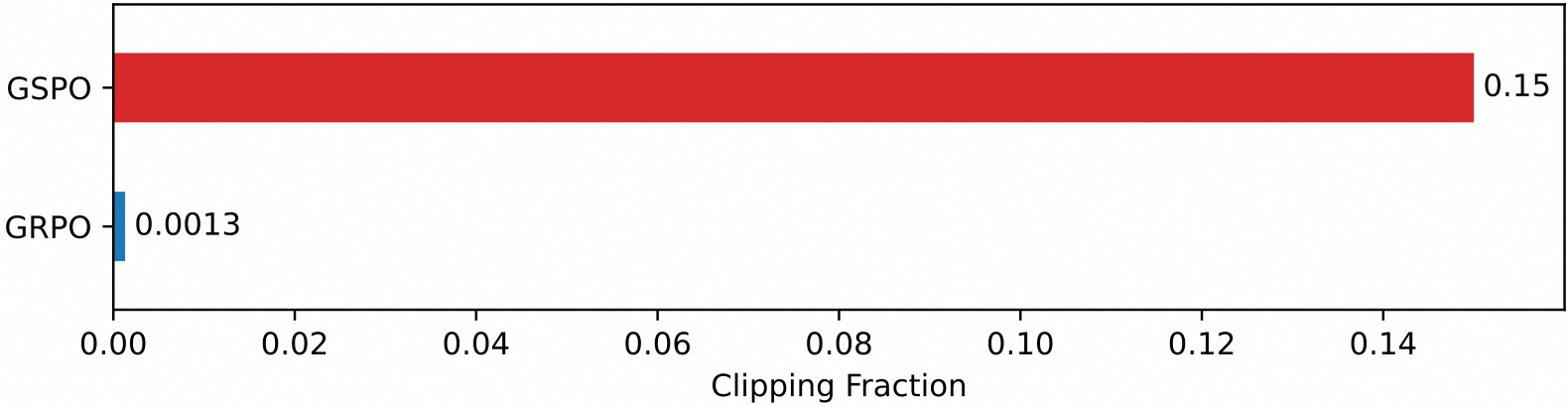
对 MoE RL 和基础设施的收益

我们发现，当采用 GRPO 算法时，MoE 模型的专家激活波动性会使得 RL 训练无法正常收敛。为了解决这一挑战，我们过去采用了 路由回放（Routing Replay）训练策略，即缓存 $\pi_{\theta_{\text{old}}}$ 中激活的专家，并在计算重要性比率时在 $\pi_{\theta}$ 中“回放”这些路由模式。从下图可见，Routing Replay 对于 GRPO 训练 MoE 模型的正常收敛至关重要。然而，Routing Replay 的做法会产生额外的内存和通信开销，并可能限制 MoE 模型的实际可用容量。

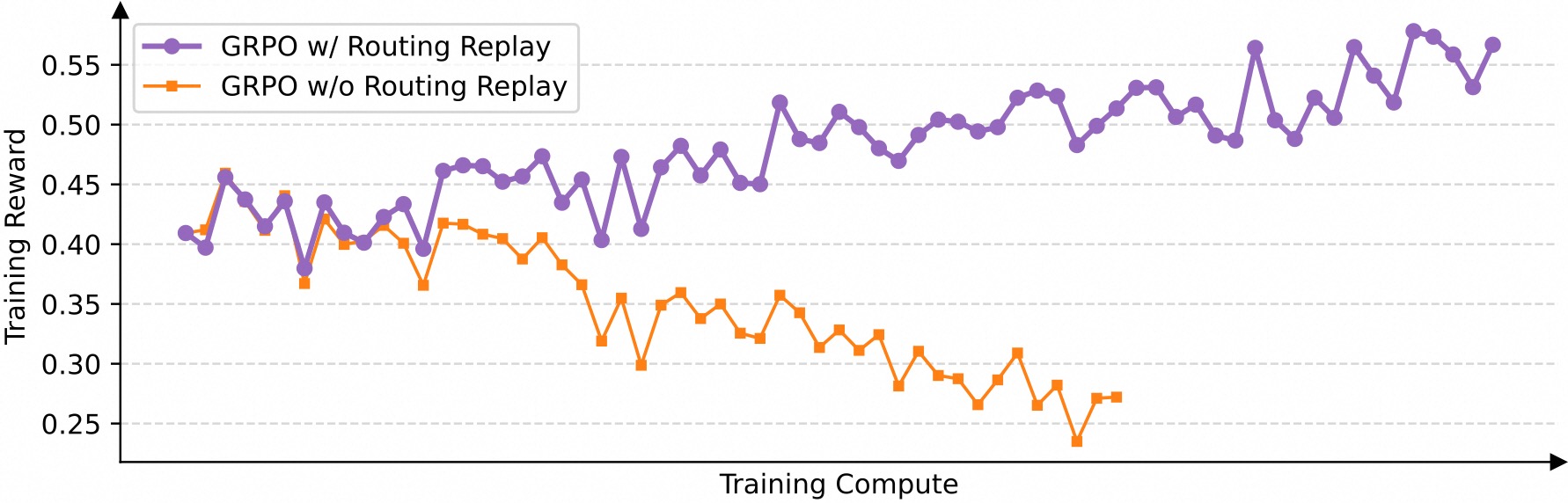
GSPO 的一大突出优势在于彻底消除了对 Routing Replay 的依赖。其核心洞见在于：GSPO 仅关注序列级别的似然（即 $π_θ(y_i∣x)$），而对个别 token 的似然（即 $π_θ(y_i,t∣x,y_{i,<t})$）不敏感。因此，其无需 Routing Replay 等对基础设施负担较大的手段，既简化和稳定了训练过程，又使得模型能够最大化地发挥容量与潜能。

此外，鉴于 GSPO 仅使用序列级别而非 token 级别的似然进行优化，直观上前者对精度差异的容忍度要高得多。因此，GSPO 使得直接使用推理引擎返回的似然进行优化成为可能，从而无需使用训练引擎进行重计算，这在 partial rollout、多轮 RL 以及训推分离框架等场景中特别有益。

💡 ****