💡 GRPO相比PPO主要优势：

背景

GRPO是 DeepSeek-Math model中提出的对PPO方法的改进策略：

强化学习(RL)在提升模型数学推理能力方面被证明是有效的
传统PPO算法需要较大训练资源
GRPO作为PPO的变体被提出,可以更高效地优化模型

PPO回顾

PPO的目标函数为:

\[ \begin{equation}\begin{aligned}J_{PPO}(\theta) = &E_{[q \sim P(Q), o \sim \pi_{\theta_{old}}(O|q)]} \\ &\frac{1}{|o|}\sum_{t=1}^{|o|} min(\frac{\pi_\theta(o_t|q,o_{<t})}{\pi_{\theta_{old}}(o_t|q,o_{<t})}A_t, clip(\frac{\pi_\theta(o_t|q,o_{<t})}{\pi_{\theta_{old}}(o_t|q,o_{<t})}, 1-\epsilon, 1+\epsilon)A_t)\ \ \ \ \ \ \end{aligned}\end{equation} \]

其中:

$\pi_\theta$ 和 $\pi_{\theta_{old}}$ 分别是当前和旧策略模型
$A_t$ 是优势函数
$\epsilon$ 是裁剪相关的超参数

模型训练

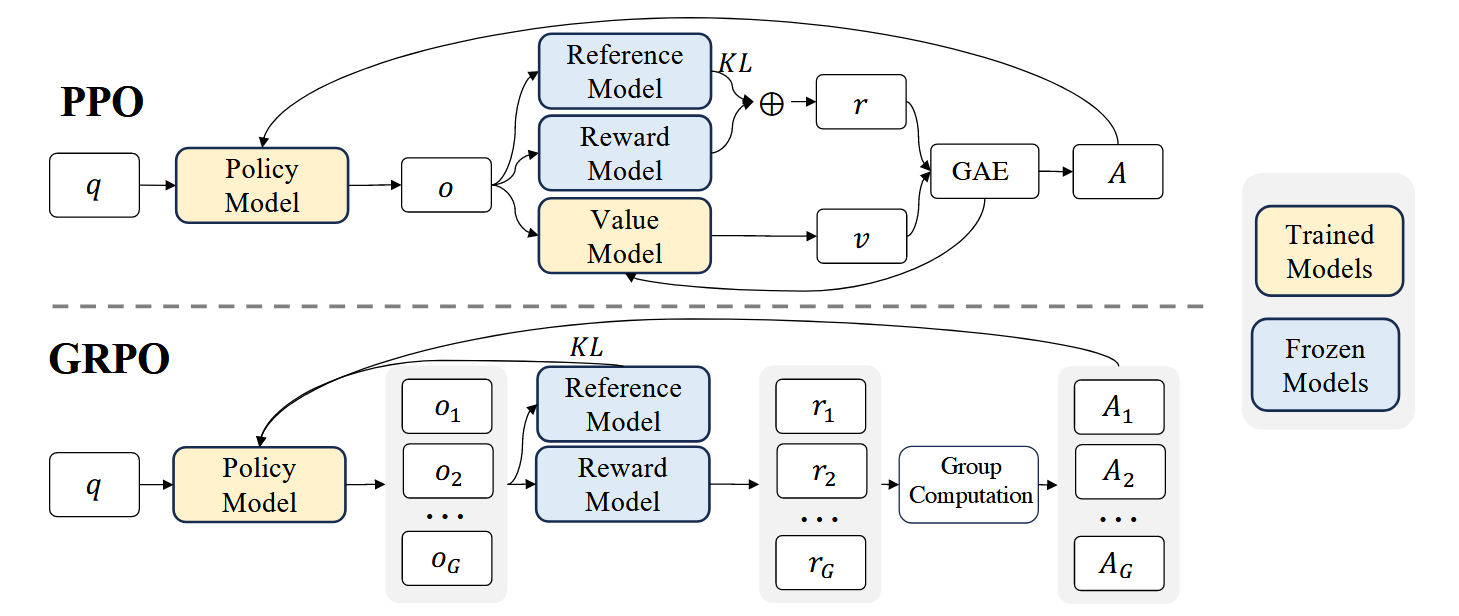
如图1上所示，PPO需要同时训练一个Value Model $V_\psi$ 和策略模型，同时需要reference model（通常从SFT model初始化）来限制策略模型训练保持和reference model的行为接近，而 Reward model用来计算reward：

Value Model 用于基于奖励序列 ${r_{\geq t}}$ 进行优势估计，这增加了额外的计算和内存开销
在每个token位置 $t$，奖励计算公式为：

PPO局限性

计算资源问题：PPO需要训练一个与策略模型相当规模的值函数模型，这带来了巨大的内存和计算负担
值函数训练的困难: 在LLM环境中，奖励模型通常只给最后一个token分配奖励分数, 这使得在每个token位置训练准确的值函数变得复杂，影响了优势估计的准确性

GRPO的具体实现

GRPO核心思想

完全避免使用额外的值函数近似
采用组内相对奖励作为baseline
通过分组采样的方式计算优势
GRPO的目标函数为:

\[ \begin{equation}\begin{aligned} &J_{GRPO}(\theta) = E_{[q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{old}}(O|q)]}\\ &\frac{1}{G}\sum_{i=1}^G\frac{1}{|o_i|}\sum_{t=1}^{|o_i|} min(\frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q,o_{i,<t})}\hat{A}_{i,t}, clip(...)\hat{A}_{i,t}) - \beta \mathbb{D}_{KL}(\pi_\theta||\pi_{ref})\end{aligned}\end{equation} \]

其中：

$\epsilon$ 和 $\beta$ 是超参数
$\hat{A}_{i,t}$ 是基于组内相对奖励计算的优势值
GRPO没有像在 (2)式中一样奖励中添加KL惩罚，而是通过直接添加训练的策略与参考策略之间的KL差异来正则化损失，从而避免使 $\hat{A}_{i,t}$ 的计算复杂化。并且KL散度计算也有一些不同，用了一个无偏估计的KL散度计算：

\[ \begin{equation}{\mathbb{D}}_{KL}\left\lbrack {{\pi }_{\theta }\parallel {\pi }_{\text{ref }}}\right\rbrack = \frac{{\pi }_{\text{ref }}\left( {{o}_{i,t} | q,{o}_{i, < t}}\right) }{{\pi }_{\theta }\left( {{o}_{i,t} | q,{o}_{i, < t}}\right) } - \log \frac{{\pi }_{\text{ref }}\left( {{o}_{i,t} | q,{o}_{i, < t}}\right) }{{\pi }_{\theta }\left( {{o}_{i,t} | q,{o}_{i, < t}}\right) } - 1\end{equation} \]

GRPO的结果监督（Outcome Supervision）

基本流程

采样阶段：对每个问题 q 从旧策略模型 $\pi_{\theta_{old}}$ 采样G个输出: ${o_1, o_2, ..., o_G}$
奖励计算：使用奖励模型对每个输出进行评分得到G个奖励值: $r = {r_1, r_2, ..., r_G}$
奖励归一化：对原始奖励进行标准化处理：
对输出序列中的 $o_i$ 中的所有token t 使用相同的优势值，优势值等于归一化后的奖励值
这样做的好处是：

相对比较：通过组内归一化实现输出间的相对比较，减少了不同问题间奖励尺度的差异
方差减少：标准化处理有助于稳定训练，控制了优势值的分布范围
简化优势分配：统一分配所有token获得相同的优势值，简化了优势估计过程
端到端反馈：基于最终结果对整个序列进行优化，适合于结果导向的任务
这种结果监督机制的设计体现了GRPO算法在实用性和效率之间的权衡，通过简化优势计算来提高训练效率，同时保持了足够的效果。这对于大规模语言模型的强化学习优化特别有价值。
去除了critic模型
使用组内得分作为baseline估计

GRPO的过程监督(Process Supervision)

结果监督只在输出结束时提供奖励，对复杂数学任务的监督可能不够充分，需要对推理过程中的每个步骤进行评估。

基本流程

对问题q采样G个输出：${o_1, o_2, ..., o_G}$
使用过程奖励模型对每个推理步骤进行评分，得到对应的奖励：
计算归一化奖励
基于后续步骤的奖励计算token优势值
这样实现的优势是

更细粒度的监督：
更好的奖励分配：
适合多步推理问题，需要清晰推理过程的任务比如数学问题求解和复杂逻辑的推理

具体示例

这里再对比一下GRPO和PPO在计算优势函数上的差异：

假设我们有一个数学问题：

Q: "计算 13 × 17 的结果"

模型生成了多个答案：

PPO的计算方式

需要训练一个值函数模型 $V_\psi(s_t)$
对每个token位置都要计算值函数预测
使用 $TD(λ)$ 或 $GAE(λ)$ 计算优势值
更新策略
以输出1为例：

Token序列: ["让", "我们", "一步", "步", "计算", "：", "1", ".", " ", "13", "×", "10", "=", "130", ...]
值函数预测: [0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.6, 0.65, 0.7, 0.75, 0.8, ...]

实际奖励: r = 1 (正确答案)

优势值计算(使用GAE):
$A_t = r_t + γV(s_{t+1}) - V(s_t)$

GRPO Outcome Supervision 的计算方式

采样一组输出(G个)
计算组内奖励统计量
归一化奖励
将归一化奖励作为整个序列的优势
更新策略
对同一问题采样G个输出（例如G=3）：

组内采样结果:
输出1: 完整推导过程，答案221 → $ r₁ = 1.0$
输出2: 直接答案220 → $r₂ = 0.0$
输出3: 直接答案221 → $r₃ = 1.0$

GRPO Process Supervision 的计算方式

采样一组输出(G个)
计算组内奖励统计量
归一化奖励
基于后续步骤的奖励计算token优势值（每个步骤的优势值相同）
更新策略
对同一问题采样G个输出（例如G=3）：

组内采样结果:

关键区别对比

迭代式GRPO

随着策略模型的改进，旧的奖励模型可能变得不够competent，奖励模型需要与策略模型同步更新，并且需要保持历史经验的连续性

所以迭代式的GRPO核心思想是：

动态更新奖励模型（使用新生成的数据）
使用replay机制保留历史经验（保留10%的历史数据）
策略模型和奖励模型交替优化