💡 ****

引言

Trust Region Policy Optimization (TRPO) 是2015年的ICML会议上提出的一种强大的基于策略的强化学习算法。TRPO 解决了传统策略梯度方法中的一些关键问题，特别是训练不稳定和步长选择困难的问题。与传统策略梯度算法相比，TRPO 具有更高的稳健性和样本效率，能够在复杂环境中取得更好的性能。

优化基础

在深入了解 TRPO 之前，我们需要先简单回顾一些优化方法的基础知识。

梯度上升法

梯度上升法是一种迭代优化算法，用于寻找函数的局部最大值。

目标：找到使目标函数 \(J(\theta)\) 最大化的参数 \(\theta^*\)：

\[ \theta^* = \arg\max_\theta J(\theta) \]

梯度上升迭代过程：

在当前参数 \(\ \theta_{old}\) 处计算梯度：\(g = \frac{\partial J(\theta)}{\partial \theta}|_{\theta=\theta_{old}}\)
更新参数：
梯度上升法的主要问题是学习率的选择：

学习率太小：收敛速度慢
学习率太大：可能导致发散或在最优点附近震荡

随机梯度上升法

在强化学习中，目标函数通常是期望形式：

\[ J(\theta) = \mathbb{E}_S[V(S;\theta)] \]

随机梯度上升迭代过程：

随机采样状态 \(s\)
在当前参数 \(\theta_{old}\) 处计算梯度：\(g = \frac{\partial V(s;\theta)}{\partial \theta}|_{\theta=\theta_ {old}}\)
更新参数：
随机梯度上升法的优点是计算效率高，但缺点是梯度估计有噪声，可能导致训练不稳定。

信任区域 (Trust Region) 方法

信任区域方法是一类优化算法，它通过限制每次参数更新的步长来提高优化过程的稳定性。这种方法特别适合处理非凸优化问题，而强化学习中的策略优化正是一个典型的非凸优化问题。

信任区域（Trust Region）是当前参数点 \(\theta_{old}\) 的一个邻域 \(\mathcal{N}(\theta_{old})\)，在这个区域内，我们认为目标函数的近似模型是可靠的。

最常见的信任区域定义是欧几里得球：

\[ \mathcal{N}(\theta_{old}) = \{\theta \mid ||\theta - \theta_{old}|| \leq \Delta\} \]

其中 \(\Delta\) 是信任区域半径，控制了每次更新的最大步长, 如下图所示

信任区域算法的核心思想是：在每次迭代中，我们在当前参数点附近构建目标函数的一个近似模型，然后在信任区域内最大化这个近似模型。

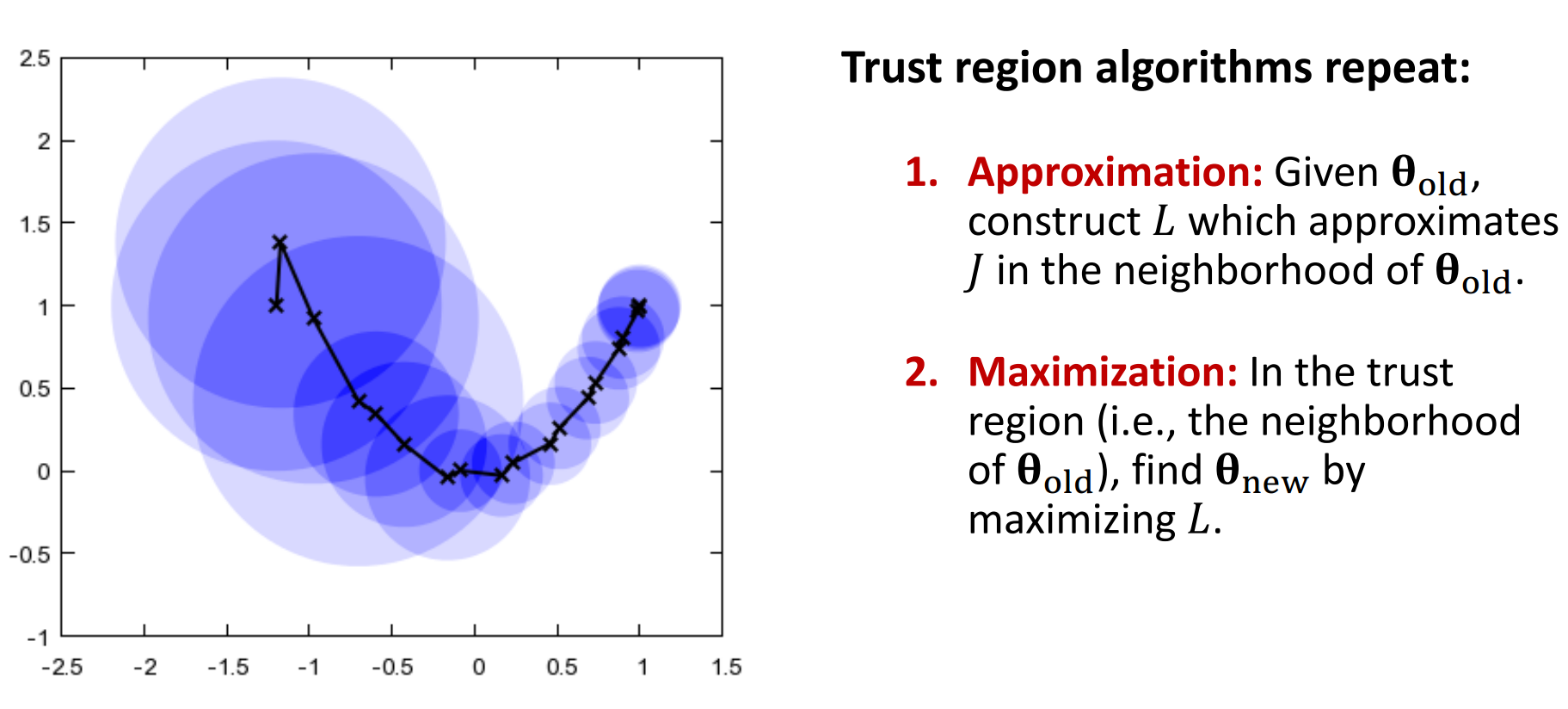
信任区域算法流程：

近似：给定当前参数 \(\theta_{old}\)，构建函数 \(L(\theta|\theta_{old})\) 作为目标函数 \(J(\theta)\) 在 \(\theta_{old}\) 邻域内的近似，如下图中紫线，
最大化：在信任区域内找到参数更新：
最终经过不断的迭代，可以找到一个最优的 \(\theta^*\) 收敛到局部最优值，总体可以用下面这张图来总结：

信任区域方法相比传统梯度方法有几个重要优势：

自适应步长：信任区域半径 \(\Delta\) 可以根据近似模型的准确性动态调整，避免了手动调整学习率的麻烦
更好的稳定性：通过限制每次更新的步长，避免了参数空间中的"悬崖"导致的灾难性更新
处理非凸优化：在非凸优化问题中，梯度方法容易陷入鞍点，而信任区域方法能够更有效地逃离鞍点

基于策略的强化学习

在进入正题之前还需要再简单回顾一下基于策略的强化学习的相关概念，在基于策略的强化学习中，我们直接参数化策略 \(\pi(a|s;\theta)\)，表示在状态 \(s\) 下选择动作 \(a\) 的概率。

状态价值函数：

\[ \begin{equation}V_\pi(s) = \mathbb{E}_{A\sim\pi}[Q_\pi(s,A)] = \sum_{a}\pi(a|s;\theta) \cdot Q_\pi(s,a)\end{equation} \]

其中 \(Q_\pi(s,a)\) 是状态-动作价值函数，表示在状态 \(s\) 下执行动作 \(a\) 并之后遵循策略 \(\pi\) 的期望回报。

目标函数：

\[ J(\theta) = \mathbb{E}_S[V_\pi(S)] \]

这个目标函数表示在初始状态分布下，遵循策略 \(\pi\) 的期望回报。

策略梯度方法

策略梯度方法通过梯度上升来最大化目标函数 \(J(\theta)\)。根据策略梯度定理，目标函数的梯度可以表示为：

\[ \nabla_\theta J(\theta) = \mathbb{E}_{s,a}[\nabla_\theta \ln\pi(a|s;\theta) \cdot Q_\pi(s,a)] \]

这个梯度可以通过采样轨迹来估计，但估计的梯度通常有高方差，导致训练不稳定。

Trust Region Policy Optimization (TRPO)

存在的问题

为理解 TRPO 的必要性，需要先了解传统策略梯度方法（如 REINFORCE 或 Actor-Critic）存在的问题：

优化不稳定
固定学习率的局限性
参数空间与策略空间不一致
样本效率低
与 PG 方法相关的一个缺点是样本效率。对于 PG 方法，我们需要为单个策略参数更新采样整个轨迹。轨迹中可能有数千个时间步，甚至更多，这取决于环境，而为了获得最优策略，我们需要根据训练过程和初始参数值进行多次更新。正如我们所看到的，这相当低效。但为什么我们不在每个时间步进行一次更新呢？这个问题的答案在于处理高维 RL 问题的函数逼近器的需求。众所周知，表格型 RL 方法不适合具有大状态和动作空间的问题。但你有没有想过，为什么只有有限数量的参数能够以相当高的精度逼近无限数量的状态-动作值？这是因为这种连续环境中的状态彼此之间密切相关。为了可视化，想象一下环境是一个大迷宫。通常，智能体当前所在状态的价值与距离它几厘米的状态的价值相差不大。因此，状态是紧密相关的。
所以，上面强调的四个点告诉我们与正常 PG 方法相关的缺点以及需要更好的优化技术。基本上，我们想要确保两件事：

我们需要限制策略的变化，以便新旧策略之间的差异不大。
同时，我们应确保任何策略变化都能保证奖励的单调增加。
TRPO 可以确保这一点！！

目标函数推导

TRPO 的目标是最大化 \(J(\theta)\)，但直接优化这个目标函数很困难。因此，TRPO 构造了一个替代目标函数。

从状态价值函数开始, 我们可以引入旧策略 \(\pi_{old} = \pi(\cdot|\cdot;\theta_{old})\) 并将 (1) 重写为：

\[ V_\pi(s) = \sum_{a}\pi(a|s;\theta_{old}) \cdot \frac{\pi(a|s;\theta)}{\pi(a|s;\theta_{old})} \cdot Q_\pi(s,a) \]

这可以表示为期望形式：

\[ V_\pi(s) = \mathbb{E}_{A\sim\pi_{old}}[\frac{\pi(A|s;\theta)}{\pi(A|s;\theta_{old})} \cdot Q_\pi(s,A)] \]

因此，对应的目标函数可以写为：

\[ J(\theta) = \mathbb{E}_S[V_\pi(S)] = \mathbb{E}_{S,A}[\frac{\pi(A|S;\theta)}{\pi(A|S;\theta_{old})} \cdot Q_\pi(S,A)] \]

这个形式的目标函数使得我们可以使用重要性采样，基于旧策略 \(\pi_{old}\) 收集的数据来评估新策略 \(\pi_\theta\)。

TRPO 算法

近似步骤
最大化步骤

优化问题的解决方案 (Optional)

至于怎么求解并优化这个优化问题的过程可以参考原论文 Trust Region Policy Optimization

TRPO 原论文中使用泰勒多项式近似和共轭梯度算法求解优化问题。

并且和上文的符号有所区分，并且一些细节上也不太一样（比如上文的状态价值函数使用的是\(Q\)，而，论文中用的带baseline版本，也就是优势函数\(A\)），但整体思路相同。

泰勒展开近似：
自然策略梯度：
共轭梯度算法：
最终，可以给出TRPO的算法伪代码如下

PPO（Proximal Policy Optimization）

简介

文章首先指出了当前三种主流强化学习方法的缺点：

深度Q学习（Deep Q-learning）：在许多简单问题上失效并且理论理解不充分
"原始"策略梯度方法（"Vanilla" Policy Gradient）：数据效率低，模型的鲁棒性差
信任区域策略优化（TRPO）：
因此，如果我们因为近似二阶优化问题而引入了误差，就回到我们熟悉的第一阶优化方法，这些方法在计算上更容易处理。此外，有时调整策略参数以避免导致改进也是可以的。也就是说，我们并不需要在每次更新时都保证单调改进。这意味着我们不应该对短期目标过于贪婪，而应该更多地关注实现收敛到全局最优策略的长期目标。

所以openai提出了Proximal Policy Optimization (PPO) ，这是一种新型的策略梯度强化学习算法，它在保持信任区域策略优化(TRPO)的性能和稳定性的同时，提供了更简单的实现方式和更好的采样复杂度。它的简单性和效率使其成为大多数强化学习（RL）应用中的默认算法。

近端策略优化是一种基于策略的算法，通过调整策略参数（由函数近似器如神经网络参数化）来构建随机策略。它可用于具有连续和离散动作空间的无限状态空间环境。

我们可以选择这两种方法中的任何一种来对GRPO进行改进。

构建更复杂的方法来近似这些二阶导数矩阵，以降低计算复杂度。
通过添加一些软约束（以确保新旧策略之间差异不大，并且随着时间的推移进行策略改进，尽管不是严格单调的）来缩小一阶和二阶优化方法之间的差距。
PPO 采用了一种类似于第二种方法的方法。是的，PPO 是一种一阶优化方法！！, PPO 有两种版本。让我们逐一看看它们。

PPO with adavptive KL-Penalty

这种方法与我们在 TRPO 中做的方法类似，除了我们使用随机梯度上升这种一阶优化方法，并根据需求调整 KL 惩罚项，对应的目标公式如下：

\[ \begin{equation}{L}^{KLPEN}\left( \theta \right) = {\hat{\mathbb{E}}}_{t}\left\lbrack {\frac{{\pi }_{\theta }\left( {{a}_{t} \mid {s}_{t}}\right) }{{\pi }_{{\theta }_{\text{old }}}\left( {{a}_{t} \mid {s}_{t}}\right) }{\hat{A}}_{t} - \beta \operatorname{KL}\left\lbrack {{\pi }_{{\theta }_{\text{old }}}\left( {\cdot \mid {s}_{t}}\right) ,{\pi }_{\theta }\left( {\cdot \mid {s}_{t}}\right) }\right\rbrack }\right\rbrack\end{equation} \]