FM：Factorization Machines, 2010 —— 隐向量学习提升模型表达

优势：

可以有效处理稀疏场景下的特征学习
具有线性时间复杂度
对训练集中未出现的交叉特征信息也可进行泛化
不足：
2-way的FM仅枚举了所有特征的二阶交叉信息，没有考虑高阶特征的信息

2-way的FM仅枚举了所有特征的二阶交叉信息，没有考虑高阶特征的信息
FFM（Field-aware Factorization Machine）是Yuchin Juan等人在2015年的比赛中提出的一种对FM改进算法，主要是引入了field概念，即认为每个feature对于不同field的交叉都有不同的特征表达。FFM相比于FM的计算时间复杂度更高，但同时也提高了本身模型的表达能力。FM也可以看成只有一个field的FFM，这里不做过多赘述。AFM：Attentional Factorization Machines, 2017 —— 引入Attention机制的FM

AFM：Attentional Factorization Machines, 2017 —— 引入Attention机制的FM

FM中组合特征的权重不再是独立的。对于一些无用的特征，应该设置很低的权重，但是FM缺少这个作用。本文引入attention机制来解决这个问题。自动学习组合特征的不同的权重。

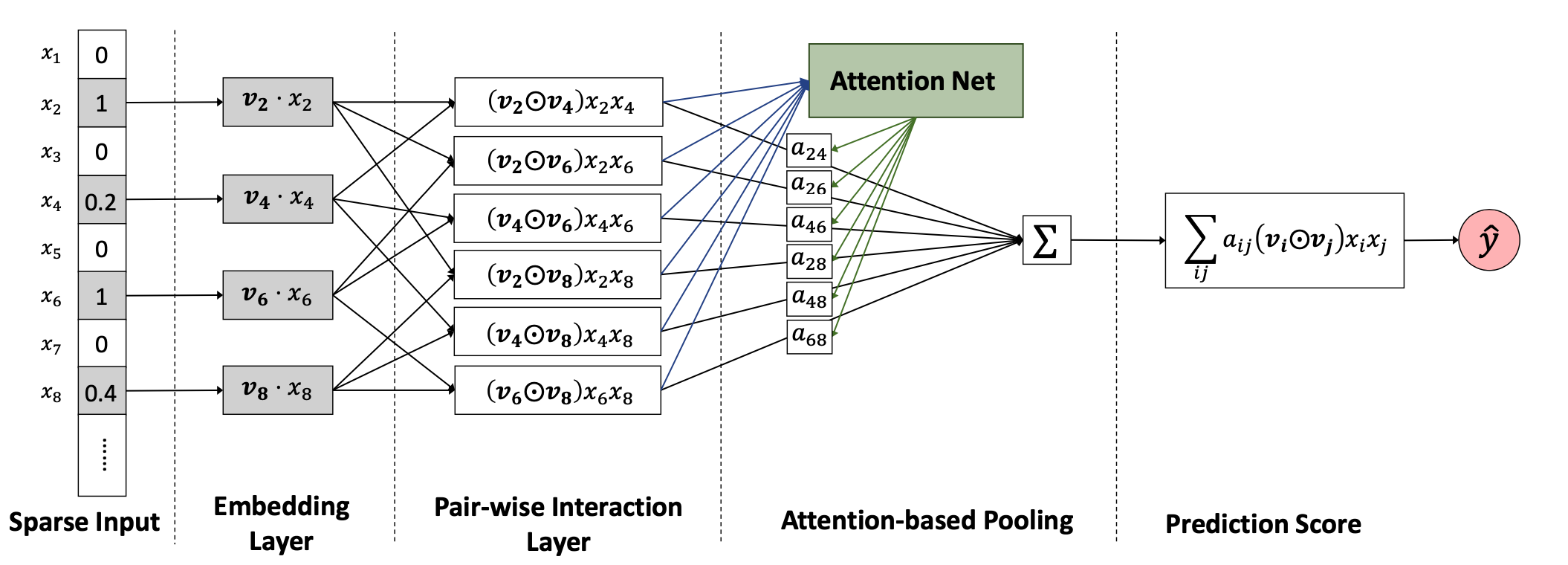
Input layer&Embedding layer

去掉零值的特征 $x\in\mathcal{X}$，经过embedding层后得到，$\varepsilon=\{v_ix_i\}_{i\in \mathcal{X}}$

Pair-wise Interaction Layer

受到FM的启发，使用内积得到组合特征（each pair of features），现在提出Pair-wise Interaction Layer，如果特征向量大小为m，通过这一层后会得到大小为m(m − 1)/2的组合特征向量。把embedding后的向量进行两两组合，得到：

$$
f_{PI}(\varepsilon)={( \mathbf{v}i\odot\mathbf{v}_j)x_ix_j}{(i,j)\in\mathcal{R_x}}

经过一个pooling和全连接层，得到预测值。

$$
\hat{y}=P^T\sum_{(i,j)\in\mathcal{R_x}}( \mathbf{v}_i\odot\mathbf{v}_j)x_ix_j+b

其中$P\in\mathcal{R^k}$为权重，$b\in\mathcal{R}$为偏差，若$P$全为1，即所有特征的权重为1，$b$为0，则此模型变成FM模型。

Attention-based Pooling Layer

$$
f_{Att}(f_{PI}(\varepsilon))=\sum_{(i,j)\in\mathcal{R_x}}a_{ij}( \mathbf{v}_i\odot\mathbf{v}_j)x_ix_j

其中$a_{ij}$是特征交互$\hat{w}_{ij}$的注意力得分，可以解释为$\hat{w}_{ij}$在预测目标中的重要性。

$a_{ij}$的值是通过最小化损失函数得到的，所以还需要加入MLP，将此层称为attention network，现定义为：

\[ a^{'}_{ij}=h^TReLU(\mathbf{W}(\mathbf{v}_i\odot\mathbf{v}_j)x_ix_j+\mathbf{b})\\a_{ij}=\frac{exp(a^{'}_{ij})}{\sum_{(i,j){\in\mathcal{R_x}}}exp(a^{'}_{ij})} \]

优势：

在FM的二阶交叉项上引入Attention机制，赋予不同交叉特征不同的重要度，增加了模型的表达能力
Attention的引入，一定程度上增加了模型的可解释性
不足：
仍然是一种浅层模型，模型没有学习到高阶的交叉特征

Embedding+MLP结构下的浅层改造

FNN： Factorization Machine supported Neural Network, 2016 —— 预训练Embedding的NN模型

FNN是2016年提出的一种基于FM预训练Embedding的NN模型，其思路也比较简单；FM本身具备学习特征Embedding的能力，DNN具备高阶特征交叉的能力，因此将两者结合是很直接的思路。FM预训练的Embedding可以看做是“先验专家知识”，直接将专家知识输入NN来进行学习。注意，FNN本质上也是两阶段的模型，与Facebook在2014年提出GBDT+LR模型在思想上一脉相承。

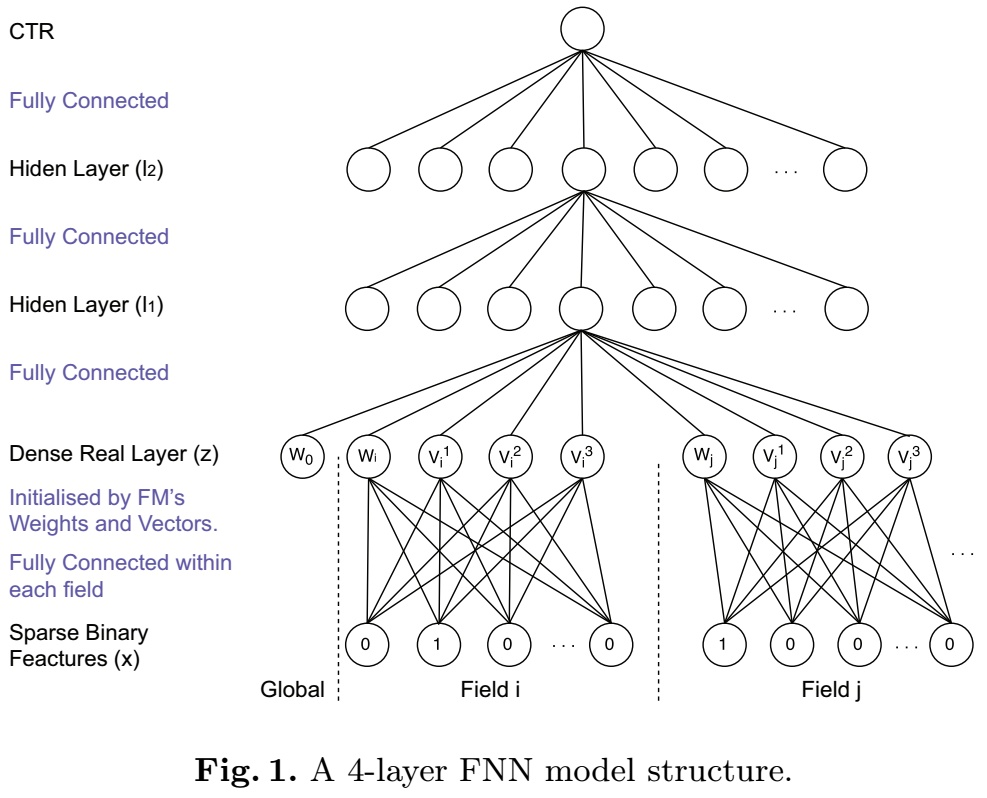
FNN本身在结构上并不复杂，如上图所示，就是将FM预训练好的Embedding向量直接喂给下游的DNN模型，让DNN来进行更高阶交叉信息的学习。

优势：

离线训练FM得到embedding，再输入NN，相当于引入先验专家经验
加速模型的训练和收敛
NN模型省去了学习feature embedding的步骤，训练开销低
不足：
非端到端的两阶段模型，不利于online learning
预训练的Embedding受到FM模型的限制
FNN中只考虑了特征的高阶交叉，并没有保留低阶特征信息

PNN：Product-based Neural Network, 2016 —— 引入不同Product操作的Embedding层

PNN是2016年提出的一种在NN中引入Product Layer的模型，其本质上和FNN类似，都属于Embedding+MLP结构。作者认为，在DNN中特征Embedding通过简单的concat或者add都不足以学习到特征之间复杂的依赖信息，因此PNN通过引入Product Layer来进行更复杂和充分的特征交叉关系的学习。PNN主要包含了IPNN和OPNN两种结构，分别对应特征之间Inner Product的交叉计算和Outer Product的交叉计算方式。

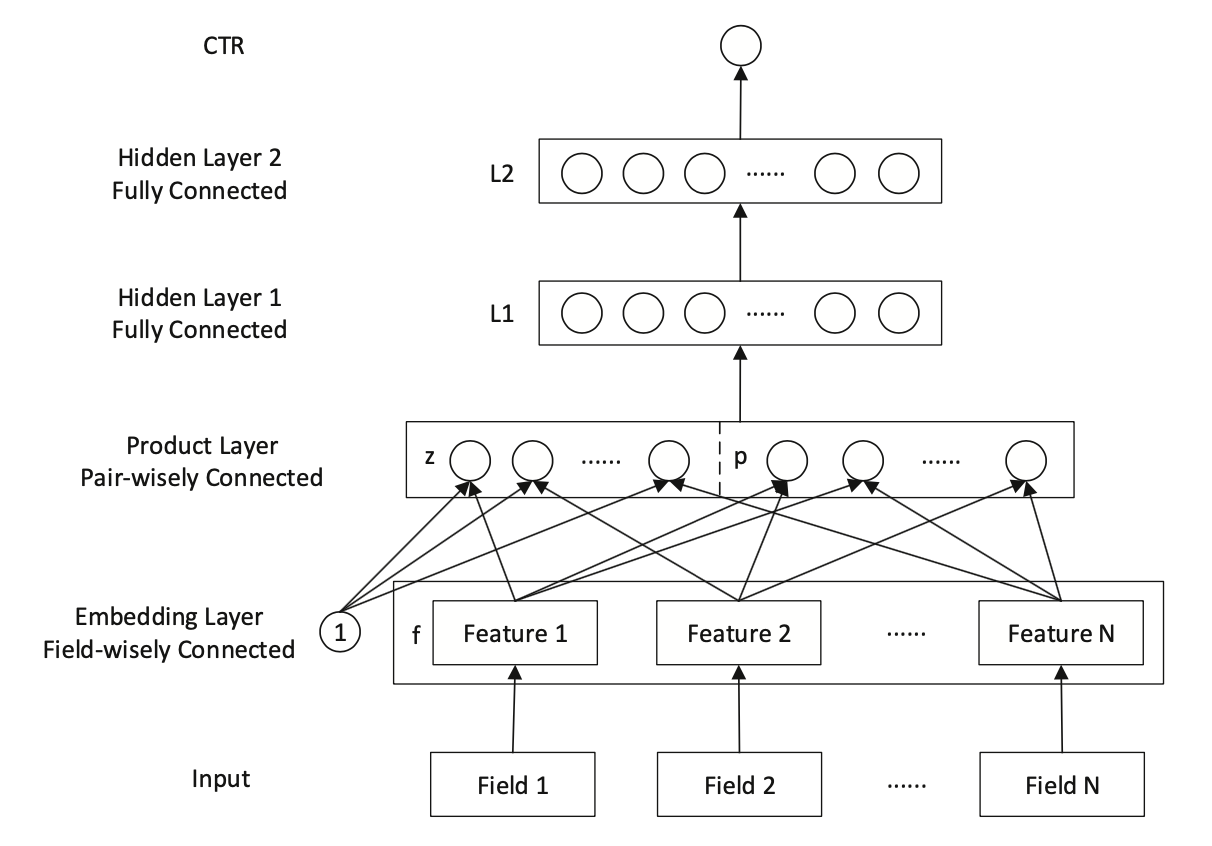
PNN结构显示通过Embedding Lookup得到每个field的Embedding向量，接着将这些向量输入Product Layer，在Product Layer中包含了两部分，一部分是左边的 $z$，就是将特征原始的Embedding向量直接保留；另一部分是右侧的 $p$ ，即对应特征之间的product操作；可以看到PNN相比于FNN一个优势就是保留了原始的低阶embedding特征。

在PNN中，由于引入Product操作，会使模型的时间和空间复杂度都进一步增加。这里以IPNN为例，其中$p$是pair-wise的特征交叉向量，假设我们共有N个特征，每个特征的embedding信息$f_i\in R^M$；在Inner Product的情况下，通过交叉项公式 $g(f_i,f_j)$会得到 $p\in R^{N\times N}$ （其中 [公式] 是对称矩阵），此时从Product层到 [公式] 层（假设 [公式] 层有 [公式] 个结点），对于 [公式] 层的每个结点我们有： $W_p^n\odot p = \sum_{i=1}^N\sum_{j=1}^N(W_p^n)_{i,j}p_{i,j}$，因此这里从product layer到L1层参数空间复杂度为$O(D_1N^2)$ ；作者借鉴了FM的思想对参数 $W_p^n$进行了矩阵分解：$W_p^n=\theta^n\theta^{nT}$ ，此时L1层每个结点的计算可以化简为： $W_p^n\odot p = \sum_{i=1}^N\sum_{j=1}^N\langle\theta_i^n,\theta_j^{n}\rangle\langle f_i,f_j\rangle$ ，空间复杂度退化 $O(D_iNM)$。

优势：

PNN通过$z$保留了低阶Embedding特征信息
通过Product Layer引入更复杂的特征交叉方式，
不足：
计算时间复杂度相对较高