Reading

Deep Generative Models概述

Dec 11, 2024
844 views
Generative Model
#Autoregressive #Generating Model #VAE

简介

如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\)）视为来自底层分布（例如\( p_{data}\)）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\)的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。

我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集\(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。

在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。

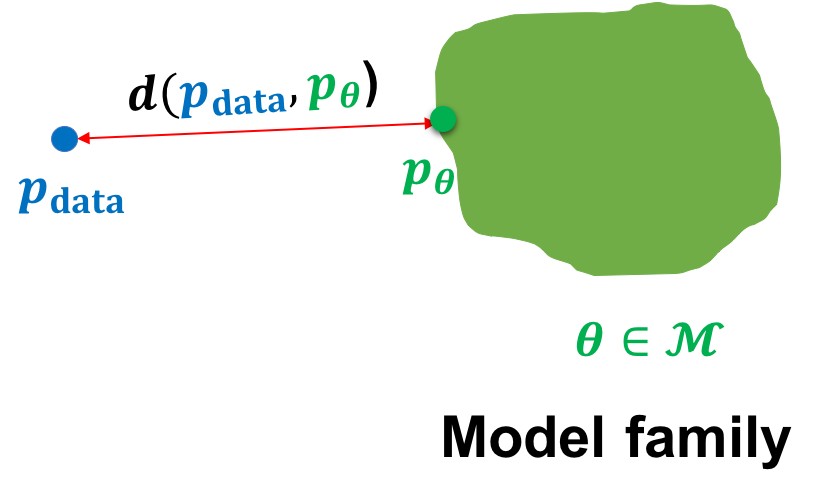
image
image

如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题:

\[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\]

其中，\(d()\)是概率分布之间的距离。

概念定义

  • 生成(Generation)：从真实分布生成数据
  • 推断(Inference)：从数据推断真实分布的参数或结构
  • Prior Knowledge：在Deep Generative Model中的先验
    1. 损失函数(loss function)：如最大似然函数
    2. 参数形式(parametric form)：如假设真实分布服从正态分布
    3. 优化算法(optimization algorithm)

判别式与生成式的区别：

  • 判别式(Discriminative)：对条件概率\(p ( y ∣ x )\) 建模，即在数据的真实分布空间中找出Decision Boundary，给定数据 \( x\) 属于标签 \(y\) 的概率
  • 生成式(Generative)：对联合概率\(p ( x , y )\) 建模，即尝试拟合一个数据与label共存的空间，得同时给定数据 \(x\) 和标签 \(y\)，才能知道概率
  • 由Bayes有\(p(y|x)=\frac{p(x,y)}{p(x)}\)，Discriminative建模对象是\(p ( y ∣ x ) \)(假设了参数结构、loss、优化方式等prior knowledge），所以模型只能接受输入\(x\)。但Generative是对\(p ( x , y )\) 建模，假设了联合分布的prior knowledge，如果知道y，它可以输出\(p(x,y)=p(x|y)p(y)\)；如果知道\(x\)，它也可以输出\(p ( x , y ) = p ( y ∣ x ) p ( x ) \)，所以更全面也更复杂。
  • 于是Discriminative可以看作是一种Data Conditional Generative Model即\(p ( y ∣ x )\) ，这区别于Class Conditional Generative Model即\(p ( x ∣ y ) \)

Deep Generative Model的三大问题

  1. Representation：如何对联合分布 \(p(x,y)\) 进行建模，怎样表示这个模型？
  2. Learning：如何准确地度量真实分布与模型分布的距离？（从而使其更接近）
  3. Inference：如何从观测数据中推断出真实分布的结构或者参数？

自回归

自回归生成模型（Autoregressive Models）

VAE

VAE变分自编码器

Normalizing Flow Model

  • Autoregressive Model：
\[p_\theta(x)=\prod_{i=1}^n p(x_i|x_{<i})\]
  • Variational Autoencode：
\[p_\theta(x)=\int p_\theta(x,z)dz\]
  • Normalizing Flow Model：
\[p_X(x;\theta)=p_Z(f_\theta^{-1}(x))\Big|det\Big(\frac{\partial f^{-1}_\theta(x)}{\partial x}\Big)\Big|\]

由于Normalizing Flow是对复杂分布做了一个transformation即 \(x=f_\theta(z)\)且要求invertible transformation存在即 \(z=f^{-1}_\theta(x)\)，这个约束过于hard，感觉设计出来的Flow实用性不强，从而在此省略其介绍，感兴趣的可看CS 236 Lec7-Lec8的PPT。

Normalizing flow

GAN

Generative Adversarial Networks (GAN)

从Wasserstein距离、对偶理论到WGAN

VQGAN

Diffusion

2020年6月，来自加州大学伯克利分校的一篇题为DDPM去噪扩散概率模型的NeurIPS论文，在更加庞大的数据集上展现出与当时最优的生成对抗网络（GAN）模型相媲美的性能，研究人员方才逐渐领悟到扩散模型在内容创作领域所蕴藏的威力与前景。

回到2020年的十月，斯坦福大学的研究人员Jiaming Song提出了DDIM（Diffusion Denoising Implicit Model），在提升了DDPM采样效率的基础上，仅用50步就能达到1000步采样的效果。DDIM不仅实现了高效率的采样方法，其作为确定性的采样方法还为后续的研究开创了一种类似于GAN Invesion的方法，用于实现各种真实图像的编辑与生成。

接着，来到2021年的二月，OpenAI发布了“Improved Diffusion”：这篇论文提出了后来被广泛采用的Cosine Noise Schedule，Importance sampling，以及Stride Sampling加速采样等技术。

继之而来的，是2021年五月OpenAI所发布的“Classifier Guidance”（亦被称为Guided Diffusion）。这篇论文提出了一项重要的策略，即通过基于分类器的引导来指导扩散模型生成图像。借助其他多项改进，扩散模型首次成功击败了生成领域的巨头“GAN”，同时也为OpenAI的DALLE-2（一个图像和文本生成模型）的发布奠定了基础。

而后，来到2021年的十二月，DDPM的一作发布了“Classifier Free Guidance”：对“Classifier Guidance”进行了改进，使得扩散模型的引导过程仅需使用扩散模型本身，而不再需要依赖分类器进行实现。这一创新极大地丰富了扩散模型的应用范围与灵活性。

stable diffusion和GAN哪个好？

  • Stable diffusion是一种基于随机微分方程的生成方法，它通过逐步增加噪声来扰动原始图像，直到完全随机化。然后，它通过逐步减少噪声来恢复图像，同时使用一个神经网络来预测下一步的噪声分布。Stable Diffusion的优点是可以在连续的潜在空间中生成高质量的图像，而不需要对抗训练或GAN的损失函数。缺点是需要较长的采样时间和较大的模型容量。Stable Diffusion更适合需要高质量和连续性的图像生成任务。
  • GAN是一种基于对抗训练的生成方法，它由一个生成器和一个判别器组成。生成器从一个随机向量中生成图像，判别器从真实数据和生成数据中区分真假。GAN的优点是可以在离散的像素空间中快速生成图像，而且可以通过不同的损失函数和正则化方法来改善生成质量和多样性。GAN的缺点是训练过程可能不稳定，导致模式崩溃或低质量的输出。而且GAN需要仔细调整超参数和损失函数来达到好的效果，这可能很耗时和困难。GAN更适合需要快速和多样性的图像生成任务。
  • 总结如下：Stable diffusion：①训练过程稳定；②可以生成多样性的图像；③适用于图像修复、去噪等任务。④缺点：生成速度相对较慢；GAN：①能生成高质量的图像；②在某些任务上（如图像到图像翻译）表现优秀；③缺点：训练过程可能不稳定，生成的图像多样性不足。
    两种方法的优劣取决于具体的应用场景。

总结对比

生成模型的数据生成过程，可以看成是将一个先验分布的采样点Z变换成数据分布的采样点X的过程。下面这张图是网上流传得比较广的比较各个生成模型联系和区别的示意图（我重新画的），可以清楚地看到各个模型是如何将采样点Z映射到数据X的。

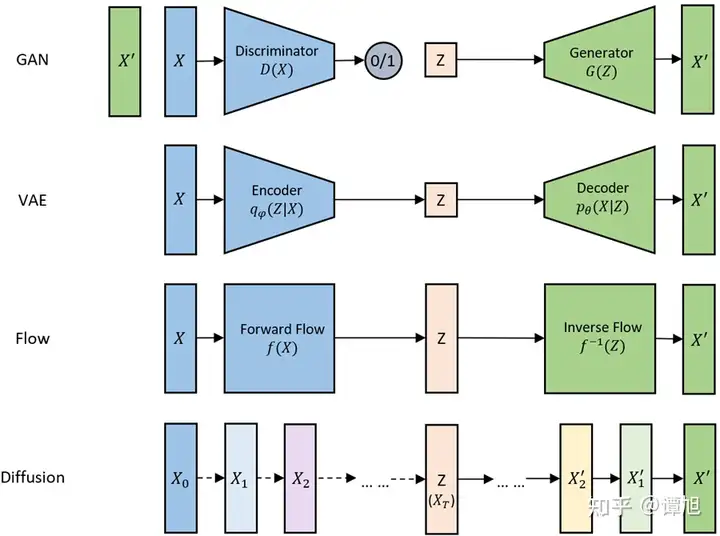
image

现在我们通过一个比喻来说明它们之间的区别。我们把数据的生成过程，也就是从Z映射到X的过程，比喻为过河。河的左岸是Z，右岸是X，过河就是乘船从左岸码头到达右岸码头。船可以理解为生成模型，码头的位置可以理解为样本点Z或者X在分布空间的位置。不同的生成模型有不同的过河的方法，如下图所示（图中小圆点代表样本点，大圆圈代表样本分布，绿色箭头表示loss），我们分别来分析。

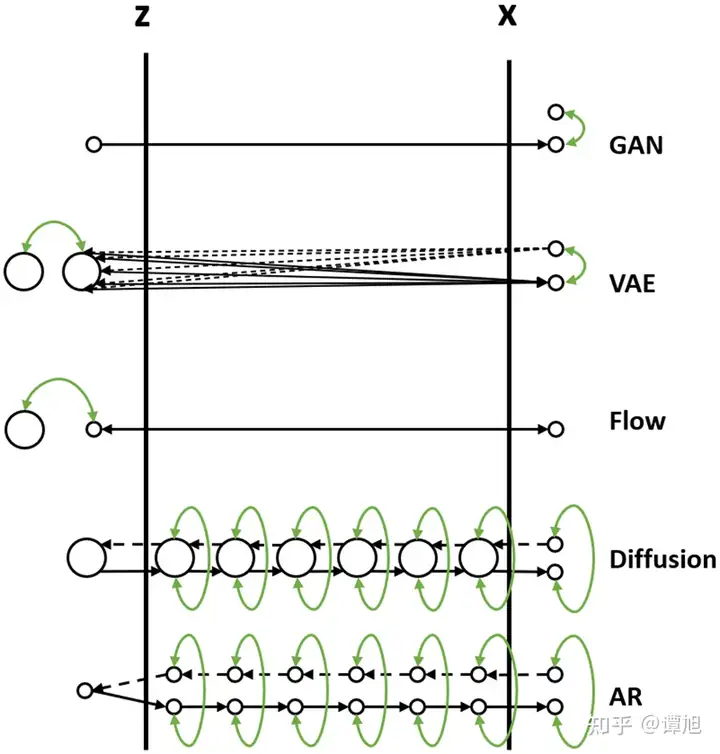
image
  1. GAN的过河方式
    从先验分布随机采样一个Z，也就是在左岸随便找一个码头，直接通过对抗损失的方式强制引导船开到右岸，要求右岸下船的码头和真实数据点在分布层面上比较接近。
  2. VAE的过河方式
    1）VAE在过河的时候，不是强制把河左岸的一个随机点拉到河右岸，而是考虑右岸的数据到达河左岸会落在什么样的码头。如果知道右岸数据到达左岸大概落在哪些码头，我们直接从这些码头出发就可以顺利回到右岸了。
    2）由于VAE编码器的输出是一个高斯分布的均值和方差，一个右岸的样本数据X到达河左岸的码头位置不是一个固定点，而是一个高斯分布，这个高斯分布在训练时会和一个先验分布（一般是标准高斯分布）接近。
    3）在数据生成时，从先验分布采样出来的Z也大概符合右岸过来的这几个码头位置，通过VAE解码器回到河右岸时，大概能到达真实数据分布所在的码头。
  3. Flow的过河方式
    1）Flow的过河方式和VAE有点类似，也是先看看河右岸数据到河左岸能落在哪些码头，在生成数据的时候从这些码头出发，就比较容易能到达河右岸。
    2）和VAE不同的是，对于一个从河右岸码头出发的数据，通过Flow到达河左岸的码头是一个固定的位置，并不是一个分布。而且往返的船开着双程航线，来的时候从什么右岸码头到达左岸码头经过什么路线，回去的时候就从这个左岸码头经过这个路线到达这个右岸码头，是完全可逆的。
    3）Flow需要约束数据到达河左岸码头的位置服从一个先验分布（一般是标准高斯分布），这样在数据生成的时候方便从先验分布里采样码头的位置，能比较好的到达河右岸。
  4. Diffusion的过河方式
    1）Diffusion也借鉴了类似VAE和Flow的过河思想，要想到达河右岸，先看看数据从河右岸去到左岸会在哪个码头下船，然后就从这个码头上船，准能到达河右岸的码头。
    2）但是和Flow以及VAE不同的是，Diffusion不只看从右岸过来的时候在哪个码头下船，还看在河中央经过了哪些桥墩或者浮标点。这样从河左岸到河右岸的时候，也要一步一步打卡之前来时经过的这些浮标点，能更好约束往返的航线，确保到达河右岸的码头位置符合真实数据分布。
    3）Diffusion从河右岸过来的航线不是可学习的，而是人工设计的，能保证到达河左岸的码头位置，虽然有些随机性，但是符合一个先验分布（一般是高斯分布），这样方便我们在生成数据的时候选择左岸出发的码头位置。
    4）因为训练模型的时候要求我们一步步打卡来时经过的浮标，在生成数据的时候，基本上也能遵守这些潜在的浮标位置，一步步打卡到达右岸码头。
    5）如果觉得开到河右岸一步步这样打卡浮标有点繁琐，影响船的行进速度，可以选择一次打卡跨好几个浮标，就能加速船行速度，这就对应diffusion的加速采样过程。
  5. AR的过河方式
    1）可以类比Diffusion模型，将AR生成过程 \(X_0, X_{0:1}, …, X_{0:t}, X_{0:t+1}, …, X_{0:T}\) 看成中间的一个个浮标。从河右岸到达河左岸的过程就好比自回归分解，将 \(X_{0:T}\) 一步步拆解成中间的浮标，这个过程也是不用学习的。
    2）河左岸的码头 \(X_0\) 可以看成自回归生成的第一个START token。AR模型河左岸码头的位置是确定的，就是START token对应的embedding。
    3）在训练过程中，自回归模型也一个个对齐了浮标，所以在生成的时候也能一步步打卡浮标去到河右岸。
    4）和Diffusion不同的是，自回归模型要想加速，跳过某些浮标，就没有那么容易了，除非重新训练一个semi-autoregressive的模型，一次生成多个token跨过多个浮标。
    5）和Diffusion类似的是，在训练过程中都使用了teacher-forcing的方式，以当前步的ground-truth浮标位置为出发点，预测下一个浮标位置，这也降低了学习的难度，所以通常来讲，自回归模型和Diffusion模型训练起来都比较容易。

Reference

CS236 note

CS236 Deep Generative Models

通俗形象地分析比较生成模型（GAN/VAE/Flow/Diffusion/AR）