本文受启发于著名的国外博文《Wasserstein GAN and the Kantorovich-Rubinstein Duality》，内容跟它大体上相同，但是删除了一些冗余的部分，对不够充分或者含糊不清的地方作了补充。

Wasserstein距离

显然，整篇文章必然围绕着Wasserstein距离（\(\mathcal{W}\)距离）来展开。假设我们有了两个概率分布\(p(x),q(x)\)，那么Wasserstein距离的定义为

\[ \mathcal{W}[p,q]=\inf_{\gamma\in \Pi[p,q]} \iint \gamma(\boldsymbol{x},\boldsymbol{y}) d(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{x}d\boldsymbol{y} \]

事实上，这也算是最优传输理论中最核心的定义了。

成本函数

首先\(d(x,y)\)，它不一定是距离，其准确含义应该是一个成本函数，代表着从\(x\)运输到\(y\)的成本。常用的\(d\)是基于\(l\)范数衍生出来的，比如

\[ \Vert\boldsymbol{x}-\boldsymbol{y}\Vert_1,\quad\Vert\boldsymbol{x}-\boldsymbol{y}\Vert_2,\quad \Vert\boldsymbol{x}-\boldsymbol{y}\Vert_2^2 \]

都是常见的选择，其中

\[ \Vert \boldsymbol{x}\Vert_1 = \sum_{i=1}^{n} |x_i|,\quad \Vert \boldsymbol{x}\Vert_2 = \sqrt{\sum_{i=1}^{n} x_i^2} \]

特别指出，其实哪种距离并不是特别重要，因为很多范数都是相互等价的，范数的等价性表明其实最终定义出来的\(\mathcal{W}\)距离都差不多。

成本最小化

然后来看\(γ\)，条件\(γ∈Π[p,q]\)意味着：

\[ \int \gamma(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{y}=p(\boldsymbol{x})\quad\text{且}\quad\int \gamma(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{x}=q(\boldsymbol{y}) \]

这也就是说，\(γ\)是一个联合分布，它的边缘分布就是原来的\(p\)和\(q\)。

事实上\(γ\)就描述了一种运输方案。不失一般性，设\(p\)是原始分布，设\(q\)是目标分布，\(p(x)\)的意思是原来在位置\(x\)处有\(p(x)\)量的货物，\(q(x)\)是指最终\(x\)处要存放的货物量，如果\(p(x)>q(x)\)，那么就要把\(x\)处的一部分货物运到别处，反之，如果\(p(x)<q(x)\)，那么就要从别的地方运一些货物到\(x\)处。而\(γ(x,y)\)的意思是指，要从\(x\)处搬\(γ(x,y)dx\)那么多的东西到\(y\)处。

最后是\(inf\)，这表示下确界，简单来说就是取最小，也就是说，要从所有的运输方案中，找出总运输成本\(∬γ(x,y)d(x,y)dxdy\) 最小的方案，这个方案的成本，就是我们要算的\(\mathcal{W}[p,q]\)。如果将上述比喻中的“货物”换成“沙土”，那么Wasserstein距离就是在求最省力的“搬土”方案了，所以Wasserstein距离也被称为“推土机距离”（Earth Mover's Distance）。

最后改编一张开头提到的国外博文的图片，来展示这个“推土”过程：

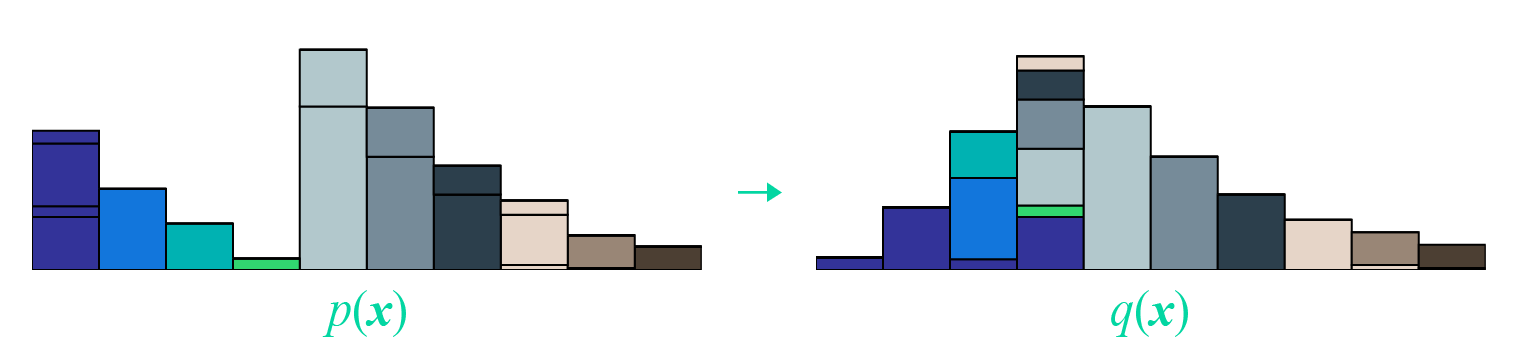
矩阵形式

逐项分析完含义之后，现在我们再来完成地重述一下问题，我们实际上在求

\[ ∬γ(x,y)d(x,y)dxdy \]

的最小值，其中\(d(x,y)\)是事先给定的，而这个最小值要满足如下约束：

\[ \int \gamma(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{y}=p(\boldsymbol{x}),\quad\int \gamma(\boldsymbol{x},\boldsymbol{y}) d\boldsymbol{x}=q(\boldsymbol{y}),\quad \gamma(\boldsymbol{x},\boldsymbol{y})\geq 0 \]

考虑到积分只是求和的极限形式，所以我们可以把\(γ(x,y)\)和\(d(x,y)\)离散化，然后看成很长很长的（列）向量\(Γ\)和\(D\)：

\[ \boldsymbol{\Gamma}=\begin{pmatrix} \gamma(\boldsymbol{x}_1, \boldsymbol{y}_1) \\ \gamma(\boldsymbol{x}_1, \boldsymbol{y}_2) \\ \vdots \\ \hline \gamma(\boldsymbol{x}_2, \boldsymbol{y}_1) \\ \gamma(\boldsymbol{x}_2, \boldsymbol{y}_2) \\ \vdots \\ \hline \vdots \\ \hline \gamma(\boldsymbol{x}_n, \boldsymbol{y}_1) \\ \gamma(\boldsymbol{x}_n, \boldsymbol{y}_2) \\ \vdots \\ \hline \vdots \\ \end{pmatrix},\quad \boldsymbol{D}=\begin{pmatrix} d(\boldsymbol{x}_1, \boldsymbol{y}_1) \\ d(\boldsymbol{x}_1, \boldsymbol{y}_2) \\ \vdots \\ \hline d(\boldsymbol{x}_2, \boldsymbol{y}_1) \\ d(\boldsymbol{x}_2, \boldsymbol{y}_2) \\ \vdots \\ \hline \vdots \\ \hline d(\boldsymbol{x}_n, \boldsymbol{y}_1) \\ d(\boldsymbol{x}_n, \boldsymbol{y}_2) \\ \vdots \\ \hline \vdots \\ \end{pmatrix} \]

相当于就是将\(Γ\)和\(D\)对应位置相乘，然后求和，这不就是内积\(⟨Γ,D⟩\)了吗？

我们可以把约束条件也这样看：把\(p(x),q(x)\)分别看成一个长向量，然后还可以拼起来，把积分也看成求和，这时候约束条件也可以写成矩阵形式\(AΓ=b\)：

\[ \underbrace{\left( \begin{array}{ccc|ccc|c|ccc|c} 1 & 1 & \dots & 0 & 0 & \dots & \dots & 0 & 0 & \dots & \dots \\ 0 & 0 & \dots & 1 & 1 & \dots & \dots & 0 & 0 & \dots & \dots \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \ddots & \vdots & \vdots & \ddots & \ddots \\ 0 & 0 & \dots & 0 & 0 & \dots & \dots & 1 & 1 & \dots & \dots \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \ddots & \vdots & \vdots & \ddots & \ddots \\ \hline 1 & 0 & \dots & 1 & 0 & \dots & \dots & 1 & 0 & \dots & \dots \\ 0 & 1 & \dots & 0 & 1 & \dots & \dots & 0 & 1 & \dots & \dots \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \ddots & \vdots & \vdots & \ddots & \ddots \\ 0 & 0 & \dots & 0 & 0 & \dots & \dots & 0 & 0 & \dots & \dots \\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \ddots & \vdots & \vdots & \ddots & \ddots \\ \end{array} \right)}_{\Large\boldsymbol{A}}\,\, \underbrace{\begin{pmatrix} \gamma(\boldsymbol{x}_1, \boldsymbol{y}_1) \\ \gamma(\boldsymbol{x}_1, \boldsymbol{y}_2) \\ \vdots \\ \hline \gamma(\boldsymbol{x}_2, \boldsymbol{y}_1) \\ \gamma(\boldsymbol{x}_2, \boldsymbol{y}_2) \\ \vdots \\ \hline \vdots \\ \hline \gamma(\boldsymbol{x}_n, \boldsymbol{y}_1) \\ \gamma(\boldsymbol{x}_n, \boldsymbol{y}_2) \\ \vdots \\ \hline \vdots \\ \end{pmatrix}}_{\Large\boldsymbol{\Gamma}} \,\,=\,\, \underbrace{\begin{pmatrix} p(\boldsymbol{x}_1) \\ p(\boldsymbol{x}_2) \\ \vdots \\ p(\boldsymbol{x}_n) \\ \vdots \\ \hline q(\boldsymbol{y}_1) \\ q(\boldsymbol{y}_2) \\ \vdots \\ q(\boldsymbol{y}_n) \\ \vdots \\ \end{pmatrix}}_{\Large\boldsymbol{b}} \]

最后不能忘记的是\(Γ≥0\)，它表示\(Γ\)的每个分量都大于等于0。

线性规划问题

现在问题可以用一行字来描述

\[ \min_{\boldsymbol{\Gamma}}\big\{\langle\boldsymbol{\Gamma},\boldsymbol{D}\rangle\,\big|\,\boldsymbol{A}\boldsymbol{\Gamma}=\boldsymbol{b},\,\boldsymbol{\Gamma}\geq 0\big\} \]

这就是“线性约束下的线性函数最小值”的问题，它就是我们在高中时就已经接触过的线性规划问题了～可见，虽然原始问题足够复杂，又有积分又有下确界的，但经过转写，它本质上就是一个并不难理解的线性规划问题（当然，“不难理解”并不意味着“容易求解”）。

线性规划与对偶

让我们用更一般的记号，把线性规划问题重写一遍，常见的形式有两种：

\[ \min_{\boldsymbol{x}}\big\{\boldsymbol{c}^{\top}\boldsymbol{x}\,\big|\,\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b},\,\boldsymbol{x}\geq 0\big\}\quad\text{或}\quad \min_{\boldsymbol{x}}\big\{\boldsymbol{c}^{\top}\boldsymbol{x}\,\big|\,\boldsymbol{A}\boldsymbol{x}\geq \boldsymbol{b},\,\boldsymbol{x}\geq 0\big\} \]

这两种形式本质上是等价的，只不过在讨论第一种的时候相对简单一点

注意，为了避免混乱，我们必须声明一下各个向量的大小。我们假设每个向量都是列向量，经过转置之后就代表一个行向量，\(x,c∈ℝ^n\)都是n维向量，其中\(c\)也就是权重，\(c^⊤x\)就是对\(x\)的各个分量加权求和；\(b∈ℝ^m\)是m维向量，自然\(A∈ℝ^{m×n}\)是一个\(m×n\)的矩阵了，\(Ax=b\)实际上就是描述了m个等式约束。

弱对偶形式

在规划和优化问题中，“对偶形式”是一个非常重要的概念。一般情况下，“对偶”是指某种变换，能将原问题转化为一个等价的、但是看起来几乎不一样的新问题，即

\[ \text{原问题}\quad\xrightarrow{\text{对偶变换}}\quad \text{新问题} \]

“对偶”之所以称为“对偶”，是因为将新问题进行同样形式的变换后，通常来说能还原为原问题，即

\[ \text{新问题}\quad\xrightarrow{\text{对偶变换}}\quad \text{原问题} \]

即“对偶”像是一面镜子，原问题和新问题相当于“原像”和“镜像”，解决了一个问题，就等价于解决了另一个问题。所以就看哪个问题更简单了。

读者可能还有疑问：“对偶”跟数学中诸如“逆否命题”之类的等价描述有什么区别？其实也没有本质区别，简单来说“对偶”和“逆否命题”都是跟原来的命题完全等价的，但是“对偶”看起来跟原命题很不一样，而“逆否命题”仅仅是原命题的一个逻辑变换～从线性代数的角度来看，“对偶”相当于向量空间中的“原空间”和“补空间”之间的关系。

最大 vs 最小

这里我们先介绍“弱对偶形式”，其实它推导起来还是挺简单的。

我们的目标是\(\min\limits_{\boldsymbol{x}}\big\{\boldsymbol{c}^{\top}\boldsymbol{x}\,\big|\,\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b},\,\boldsymbol{x}\geq 0\big\}\)，设置最小值在\(\boldsymbol{x}^*\)处取到，那么我们有\(\boldsymbol{A}\boldsymbol{x}^*=\boldsymbol{b}\)，我们可以在两边乘以一个\(\boldsymbol{y}^{\top}\in\mathbb{R}^m\)，使得等式变成一个标量：\(\boldsymbol{y}^{\top}\boldsymbol{A}\boldsymbol{x}^*=\boldsymbol{y}^{\top}\boldsymbol{b}\)。

如果此时假设\(\boldsymbol{y}^{\top}\boldsymbol{A}\leq \boldsymbol{c}^{\top}\)，那么\(\boldsymbol{y}^{\top}\boldsymbol{A}\boldsymbol{x}^*\leq \boldsymbol{c}^{\top}\boldsymbol{x}^*\)（因为\(\boldsymbol{x}^* \geq 0\)），则\(\boldsymbol{y}^{\top}\boldsymbol{b}\leq \boldsymbol{c}^{\top} \boldsymbol{x}^*\)。也就是说，在条件\(\boldsymbol{y}^{\top}\boldsymbol{A}\leq \boldsymbol{c}^{\top}\)下的任意\(\boldsymbol{y}^{\top}\boldsymbol{b}\)总是不大于\(\min\limits_{\boldsymbol{x}}\big\{\boldsymbol{c}^{\top}\boldsymbol{x}\,\big|\,\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b},\,\boldsymbol{x}\geq 0\big\}\)，“总是”意味着即使对于最大也一样，所以我们就有

\[ \max_{\boldsymbol{y}}\big\{\boldsymbol{b}^{\top}\boldsymbol{y}\,\big|\,\boldsymbol{A}^{\top}\boldsymbol{y}\leq \boldsymbol{c}\big\}\leq \min_{\boldsymbol{x}}\big\{\boldsymbol{c}^{\top}\boldsymbol{x}\,\big|\,\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b},\,\boldsymbol{x}\geq 0\big\} \]

这便称为“弱对偶形式”，它的形式就是：“左边的最大”还大不过“右端的最小”。

几点评注

对于弱对偶形式，也许下面几点值得进一步说明一下：

1、现在我们将原来的最小值问题变成了一个最大值问题\(\max\limits_{\boldsymbol{y}}\big\{\boldsymbol{b}^{\top}\boldsymbol{y}\,\big|\,\boldsymbol{A}^{\top}\boldsymbol{y}\leq \boldsymbol{c}\big\}\)，这便有了对偶的味道。当然，弱对偶形式之所以“弱”，是因为我们目前找到的对偶形式只是原来问题的一个下界，还没有证明它们二者相等。
2、弱对偶形式在很多优化问题中（包括非线性优化）都成立。如果二者真的相等，那么就是真正意义上的对偶了，称为强对偶形式。
3、理论上，我们确实需要证明上式左右两端相等才能进一步应用它。但从应用角度，其实弱对偶形式给出的下界都已经够用了，因为深度学习中的问题都很复杂，能有一个近似的目标去优化都已经很不错了。
4、读者可能会想问：前面我们为什么要假设\(\boldsymbol{y}^{\top}\boldsymbol{A}\leq \boldsymbol{c}^{\top}\)而不干脆假设\(\boldsymbol{y}^{\top}\boldsymbol{A}= \boldsymbol{c}^{\top}\)？假设后者当然简单很多，但问题是后者在实践中很难实现，所以只能假设前者。

强对偶形式

上面已经说了，从实践角度其实弱对偶形式已经够用了。但是为了让对完整理论有兴趣的读者也有更多收获，这里继续把“强对偶形式”也论证一番。对于只关心WGAN本身的读者来说，可以考虑跳过这部分。

所谓强对偶形式，也就是

\[ \max_{\boldsymbol{y}}\big\{\boldsymbol{b}^{\top}\boldsymbol{y}\,\big|\,\boldsymbol{A}^{\top}\boldsymbol{y}\leq \boldsymbol{c}\big\} = \min_{\boldsymbol{x}}\big\{\boldsymbol{c}^{\top}\boldsymbol{x}\,\big|\,\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b},\,\boldsymbol{x}\geq 0\big\} \]

注意前面已经说了，弱对偶形式对于很多优化问题都成立，但强对偶形式不一定成立。而对于线性规划来说，强对偶形式是成立的。

Farkas引理

强对偶形式的证明，主要用到称之为“Farkas引理”的结论：

对于固定的矩阵\(A∈ℝ^{m×n}\)和向量\(b∈ℝ^m\)，下面两个选项有且只有一个成立：
1、存在\(x∈ℝ^n\)且\(x≥0\)，使得\(Ax=b\)；
2、存在\(y∈ℝ^m\)使得\(A^⊤y≤0\)且\(b^⊤y>0\)。

什么鬼？又大又小又转置的？能不能说人话？

现在我们随便给定一个向量b，那么显然它只有两种可能性，而且必有一种成立：1、在锥内（包括边界）；2、在锥外。

如果它在锥内，那么根据锥本身的定义，它就可以表示为\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n\)的非负线性组合（表示方式可能不唯一），也就是存在\(x≥0\)，使得\(Ax=b\)，这就是第一种情况。

如果在锥外呢？怎么表示在锥外？当然我们可以直接写出锥内的否命题，但是那实用价值不大。如果向量b 在锥外，那么我们总是可以找到一个“标杆”向量y，它与a1,a2,…,an的夹角都大于等于90度，向量表示法就是内积都小于等于零，即\((\boldsymbol{a}_1^{\top}\boldsymbol{y}, \boldsymbol{a}_2^{\top}\boldsymbol{y}, \dots, \boldsymbol{a}_n^{\top}\boldsymbol{y}) \leq 0\)，或者写成一个整体\(A^⊤y≤0\)。找到这个“标杆”后，向量b与“标杆”的夹角必然是要小于90度的，即\(b^⊤y>0\)。这样一个大于等于90度，一个小于90度，保证了向量b在全体向量构成的锥外。这就是第二种情况。

当然，这不能算是完备的证明，只能算是一个启发式引导，完备的证明还要仔细论证为什么这些向量的非负线性组合构成了一个锥～这些就不在本文的范畴了。Farkas引理的特点是二选一，比如我要证明满足第二点，只需要证明它不满足第一点，反之亦然。这是对问题的一个转化。

从引理到强对偶

有了Farkas引理，我们就可以证明强对偶形式了。证明的思路是：证明max可以任意程度地接近min。

证明还是先假设min的最小值在\(x^∗\)处取到，即最小值为\(z^* = \boldsymbol{c}^{\top}\boldsymbol{x}^*\)，那么我们考虑：

\[ \hat{\boldsymbol{A}} = \begin{pmatrix} \boldsymbol{A} \\ -\boldsymbol{c}^{\top} \end{pmatrix}, \quad \hat{\boldsymbol{b}}_{\epsilon} = \begin{pmatrix} \boldsymbol{b} \\ -z^* + \epsilon \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} \boldsymbol{y} \\ \alpha \end{pmatrix} \]

当\(ϵ>0\)时，那么对于任意x≥0，\(\hat{\boldsymbol{A}} \boldsymbol{x}\)都不可能等于\(\hat{\boldsymbol{b}}_{\epsilon}\)，这是因为\(\boldsymbol{c}^{\top} \boldsymbol{x}^* = z^*\)已经是最小值，所以\(−z^∗\)是\(−c^⊤x\)能达到的最大值，它不可能等于更大的\(−z^∗+ϵ\)。

前面已经说了，不满足第一种情况，那就只能满足第二种情况了，即存在\(\hat{\boldsymbol{y}} = \begin{pmatrix} \boldsymbol{y} \\ \alpha \end{pmatrix}\)使得\(\hat{\boldsymbol{A}}^{\top}\hat{\boldsymbol{y}}\leq 0\)且\(\hat{\boldsymbol{b}}_{\epsilon}^{\top}\hat{\boldsymbol{y}} > 0\)，这等价于

\[ \boldsymbol{A}^{\top} \boldsymbol{y} \leq \alpha \boldsymbol{c}, \quad \boldsymbol{b}^{\top} \boldsymbol{y} > \alpha(z^* - \epsilon) \]

下面我们表明\(α\)必须大于0，这是因为\(0 < \hat{\boldsymbol{b}}_{\epsilon}^{\top}\hat{\boldsymbol{y}} = \hat{\boldsymbol{b}}_{0}^{\top}\hat{\boldsymbol{y}} + \alpha\epsilon\)，所以我们再去考虑\(ϵ=0\)。而当\(ϵ=0\)时有\(\hat{\boldsymbol{A}} \boldsymbol{x}^* = \hat{\boldsymbol{b}}_0\)，即满足Farkas引理的第一种情况，那就不满足第二种情况，而不满足第二种情况，意味着“\(\forall \hat{\boldsymbol{A}}^{\top}\hat{\boldsymbol{y}}\leq 0,\,\text{都有}\hat{\boldsymbol{b}}_{0}^{\top}\hat{\boldsymbol{y}}\leq 0\)”，刚刚我们已经证明了\(\hat{\boldsymbol{b}}_{0}^{\top}\hat{\boldsymbol{y}} + \alpha\epsilon > 0\)，所以必须有\(α\)>0

现在确定\(α>0\)，我们就可以得到

\[ \boldsymbol{A}^{\top} \big(\boldsymbol{y}/\alpha\big) \leq \boldsymbol{c}, \quad \boldsymbol{b}^{\top} \big(\boldsymbol{y}/\alpha\big) > z^* - \epsilon \]

这意味着

\[ \max_{\boldsymbol{y}}\big\{\boldsymbol{b}^{\top}\boldsymbol{y}\,\big|\,\boldsymbol{A}^{\top}\boldsymbol{y}\leq \boldsymbol{c}\big\} > z^* - \epsilon \]

而弱对偶形式已经告诉我们

\[ z^* \geq \max_{\boldsymbol{y}}\big\{\boldsymbol{b}^{\top}\boldsymbol{y}\,\big|\,\boldsymbol{A}^{\top}\boldsymbol{y}\leq \boldsymbol{c}\big\} \]

也就是\(\max\limits_{\boldsymbol{y}}\big\{\boldsymbol{b}^{\top}\boldsymbol{y}\,\big|\,\boldsymbol{A}^{\top}\boldsymbol{y}\leq \boldsymbol{c}\big\}\)被夹在\(z^∗−ϵ\)和\(z^∗\)之间，而因为\(ϵ>0\)是任意的，所以两者可以无限接近，从而

\[ \max_{\boldsymbol{y}}\big\{\boldsymbol{b}^{\top}\boldsymbol{y}\,\big|\,\boldsymbol{A}^{\top}\boldsymbol{y}\leq \boldsymbol{c}\big\}=z^*=\min_{\boldsymbol{x}}\big\{\boldsymbol{c}^{\top}\boldsymbol{x}\,\big|\,\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b},\,\boldsymbol{x}\geq 0\big\} \]

这便是要证的强对偶形式。

Wasserstein GAN

好了，进行了一大通的准备工作后，我们终于可以导出Wasserstein GAN了，就本文来看，它只不过是线性规划的对偶形式的一个副产品罢了。

W距离的对偶

在推导之前，我们还是再来捋一捋本文的思路：本文先给出了\(\mathcal{W}\)距离的定义，然后经过分析，发现它其实就是普通线性规划问题的一个连续版本；因此中间我们花了相当一部分篇幅去学习线性规划及其对偶形式，最终得到了结论。

现在我们要做的事情，就是把整个过程“逆”过来，也就是将找出对应的连续版本，为\(\mathcal{W }\)距离找一个对偶表达式。

其实这个过程也不复杂，由结论，我们得到

\[ \min_{\boldsymbol{\Gamma}}\big\{\langle\boldsymbol{\Gamma},\boldsymbol{D}\rangle\,\big|\,\boldsymbol{A}\boldsymbol{\Gamma}=\boldsymbol{b},\,\boldsymbol{\Gamma}\geq 0\big\}=\max_{\boldsymbol{F}}\big\{\langle\boldsymbol{b},\boldsymbol{F}\rangle\,\big|\,\boldsymbol{A}^{\top}\boldsymbol{F}\leq \boldsymbol{D}\big\} \]

注意式b是由两部分拼起来的，所以我们也可以把F类似地写成：

\[ \boldsymbol{F}=\begin{pmatrix} f(\boldsymbol{x}_1) \\ f(\boldsymbol{x}_2) \\ \vdots \\ f(\boldsymbol{x}_n) \\ \vdots \\ \hline g(\boldsymbol{y}_1) \\ g(\boldsymbol{y}_2) \\ \vdots \\ g(\boldsymbol{y}_n) \\ \vdots \\ \end{pmatrix} \]

现在\(⟨b,F⟩\)可以写成

\[ \langle\boldsymbol{b},\boldsymbol{F}\rangle=\sum_n p(\boldsymbol{x}_n) f(\boldsymbol{x}_n) + \sum_n q(\boldsymbol{x}_n) g(\boldsymbol{x}_n) \]

或者对应的积分形式是

\[ \langle\boldsymbol{b},\boldsymbol{F}\rangle=\int \big[p(\boldsymbol{x}) f(\boldsymbol{x}) + q(\boldsymbol{x}) g(\boldsymbol{x})\big]d\boldsymbol{x} \]