简介

生成对抗网络 (Generative Adversarial Network, GAN) 是由 Goodfellow 于 2014 年提出的一种对抗网络。这个网络框架包含两个部分，一个生成模型 (generative model) 和一个判别模型 (discriminative model)。其中，生成模型可以理解为一个伪造者，试图通过构造假的数据骗过判别模型的甄别；判别模型可以理解为一个警察，尽可能甄别数据是来自于真实样本还是伪造者构造的假数据。两个模型都通过不断的学习提高自己的能力，即生成模型希望生成更真的假数据骗过判别模型，而判别模型希望能学习如何更准确的识别生成模型的假数据。

网络框架

GAN 由两部分构成，一个生成器 (Generator) 和一个判别器 (Discriminator)。对于生成器，我们需要学习关于数据 \(x\) 的一个分布 \(p_g\)，首先定义一个输入数据的先验分布 \(p_z(z)\)，其次定义一个映射 \(G \left(\boldsymbol{z}; \theta_g\right): \boldsymbol{z} \to \boldsymbol{x}\)。对于判别器，我们则需要定义一个映射 \(D \left(\boldsymbol{x}; \theta_d\right)\) 用于表示数据 \(x\) 是来自于真实数据，还是来自于 \(p_g\)。GAN 的网络框架如下图所示 2：

模型训练

Goodfellow 在文献中给出了一个重要的公式用于求解最优的生成器

上式中，在给定的 \(G\) 的情况下，\(\max_{D} V\left(G, D\right)\) 衡量的是 \(p_{data}\) 和 \(p_g\) 之间的“区别”，因此我们最终的优化目标就是找到最优的 \(G^*\) 使得  \(p_{data}\) 和 \(p_g\) 之间的“区别”最小。

首先，在给定 \(G\) 的时候，我们可以通过最大化 \(V \left(G, D\right)\) 得到最优 \(D^*\)

对于给定的任意 \(a, b \in \mathbb{R}^2 \setminus \{0, 0\}\)，\(a \log\left(x\right) + b \log\left(1 - x\right)\)在 \(x = \dfrac{a}{a+b}\) 处取得最大值，\(D\) 的最优值为

因此，\(\max_{D} V \left(G, D\right)\) 可重写为

其中 KL 表示 KL 散度 ，JS 表示 JS 散度，因此在全局最优情况下 \(p_g = p_{data}\)。

整个 GAN 的训练过程如下所示：

在实际的训练过程中，我们通常不会直接训练 \(G\) 最小化 \(\log \left(1 - D \left(G \left(\boldsymbol{z}\right)\right)\right)\)，因为其在学习过程中的早起处于饱和状态，因此我们通常会通过最大化\(\log \left(D \left(G \left(\boldsymbol{z}\right)\right)\right)\)。

存在的问题

针对 GAN，包括 Goodfellow 自己在内也提出了其中包含的很多问题，因此后人也提出了大量的改进，衍生出了大量的 GAN 变种。本章节仅对原始的 GAN 中存在的问题进行简略介绍，相关的改进请参见后续的具体改进算法。

JS 散度问题

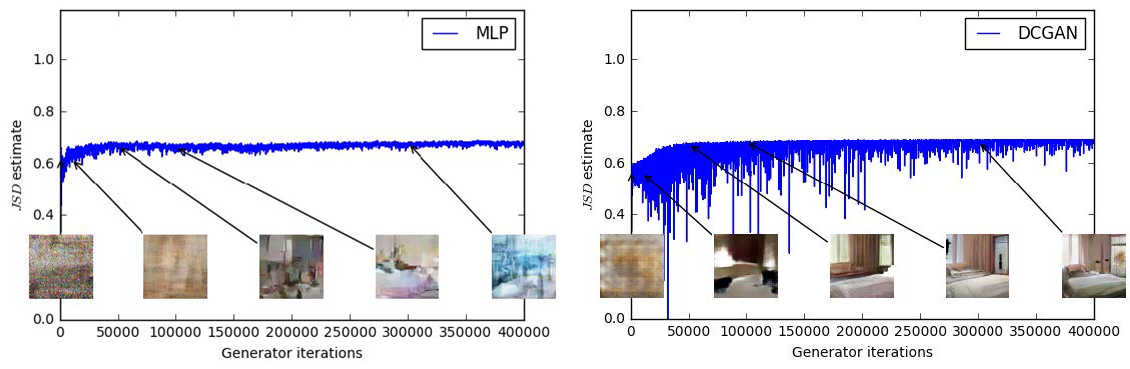
我们在训练判别器的时候，其目标是最大化 JS 散度，但 JS 散度真的能够很好的帮助我们训练判别器吗？ Wasserstein GAN 一文 给出了不同生成器情况下 JS 散度的变化情况。

上图中，左边为一个基于 MLP 的生成器，右边为一个 DCGAN 生成器，两者均有一个 DCGAN 的判别器。根据上文我们可以知道判别器的目标是最大化

上图中 Y 轴绘制的为 \(\dfrac{1}{2} L \left(D, \theta_g\right) + \log 2\)，因为\(-2 \log 2 \leq L \left(D, \theta_g\right) \leq 0\)，因此我们可得\(0 \leq \dfrac{1}{2} L \left(D, \theta_g\right) + \log 2 \leq \log 2\)。从图中我们可以看出，针对两种不同的情况，其值均很快的逼近最大值 log⁡2≈0.69，当接近最大值的时候，判别器将具有接近于零的损失，此时我们可以发现，尽管 JS 散度很快趋于饱和，但 DCGAN 生成器的效果却仍在不断的变好，因此，使用 JS 散度作为判别其的目标就显得不是很合适。

多样性问题 Mode Collapse

Mode Collapse 问题是指生成器更多的是生成了大量相同模式的数据，导致的结果就是生成的数据缺乏多样性，如下图所示:

不难看出，其中红色方框圈出来的图像十分相似，这样的问题我们就称之为 Mode Collapse。Goolfellow 曾经从不同的 KL 散度的角度解释引起 Mode Collapse 的问题，但最后发现其并非由散度的不同所导致。对于 KL 散度，其并非是对称的，即\(D_{KL} \left(p_{data} \Vert p_{model}\right)\)与 \(D_{KL} \left(p_{model} \Vert p_{data}\right)\) 是不同的。在最大化似然估计的时候使用的是前者，而在最小化 JS 散度的时候使用的更类似于后者。如下图所示

假设我们的模型 q 并没有足够能能力去拟合真实数据分布 p，假设真实数据由两个二维的高斯分布构成，而模型需要使用一个一维的高斯分布去拟合。在左图中，模型更倾向于覆盖两个高斯分布，也就是说其更倾向与在有真实数据的地方得到更大的概率。在右图中，模型更倾向于覆盖其中一个高斯分布，也就是说其更倾向于在没有真实数据的地方取得更小的概率。这样，如果我们用 JS 散度训练模型的时候就容易出现模式缺失的问题，但尽管我们利用前者去优化模型，但结果中仍然出现了 Mode Collapse 的问题，这也就说明并非 JS 散度问题导致的 Mode Collapse。

针对 Mode Collapse 的问题，出现了大量不同角度的优化

• 基于正则化的优化
• 基于 Minibatch 的优化
• 基于 Unrolled Optimization 的优化
• 基于集成算法的优化

MNIST 示例

我们利用 MNIST 数据集测试原始的 GAN 模型的效果，代码主要参考了 Keras-GAN，最终实现代码详见 image_gan_keras.py，我们简单对其核心部分进行说明。

• 生成器
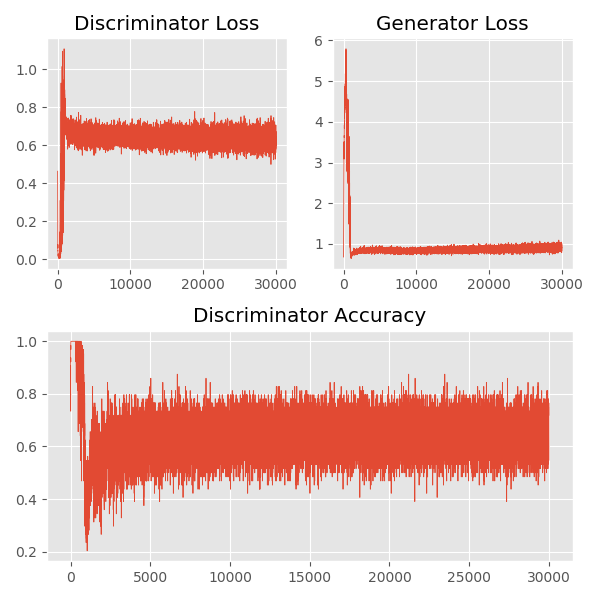
  在生成器中，我们使用了一个包含3个隐含层的全链接网络，其中 self._hidden_dim 是我们定义的隐含节点最多一层的节点数；self._noise_shape 为用于生成器的噪音数据的形状；self._input_shape 为输入数据形状，即图片数据的形状，中间层次采用的激活函数为 LeakyReLU，最后一层采用的激活函数为 tanh。

• 判别器
  在判别器中，我们使用了一个包含2个隐含层的全链接网络，中间层次采用的激活函数为 LeakyReLU，最后一层采用的激活函数为 sigmoid。

• 对抗网络
  在构造整个对抗网络的时候，需要注意我们训练完判别器后，通过训练整个对抗网络进而训练生成器的时候是固定住训练好的判别器的，因此在训练整个对抗网络的时候我们应该将判别器置为无需训练的状态。

• 训练过程
  在训练整个对抗网络的时候，我们对于一个给定的生成器，我们将生成器生成的数据作为负样本，将从真实数据中采样的数据作为正样本训练判别器。Goodfellow 在描述 GAN 训练的过程中，对于给定的生成器，训练判别器 k 次，不过通常取 k=1。训练好判别器后，再随机生成噪音数据用于训练生成器，周而复始直至达到最大迭代次数。

在整个训练过程中，我们分别记录了判别器和生成器的损失的变化，以及判别器的准确率的变化，如下图所示：

从上图中我们可以看出，在训练开始阶段，判别器能够相对容易的识别出哪些数据是来自于真实数据的采样，哪些数据是来自于生成器的伪造数据。随着训练的不断进行，判别器的准确率逐渐下降，并稳定在 60% 左右，也就是说生成器伪造的数据越来越像真实的数据，判别器越来越难进行甄别。

下图中我们展示了利用 MNIST 数据集，进行 30000 次的迭代，每 1000 次截取 100 张生成器利用相同噪音数据伪造的图像，最后合成的一张生成图片的变化动图。

Reference

生成对抗网络简介 (GAN Introduction)