INCOMING TRANSMISSION

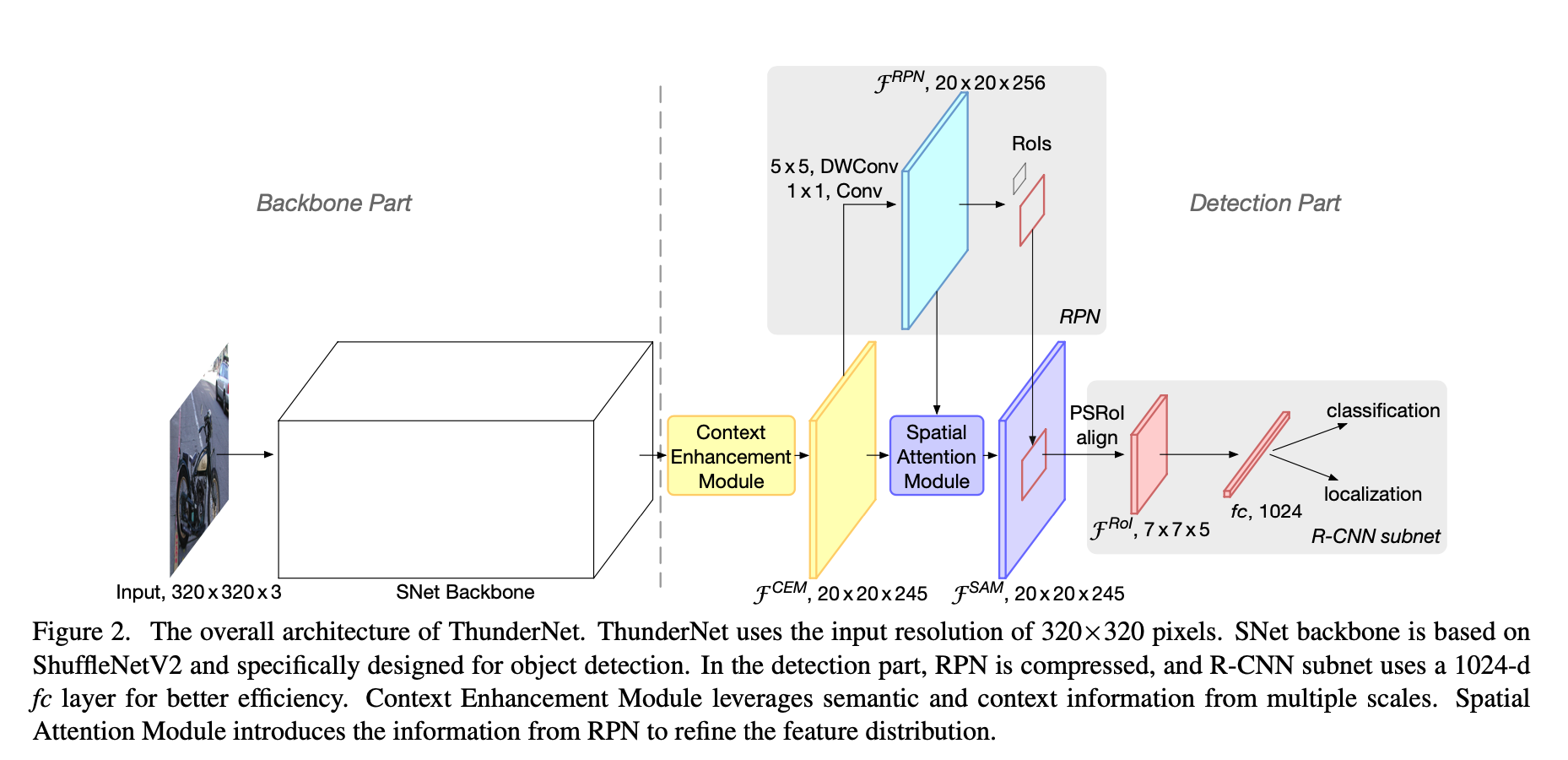
网络整体介绍 ThunderNet的整体架构如下图所示。 ThunderNet使用320×320像素作为网络的输入分辨率。整体的网络结构分为两部分：Backbone部分和Detection部分。网络的骨干部分为SNet，SNet是基于ShuffleNetV2进行修改得到的。 网络的检测部分，利用了压缩的RPN网络，修改自LightHead RCNN网络用以提高效率。 并提出Context Enhancement Module整合局部和全局特征增强网络特征表达能力。 并提出Spatial Attention Module空间注意模块，引入来自RPN的前后景信息用以优化特征分布。 backbone 部分 1.输入分辨率 为了加快推理（前向操作）速度，作者使用320320大小的输入图像。需要注意的...

1. 什么是NGram模型 NGram是一种基于统计语言模型的算法。它的基本思想是将文本里面的内容按照字节进行大小为N的滑动窗口操作，形成了长度是N的字节片段序列。 每一个字节片段称为gram，对所有gram的出现频度进行统计，并且按照事先设定好的阈值进行过滤，形成关键gram列表，也就是这个文本的向量特征空间，列表中的每一种gram就是一个特征向量维度。 该模型基于这样一种假设，第N个词的出现只与前面N1个词相关，而与其它任何词都不相关，整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。常用的是二元的BiGram和三元的TriGram。 说完了ngram模型的概念之后，下面讲解ngram的一般应用。 2. NGram模型用于评估语句是否合理 如果...

问题背景 首先简化一下问题，本文所讨论的多模态，主要指图文混合的双模态，即输入和输出都可以是图文。可能有不少读者的第一感觉是：多模态模型难道不也是烧钱堆显卡，Transformer“一把梭”，最终“大力出奇迹”吗？ 其实没那么简单。先看文本生成，事实上文本生成自始至终都只有一条主流路线，那就是语言模型，即建模条件概率 [Math] ，不论是最初的 ngram语言模型，还是后来的Seq2Seq、GPT，都是这个条件概率的近似。也就是说，一直以来，人们对“实现文本生成需要往哪个方向走”是很明确的，只是背后所用的模型有所不同，比如LSTM、CNN、Attention乃至最近复兴的线性RNN等。所以，文本生成确实可以All in Transformer来大力出奇迹，因为方向是标准的、清晰的。 然而，...

词向量，英文名叫Word Embedding，按照字面意思，应该是词嵌入。说到词向量，不少读者应该会立马想到Google出品的Word2Vec，大牌效应就是不一样。另外，用Keras之类的框架还有一个Embedding层，也说是将词ID映射为向量。由于先入为主的意识，大家可能就会将词向量跟Word2Vec等同起来，而反过来问“Embedding是哪种词向量？”这类问题，尤其是对于初学者来说，应该是很混淆的。事实上，哪怕对于老手，也不一定能够很好地说清楚。 这一切，还得从one hot说起... 五十步笑百步 one hot，中文可以翻译为“独热”，是最原始的用来表示字、词的方式。为了简单，本文以字为例，词也是类似的。假如词表中有“科、学、空、间、不、错”六个字，one hot就是给这六个字分...

1. 检测任务的困难 图像分类算法，比如ResNeXt101 32 × 48d网络结构，在Imagenet数据集上的Top5准确率已经98%左右，Top1为85%。对于图像检测算法，最好的模型在coco数据集上的效果 AP_{50} 为62%，显然，总体上来看，准确率差了20个点左右，那么问题来了，为什么检测算法比识别算法的效果低这么多呢？ 1.1 尺度差异 作者认为原因在于，检测任务中的目标存在较大的尺度变化（large scale variation）。作者统计了Imagenet和COCO数据集的特点，如下图， 其中，横坐标表示目标相对于原图的比例，纵坐标表示累计分布（cumulation distribution function）。显然，由图中可以看出，COCO数据集中50%的目标相...

FPN 1.结构区别 （a）图片金字塔生成特征金字塔：缩放图片比例 （b）通常的CNN网络结构 （c）多尺度特征融合的方式：像SSD（Single Shot Detector）就是采用这种多尺度特征融合的方式，没有上采样过程，即从网络不同层抽取不同尺度的特征做预测，这种方式不会增加额外的计算量。作者认为SSD算法中没有用到足够低层的特征（在SSD中，最低层的特征是VGG网络的conv4_3），而在作者看来足够低层的特征对于检测小物体是很有帮助的。 （d）FPN：这是本文要讲的网络，FPN主要解决的是物体检测中的多尺度问题，通过简单的网络连接改变，在基本不增加原有模型计算量的情况下，大幅度提升了小物体检测的性能。通过高层特征进行上采样和低层特征进行自顶向下的连接，而且每一层都会进行预测。 2....

一、传统的图像金字塔 最开始在深度学习方法流行之前，对于不同尺度的目标，大家普遍使用将原图构建出不同分辨率的图像金字塔，再对每层金字塔用固定输入分辨率的分类器在该层滑动来检测目标，以求在金字塔底部检测出小目标；或者只用一个原图，在原图上，用不同分辨率的分类器来检测目标，以求在比较小的窗口分类器中检测到小目标。经典的基于简单矩形特征(Haar)+级联Adaboost与Hog特征+SVM的DPM目标识别框架，均使用图像金字塔的方式处理多尺度目标，早期的CNN目标识别框架同样采用该方式，但对图像金字塔中的每一层分别进行CNN提取特征，耗时与内存消耗均无法满足需求。但该方式毫无疑问仍然是最优的。值得一提的是，其实目前大多数深度学习算法提交结果进行排名的时候，大多使用多尺度测试。同时类似于SNIP使用...

SoftNMS/DIoUNMS softnms参考： SoftNMS 可以看到，SoftNMS与传统NMS的区别在于对score分数调整的处理。如果是传统的NMS操作，那么当 B 中的 b_i 和 [Math] 的IoU值大于阈值 N_t ，那么就从 B 和 S 中去除该box；对于SoftNMS而言是先计算 [Math] 与 b_i 的IoU，然后IoU经过一个函数输出最后与 s_i 相乘最终得到box的分数。 其中 s_i 的score遵循IoU越大，分数越低的原则（IoU越大，越可能是背景），所以 s_i 定义如下： 考虑到上式是不连续的，并且当达到N_t的NMS阈值时会施加突然的惩罚， 如果惩罚函数是连续的，那将是理想的，否则它可能导致检测结果的排序列表的突然改变（集合D中的scor...

SNIPER的关键是减少了SNIP的计算量。SNIP借鉴了multiscale training的思想进行训练，multiscale training是用图像金字塔作为模型的输入，这种做法虽然能够提高模型效果，但是计算量的增加也非常明显，因为模型需要处理每个scale图像的每个像素，而SNIPER（Scale Normalization for Image Pyramids with Efficient Resampling）算法以适当的比例处理ground truth（称为chips）周围的上下文区域，在训练期间每个图像生成的chips的数量会根据场景复杂度而自适应地变化，由于SNIPER在采样后的低分辨率的chips上运行，故其可以在训练期间收益于Batch Normalization，...

简短总结 混合专家模型 (MoEs): 与稠密模型相比， 预训练速度更快 与具有相同参数数量的模型相比，具有更快的 推理速度 需要 大量显存，因为所有专家系统都需要加载到内存中 在 微调方面存在诸多挑战，但 近期的研究 表明，对混合专家模型进行 指令调优具有很大的潜力。 什么是混合专家模型？ 模型规模是提升模型性能的关键因素之一。在有限的计算资源预算下，用更少的训练步数训练一个更大的模型，往往比用更多的步数训练一个较小的模型效果更佳。 混合专家模型 (MoE) 的一个显著优势是它们能够在远少于稠密模型所需的计算资源下进行有效的预训练。这意味着在相同的计算预算条件下，您可以显著扩大模型或数据集的...

💡 引言 Trust Region Policy Optimization (TRPO) 是2015年的ICML会议上提出的一种强大的基于策略的强化学习算法。TRPO 解决了传统策略梯度方法中的一些关键问题，特别是训练不稳定和步长选择困难的问题。与传统策略梯度算法相比，TRPO 具有更高的稳健性和样本效率，能够在复杂环境中取得更好的性能。 优化基础 在深入了解 TRPO 之前，我们需要先简单回顾一些优化方法的基础知识。 梯度上升法 梯度上升法是一种迭代优化算法，用于寻找函数的局部最大值。 目标：找到使目标函数 [Math] 最大化的参数 [Math] ： [公式] 梯度上升迭代过程： 1. 在当前参数 [Math] 处计算梯度： [Math] 1. 更新参数： 梯度上升法的主要问题是学习率的...

概述 问题定义 广义的 Gaze Estimation 泛指与眼球、眼动、视线等相关的研究，因此有不少做 saliency 和 egocentric 的论文也以 gaze 为关键词。而本文介绍的 Gaze Estimation 主要以眼睛图像或人脸图像为处理对象，估算人的视线方向或注视点位置， 如下图所示。 gaze角度的表示一般使用一个3d向量作为表示，也可以转换为pitch 和yaw角度，具体可参考 Model Gaze模型一般使用回归模型，所以这里基本只介绍一些在gaze model中使用的小技巧 Rle Loss 实际问题