简介

生成树（spanning tree）

在图论中，无向图\(G=(V,E)\) 的生成树（spanning tree)是具有G的全部顶点，但边数最少的联通子图。假设G中一共有n个顶点，一颗生成树满足下列条件：
（1）n个顶点；
（2）n-1条边；
（3）n个顶点联通；
（4）一个图的生成树可能有多个。最小生成树（minimum spanning tree， MST）/最小生成森林：联通加权无向图中边缘权重加和最小的生成树。给定无向图 \(G=(V,E)\)，\((u,v)\) 代表顶点\(u\)与顶点\(v\)的边，\(w(u,v)\) 代表此边的权重，若存在生成树T使得：

\[ w(T) = \sum_{(u,v)\in T}w(w,v) \]

最小，则 \(T\) 为\(G\) 的最小生成树。对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。最小生成树除了继承生成树的性质之外，还存在下面两个特点：

当图的每一条边的权值都相同时，该图的所有生成树都是最小生成树；
如果图的每一条边的权值都互不相同，那么最小生成树将只有一个。
最小生成树示例：

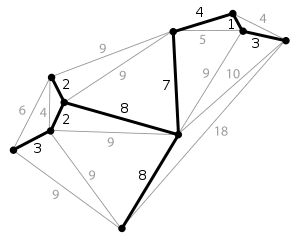
最小生成树MST的实际应用

构建成本最小的连接网络：电网，计算机网络、交通网络、供应链网络；
最小生成树聚类：考虑数据集D，计算两点之间的距离当作边缘权重（一般采用欧式距离）。最小生成树聚类思想为，首先通过Prim等算法对数据集生成最小生成树，然后根据给定的阈值对最小生成树的边权重进行扫描，当边缘权重大于设定的阈值时，将对应的边切断。对所有数据执行上述操作后，剩下的还相互连接的部分即为相同的类或簇。
反洗钱：核心交易网络发现+核心交易路线分

Prim算法介绍

Prim's Algorithm也翻译做普里姆算法，是1930年捷克数学家算法沃伊捷赫·亚尔尼克发现；并在1957年由美国计算机科学家罗伯特·普里姆独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

Prim算法的思想

从任意一个顶点开始，每次选择与当前顶点最近的一个顶点，并将两点之间的边加入到树中。算法描述如下：

输入：加权无向图\(G\)，顶点集合为\(V\)，边集合为\(E\)；

初始化: \(V_{new}=s\)，\(s\) 为集合\(V\) 中选择的任意起始点，\(E_{new}=\{\}\)；

重复下列操作，直到 \(V_{new}=V\):
3.1 在集合\(E\) 中选取权值最小的边\((u, v)\) ，其中\(u\) 为集合\(V_{new}\)中的元素，
而\(v\) 则是\(V\) 中没有加入\(V_{new}\) 的顶点（如果存在有多条满足前述条件即
具有相同权值的边，则可任意选取其中之一）；
3.2 将\(v\) 加入集合\(V_{new}\)中，将\((u, v)\) 加入集合\(E_{new}\) 中；

输出：使用集合\(V_{new}\)和\(E_{new}\)来描述所得到的最小生成树。

图例描述

输入：

说明：此为原始加权无向连通图，每条边的数字代表其权重；

第1步：假设初始化s为顶点D，顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示

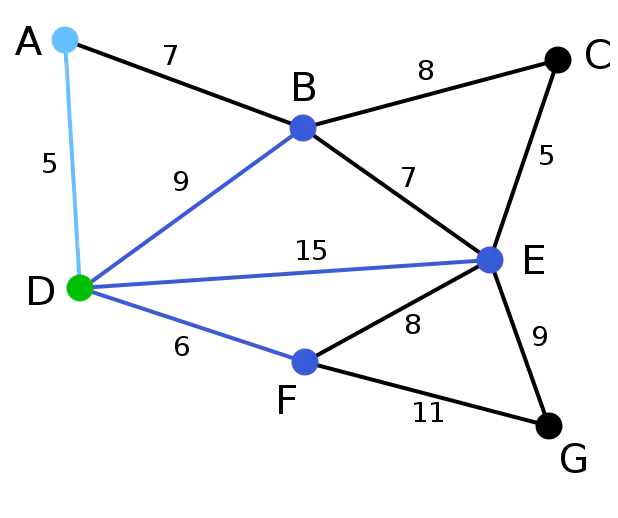
第2步：下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。

第3步：算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。

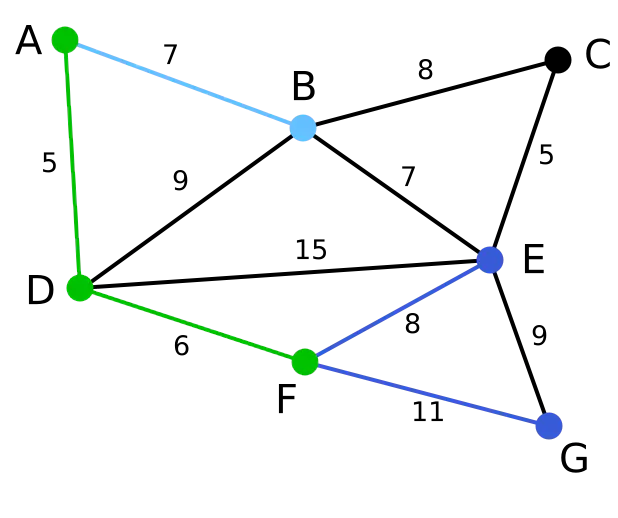
第4步：在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。

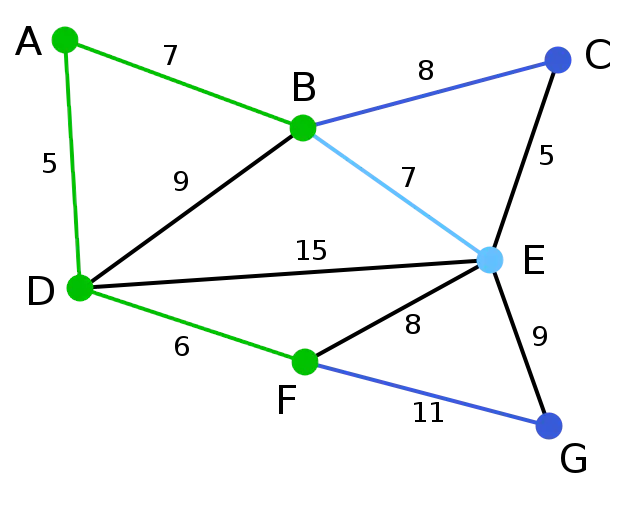
第5步：这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。

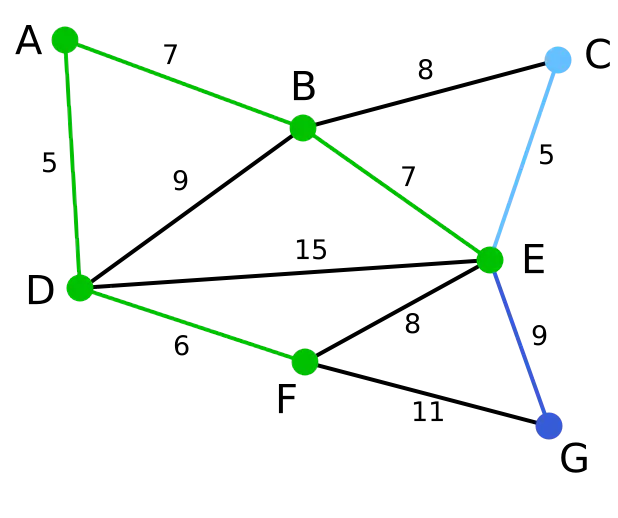
第6步：顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。

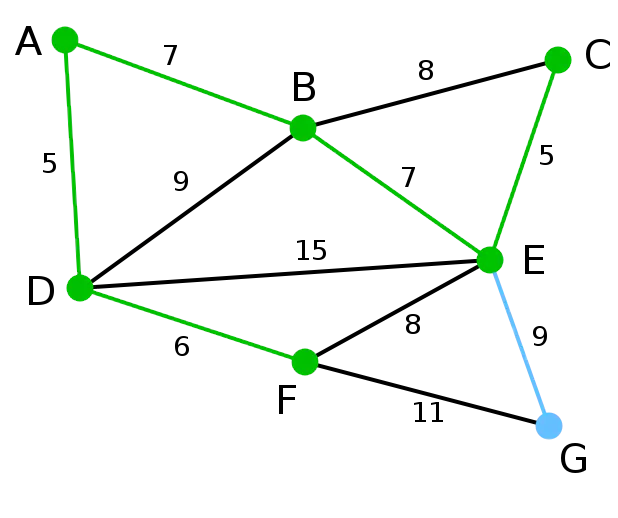
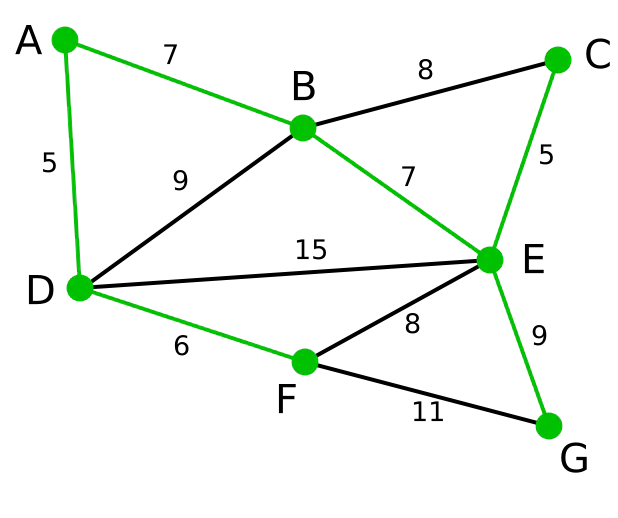
输出：所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。

算法代码

import random
import time


def random_matrix_genetor(vex_num=10):
    '''
    随机图顶点矩阵生成器
    输入：顶点个数，即矩阵维数
    '''
    data_matrix = []
    for i in range(vex_num):
        one_list = []
        for j in range(vex_num):
            if i == j:
                one_list.append(0)
            else:
                one_list.append(random.randint(1, 100))
        data_matrix.append(one_list)
    return data_matrix


def prim(data_matrix):
    '''
    prim 算法
    data_matrix: List[List[int]] i->j:weight
    '''
    vex_num = len(data_matrix)
    prims = [0] * vex_num
    weights = [0] * vex_num
    flag_list = [False] * vex_num
    node = 0    # 初始化节点
    flag_list[node] = True
    for i in range(vex_num):
        weights[i] = data_matrix[node][i]

    for _ in range(vex_num - 1):
        min_value = float('inf')
        for j in range(vex_num):
            if weights[j] != float('inf') and weights[j] < min_value and not flag_list[j]:
                min_value = weights[j]
                node = j
        if node == 0:
            return
        flag_list[node] = True
        for m in range(vex_num):
            if weights[m] > data_matrix[node][m] and not flag_list[m]:
                weights[m] = data_matrix[node][m]
                prims[m] = node
    return weights, prims


def main_test_func(vex_num=10):
    '''
    主测试函数
    '''
    start_time = time.time()
    data_matrix = random_matrix_genetor(vex_num)
    weights, prims = prim(data_matrix)
    print(weights)
    print(prims)
    end_time = time.time()
    return end_time - start_time


if __name__ == '__main__':
    time_list = []
    print('----------------------------10顶点测试-------------------------------------')
    time10 = main_test_func(10)
    time_list.append(time10)

    print('----------------------------50顶点测试-------------------------------------')
    time50 = main_test_func(50)
    time_list.append(time50)

    print('----------------------------100顶点测试-------------------------------------')
    time100 = main_test_func(100)
    time_list.append(time100)

    print('---------------------------------时间消耗对比--------------------------------')
    for one_time in time_list:
        print(one_time)

输出：

----------------------------10顶点测试-------------------------------------
[0, 27, 11, 7, 17, 2, 1, 13, 16, 2]
[0, 7, 6, 0, 9, 0, 7, 5, 5, 2]
----------------------------50顶点测试-------------------------------------
[0, 4, 4, 6, 5, 1, 5, 4, 1, 4, 4, 5, 2, 5, 1, 2, 6, 4, 1, 1, 3, 1, 3, 4, 4, 1, 4, 6, 2, 4, 4, 3, 2, 6, 8, 1, 1, 2, 4, 2, 4, 2, 4, 1, 2, 1, 3, 6, 4, 5]
[0, 48, 48, 32, 44, 0, 0, 31, 5, 32, 7, 31, 49, 12, 13, 46, 8, 22, 7, 5, 32, 49, 28, 15, 17, 45, 23, 40, 8, 37, 42, 22, 17, 46, 10, 7, 10, 28, 28, 23, 2, 33, 23, 38, 25, 18, 32, 24, 36, 4]
----------------------------100顶点测试-------------------------------------
[0, 1, 3, 4, 2, 2, 1, 1, 1, 2, 1, 1, 1, 3, 1, 4, 1, 3, 2, 1, 2, 1, 1, 2, 5, 3, 2, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 2, 2, 3, 2, 1, 1, 2, 1, 2, 2, 2, 1, 2, 3, 2, 1, 1, 3, 1, 1, 1, 2, 1, 1, 1, 1, 2, 1, 4, 2, 3, 2, 6, 3, 1, 1, 1, 1, 1, 3, 1, 4, 3, 2, 2, 2, 2, 4, 2, 2, 1, 1, 2, 1]
[0, 55, 67, 63, 19, 10, 43, 34, 42, 70, 68, 8, 42, 70, 7, 37, 24, 58, 84, 68, 5, 73, 32, 22, 0, 53, 24, 23, 87, 16, 88, 84, 35, 68, 12, 84, 22, 36, 65, 80, 58, 16, 97, 97, 60, 73, 77, 24, 34, 40, 11, 49, 10, 9, 44, 58, 10, 52, 5, 70, 96, 8, 2, 6, 97, 37, 14, 40, 9, 82, 6, 23, 35, 23, 3, 89, 48, 24, 50, 37, 22, 27, 58, 72, 69, 84, 63, 92, 97, 82, 66, 84, 4, 79, 22, 22, 17, 41, 90, 11]
---------------------------------时间消耗对比--------------------------------
0.0002970695495605469
0.006517887115478516
0.016569852828979492

Kruskal算法介绍

算法思想

Kruskal是另一个计算最小生成树的算法，由Joseph Kruskal在1956年发表，属于贪婪算法。
算法原理：将每个顶点放入其自身的数据集中，然后按照权重的升序来选择边。当选择每条边时，判断定义边的顶点是否在不同的数据集中。如果是，将此边插入最小生成树的集合中，将集合中包含每个顶点的联合体取出。算法描述如下：

新建图G，G中拥有原图中相同的节点，但不包含边；

将原图中所有的边按权值从小到大排讯；

从权值最小的边开始，如果这条边连接的两个节点在G中不在同一个分量，
则添加这条边到图G中；

重复3，直到图G中所有的节点在同一个联通分量中

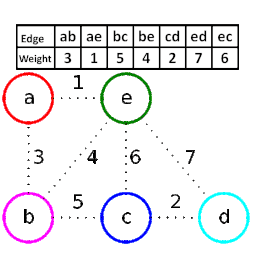
图例描述

Kruskal算法的演示如下：
假设有一张图G，包含若干点和边。

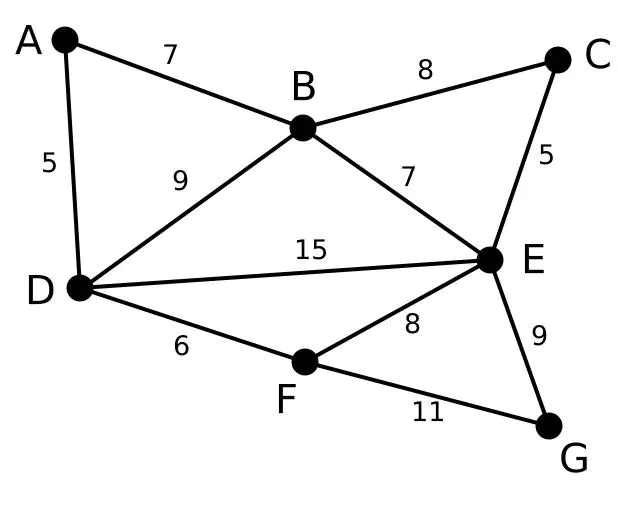
第1步：将所有的边的长度排序，用排序的结果作为选择边的依据。资源排序，对局部最优的资源进行选择，排序完成后，率先选择了边AD。

第2步：在剩下的边中寻找，找到了CE。这里边的权重也是5

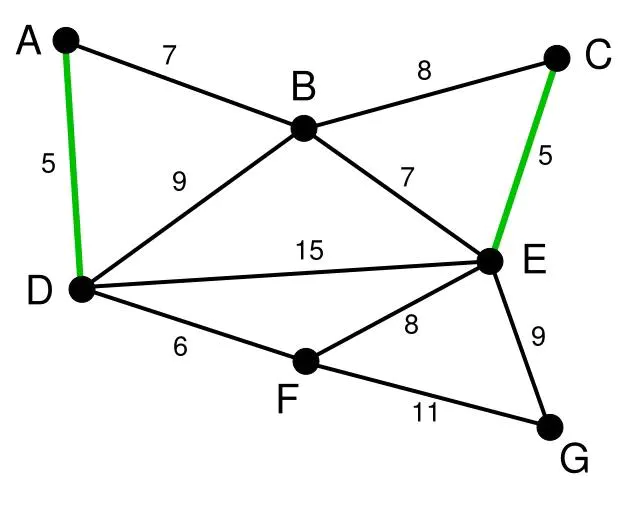
第3步：依次类推找到了DF，AB，BE。

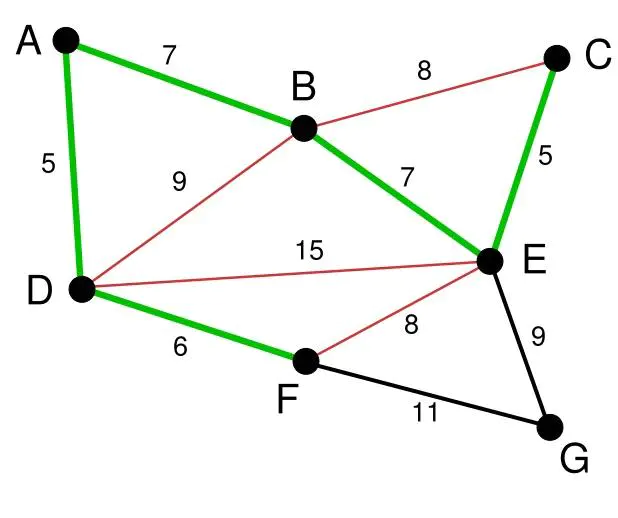
第4步：下面继续选择， BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了（对于BC可以通过CE,EB来连接，类似的EF可以通过EB,BA,AD,DF来接连）。所以不需要选择他们。类似的BD也已经连通了（这里上图的连通线用红色表示了）。最后就剩下EG和FG了。当然我们选择了EG。（等判断是否联通）

代码实现

node = dict()
rank = dict()

def make_set(point):
    node[point] = point
    rank[point] = 0

def find(point):
    if node[point] != point:
        node[point] = find(node[point])
    return node[point]

def merge(point1, point2):
    root1 = find(point1)
    root2 = find(point2)
    if root1 != root2:
        if rank[root1] > rank[root2]:
            node[root2] = root1
        else:
            node[root1] = root2
            if rank[root1] == rank[root2] : rank[root2] += 1

def Kruskal(graph):
    for vertice in graph['vertices']:
        make_set(vertice)

    mst = set()

    edges = list(graph['edges'])
    edges.sort()
    for edge in edges:
        weight, v1, v2 = edge
        if find(v1) != find(v2):
            merge(v1 , v2)
            mst.add(edge)
    return mst

graph = {
    'vertices': ['A', 'B', 'C', 'D','E'],
    'edges': set([
        (1, 'A', 'B'),
        (5, 'A', 'C'),
        (3, 'A', 'D'),
        (4, 'B', 'C'),
        (2, 'B', 'D'),
        (1, 'C', 'D'),
        (8, 'B', 'E'),
        (3, 'A', 'E'),
        ])
    }
print(Kruskal(graph))

输出：

{(1, 'C', 'D'), (1, 'A', 'B'), (3, 'A', 'E'), (2, 'B', 'D')}

Reference

图遍历算法之最小生成树Prim算法与 Kruskal算法