为什么要进行相机标定？

先说结论：建立相机成像几何模型并矫正透镜畸变。

建立相机成像几何模型：计算机视觉的首要任务就是要通过拍摄到的图像信息获取到物体在真实三维世界里相对应的信息，于是，建立物体从三维世界映射到相机成像平面这一过程中的几何模型就显得尤为重要，而这一过程最关键的部分就是要得到相机的内参和外参（后文有具体解释）。

矫正透镜畸变：我们最开始接触到的成像方面的知识应该是有关小孔成像的，但是由于这种成像方式只有小孔部分能透过光线就会导致物体的成像亮度很低，于是聪明的人类发明了透镜。虽然亮度问题解决了，但是新的问题又来了：由于透镜的制造工艺，会使成像产生多种形式的畸变，于是为了去除畸变（使成像后的图像与真实世界的景象保持一致），人们计算并利用畸变系数来矫正这种像差。（虽然理论上可以设计出不产生畸变的透镜，但其制造工艺相对于球面透镜会复杂很多，so相对于复杂且高成本的制造工艺，人们更喜欢用脑子来解决……）

相机标定的原理

前面已经说过，相机标定的目的之一是为了建立物体从三维世界到成像平面上各坐标点的对应关系，所以首先我们需要定义这样几个坐标系来为整个过程做好铺垫：

世界坐标系(world coordinate system)：用户定义的三维世界的坐标系，为了描述目标物在真实世界里的位置而被引入。单位为m。

相机坐标系(camera coordinate system)：在相机上建立的坐标系，为了从相机的角度描述物体位置而定义，作为沟通世界坐标系和图像/像素坐标系的中间一环。单位为m。

图像坐标系(image coordinate system)：为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入，方便进一步得到像素坐标系下的坐标。单位为m。

像素坐标系(pixel coordinate system)：为了描述物体成像后的像点在数字图像上（相片）的坐标而引入，是我们真正从相机内读取到的信息所在的坐标系。单位为个（像素数目）。

下面的图可以很好地表达这四个坐标系之间的关系：

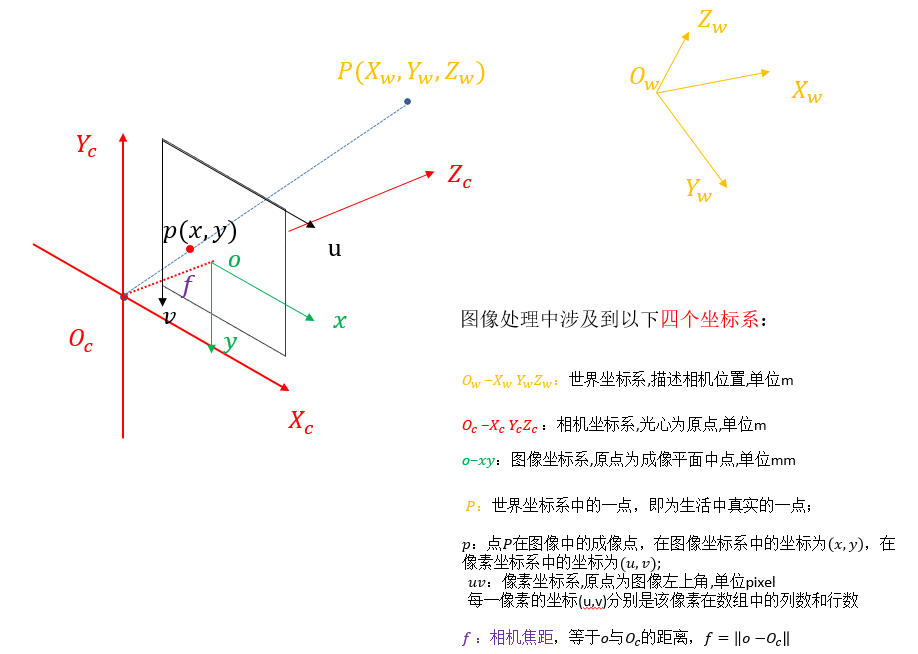
构建世界坐标系只是为了更好的描述相机的位置在哪里，在双目视觉中一般将世界坐标系原点定在左相机或者右相机或者二者X轴方向的中点。

接下来的重点，就是关于这几个坐标系的转换。也就是说，一个现实中的物体是如何在图像中成像的。

世界坐标系与相机坐标系

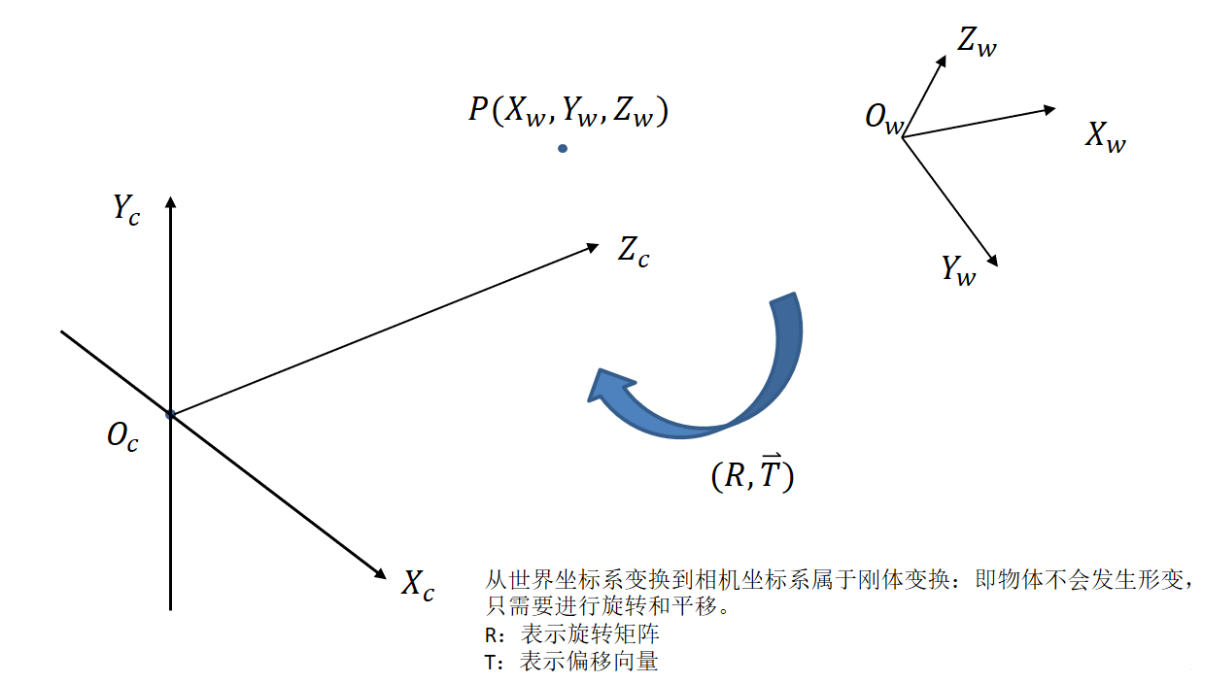
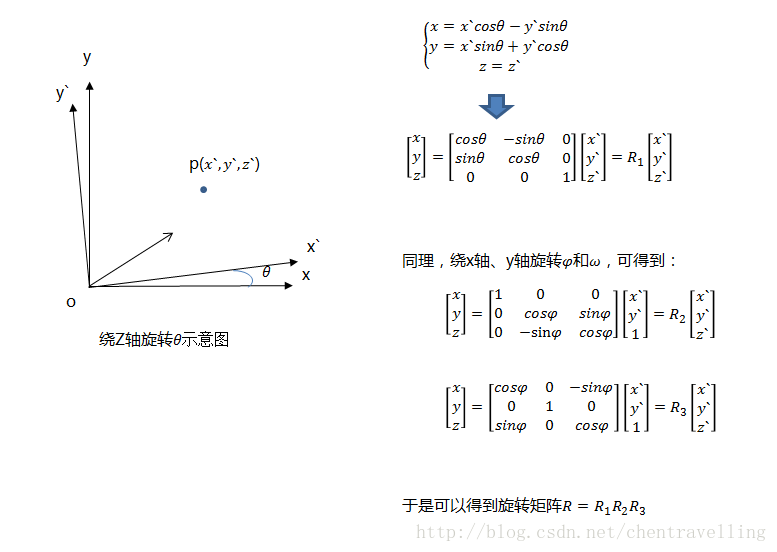
于是，从世界坐标系到相机坐标系，涉及到旋转和平移（其实所有的运动也可以用旋转矩阵和平移向量来描述）。绕着不同的坐标轴旋转不同的角度，得到相应的旋转矩阵，如下图所示：

我们将其变换矩阵由一个旋转矩阵和平移向量组合成的齐次坐标矩阵来表示：

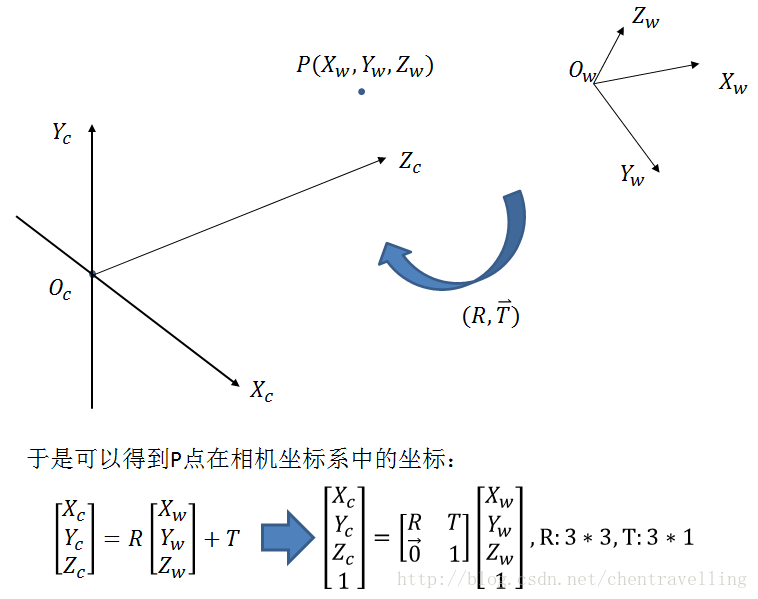
其中，R为旋转矩阵，t为平移向量，因为假定在世界坐标系中物点所在平面过世界坐标系原点且与Zw轴垂直（也即棋盘平面与Xw-Yw平面重合，目的在于方便后续计算），所以\(Z_w=0\)，可直接转换成式1的形式。其中变换矩阵

即为前文提到的外参矩阵，之所称之为外参矩阵可以理解为只与相机外部参数有关，且外参矩阵随刚体位置的变化而变化。

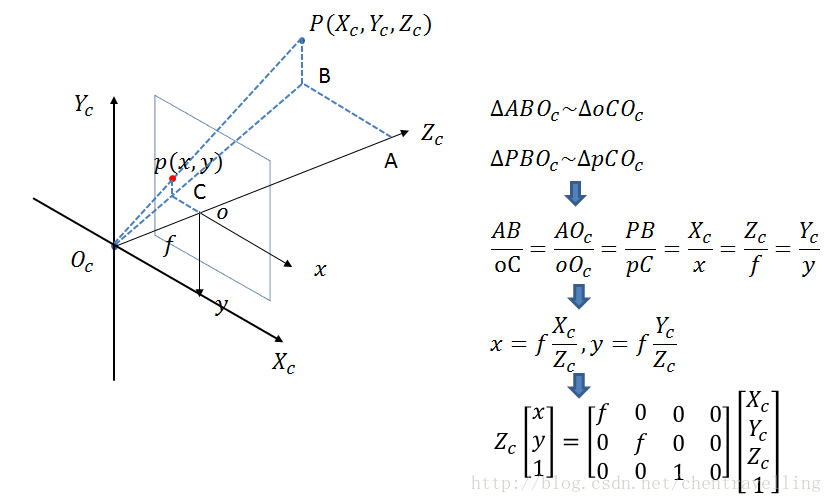
从相机坐标系到理想图像坐标系（不考虑畸变）：

从相机坐标系到图像坐标系，属于透视投影关系，从3D转换到2D。

从理想图像坐标系到实际图像坐标系（考虑畸变）：

透镜的畸变主要分为径向畸变和切向畸变（还有薄透镜畸变等等，但都没有径向和切向畸变影响显著，所以我们在这里只考虑径向和切向畸变）。

径向畸变

径向畸变是由于透镜形状的制造工艺导致。且越向透镜边缘移动径向畸变越严重。

实际情况中我们常用r=0处的泰勒级数展开的前几项来近似描述径向畸变。矫正径向畸变前后的坐标关系为：

\[ \left\{\begin{aligned}x_d&=&x(1+k_1r^2+k_2r^4+k_3r^6)\\y_d&=&y(1+k_1r^2+k_2r^4+k_3r^6)\end{aligned}\right. \]

\(x,y\) 是归一化的图像坐标，即坐标原点已经移动到主点，并且像素坐标除以焦距。\(k_1,k_2,k_3\)是径向畸变系数，\(r^2=x^2+y^2\)

切向畸变

切向畸变主要发生在相机sensor和镜头不平行的情况下；因为有夹角，所以光透过镜头传到图像传感器上时，成像位置发生了变化。

\[ \left\{\begin{aligned}x_d&=&x+[2p_1xy+p_2(r^2+2x^2)]\\y_d&=&y+[2p_2xy+p_1(r^2+2x^2)]\end{aligned}\right. \]

由此可知对于切向畸变，我们有2个畸变参数需要求解。

综上，我们一共需要5个畸变参数（k1、k2、k3、p1和p2 ）来描述透镜畸变。

从实际图像坐标系到像素坐标系

像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点，通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。所以这二者之间的转换如下：其中dx和dy表示每一列和每一行分别代表多少mm，即1pixel=dx mm

那么通过上面四个坐标系的转换就可以得到一个点从世界坐标系如何转换到像素坐标系(无畸变)的。

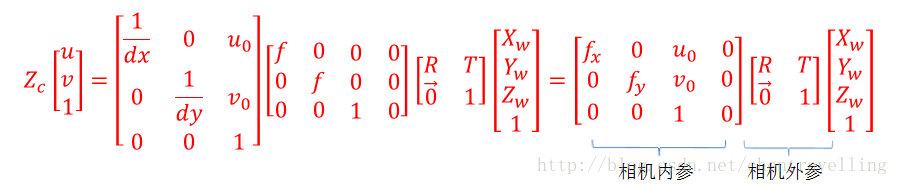
张正友标定算法

”张正友标定”是指张正友教授1998年提出的单平面棋盘格的摄像机标定方法。文中提出的方法介于传统标定法和自标定法之间，但克服了传统标定法需要的高精度标定物的缺点，而仅需使用一个打印出来的棋盘格就可以。同时也相对于自标定而言，提高了精度，便于操作。因此张氏标定法被广泛应用于计算机视觉方面。

计算内参和外参的初值

这里引入单应性的概念。在计算机视觉中的单应性被定义为从一个平面到另一个平面的投影映射关系。

计算单应性矩阵\(H\)

根据之前介绍的摄像机模型，设三维世界坐标的点为\(X=[X,Y,Z,1]^T\)，二维相机平面像素坐标为\(m=[u,v,1]^T\)，所以标定用的棋盘格平面到图像平面的单应性关系为：

\[ s_0m = K[R, T]X \]

其中\(s\) 为尺度因子，\(K\)为摄像机内参数，\(R\)为旋转矩阵，\(T\)为平移向量。令

\[ K=\left[ \begin{array}{ccc} \alpha & \gamma & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \end{array} \right] \]

注意，\(s\) 对于齐次坐标来说，不会改变齐次坐标值。张氏标定法中，将世界坐标系构建在棋盘格平面上，令棋盘格平面为Z=0的平面。则可得

\[ s\left[ \begin{array}{c} u \\ v \\ 1 \end{array} \right] = K\left[ \begin{array}{cccc} r_1 & r_2 & r_3 & t \end{array} \right] \left[ \begin{array}{c} X \\ Y \\ 0 \\ 1 \end{array} \right]=K \left[ \begin{array}{cccc} r_1 & r_2 & t \end{array} \right] \left[ \begin{array}{c} X \\ Y \\ 1 \end{array} \right] \]

我们把\(K[r_1, r_2, t]\) 叫做单应性矩阵\(H\)，即

\[ s \left[ \begin{array}{c} u \\ v \\ 1 \end{array} \right]= H \left[ \begin{array}{c} X \\ Y \\ 1 \end{array} \right]\\ H=[h_1\ h_2\ h_3] = \lambda K[r_1\ r_2\ t] \]

\(H\) 是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H。

计算内参数矩阵

由上式可得

\[ \lambda = \frac{1}{s} \\ r_1=\frac{1}{\lambda}K^{-1}h_1 \\ r_2=\frac{1}{\lambda}K^{-1}h_2 \]

由于旋转矩阵是个酉矩阵，\(r_1\)和\(r_2\)正交，可得

\[ r_1^Tr_2=0 \\ ||r_1||=||r_2||=1 \]

带入，得

\[ h_1^TK^{-T}K^{-1}h_2=0 \\ h_1^TK^{-T}K^{-1}h_1 = h_2^TK^{-T}K^{-1}h_2 \]

即每个单应性矩阵能提供两个方程，而内参数矩阵包含5个参数，要求解，至少需要3个单应性矩阵。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到三个不同的图片。为了方便计算，定义如下：

\[ B=K^{-T}K^{-1}= \left[ \begin{array}{ccc} B_{11} & B_{12} & B_{13} \\ B_{21} & B_{22} & B_{23} \\ B_{31} & B_{32} & B_{33} \end{array} \right]= \left[ \begin{array}{ccc} \frac{1}{\alpha^2} & -\frac{\gamma}{\alpha^2\beta} & \frac{v_0\gamma-u_0\beta}{\alpha^2\beta} \\ -\frac{\gamma}{\alpha^2\beta} & \frac{\gamma^2}{\alpha^2\beta^2}+\frac{1}{\beta^2} & -\frac{\gamma(v_0\gamma-u_0\beta)}{\alpha^2\beta^2}-\frac{v_0}{\beta^2} \\ \frac{v_0\gamma-u_0\beta}{\alpha^2\beta} & -\frac{\gamma(v_0\gamma-u_0\beta)}{\alpha^2\beta^2}-\frac{v_0}{\beta^2} & \frac{(v_0\gamma-u_0\beta)^2}{\alpha^2\beta^2}+\frac{v_0}{\beta^2}+1 \end{array} \right] \]

可以看到，B是一个对称阵，所以B的有效元素为六个，让这六个元素写成向量b，即

\[ b=\left[ \begin{array}{cccccc} B_{11} & B_{12} & B_{22} & B_{13} & B_{23} & B_{33} \end{array} \right]^T \]

可以推导得到

\[ h_i^TBh_j = v^T_{ij}b \\ v_{ij}=\left[ \begin{array}{cccccc} h_{i1}h_{j1} & h_{i1}h_{j2}+h_{i2}h_{j1} & h_{i2}h_{j2} & h_{i3}h_{j1}+h_{i1}h_{j3} & h_{i3}h_{j2}+h_{i2}h_{j3} & h_{i3}h_{j3} \end{array} \right]^T \]

利用约束条件可以得到：

\[ \left[ \begin{array}{c} v^T_{12} \\ (v_{11}-v_{22})^T \end{array} \right]b=0 \]

通过上式，我们至少需要三幅包含棋盘格的图像，可以计算得到B，然后通过cholesky分解，得到相机的内参数矩阵K。

计算外参数矩阵

由之前的推导，可得

\[ \lambda = \frac{1}{s}=\frac{1}{\|A^{-1}h_1\|}=\frac{1}{\|A^{-1}h_2\|} \\ r_1=\frac{1}{\lambda}K^{-1}h_1 \\ r_2=\frac{1}{\lambda}K^{-1}h_2 \\ r_3 = r_1 \times r_2 \\ t=\lambda K^{-1}h_3 \]

最大似然估计

上述的推导结果是基于理想情况下的解，但由于可能存在高斯噪声，所以使用最大似然估计进行优化。设我们采集了n副包含棋盘格的图像进行定标，每个图像里有棋盘格角点m个。令第i副图像上的角点Mj在上述计算得到的摄像机矩阵下图像上的投影点为：

\[ \hat{m}(K,R_i,t_i,M_{ij}) = K[R|t]M_{ij} \]

其中\(R_i\)和\(t_i\)是第i副图对应的旋转矩阵和平移向量，K是内参数矩阵。则角点\(m_{ij}\)的概率密度函数为：

\[ f(m_{ij})=\frac{1}{\sqrt{2\pi}}e^{\frac{-(\hat{m}(K,R_i,t_i,M_{ij})-m_{ij})^2}{\sigma^2}} \]

构造似然函数：

\[ L(A,R_i,t_i,M_{ij}) = \prod^{n,m}_{i=1,j=1}f(m_{ij})=\frac{1}{\sqrt{2\pi}}e^{\frac{-\sum^n_{i=1}\sum^m_{j=1}(\hat{m}(K,R_i,t_i,M_{ij})-m_{ij})^2}{\sigma^2}} \]

让L取得最大值，即让下面式子最小。这里使用的是多参数非线性系统优化问题的Levenberg-Marquardt算法进行迭代求最优解。

\[ \sum^n_{i=1}\sum^m_{j=1} \| \hat{m}(K,R_i,t_i,M_{ij})-m_{ij} \|^2 \]

径向畸变估计

张氏标定法只关注了影响最大的径向畸变。则数学表达式为：

\[ \hat u = u + (u-u_0)[k_1(x^2+y^2)+k_2(x^2+y^2)^2] \\ \hat v = v + (v-v_0)[k_1(x^2+y^2)+k_2(x^2+y^2)^2] \]

其中，\((u,v)\) 是理想无畸变的像素坐标， \((û ,v̂ )\)是实际畸变后的像素坐标。\((u_0,v_0)\)代表主点，\((x,y)\)是理想无畸变的连续图像坐标， \((x̂ ,ŷ )\)是实际畸变后的连续图像坐标。\(k_1\)和\(k_2\)为前两阶的畸变参数。

\[ \hat u = u_0 + \alpha \hat x + \gamma \hat y \\ \hat v = v_0 + \beta \hat y \]

化作矩阵形式：

\[ \left[ \begin{array}{cc} (u-u_0)(x^2+y^2) & (u-u_0)(x^2+y^2)^2 \\ (v-v_0)(x^2+y^2) & (v-v_0)(x^2+y^2)^2 \end{array} \right] \left[ \begin{array}{c} k_1 \\ k_2 \end{array} \right]= \left[ \begin{array}{c} \hat u -u \\ \hat v -v \end{array} \right] \]

记做：

\[ Dk=d \]

可得：

\[ k=[k_1\ k_2]^T = (D^TD)^{-1}D^Td \]

计算得到畸变系数k。

使用最大似然的思想优化得到的结果，即像上一步一样，LM法计算下列函数值最小的参数值：