前言
双目立体视觉是基于视差原理,由多幅图像获取物体三维几何信息的方法。在机器视觉系统中,双目视觉一般由双摄像机从不同角度同时获取周围景物的两幅数字图像,或有由单摄像机在不同时刻从不同角度获取周围景物的两幅数字图像,并基于视差原理即可恢复出物体三维几何信息,重建周围景物的三维形状与位置。
双目视觉有的时候我们也会把它称为体视,是人类利用双眼获取环境三维信息的主要途径。从目前来看,随着机器视觉理论的发展,双目立体视觉在机器视觉研究中发回来看了越来越重要的作用。本篇帖子主要研究了双目视觉的数学原理。
为什么非得用双目相机才能得到深度?
说到这里,有些读者会问啦:为什么非得用双目相机才能得到深度?我闭上一只眼只用一只眼来观察,也能知道哪个物体离我近哪个离我远啊!是不是说明单目相机也可以获得深度?
在此解答一下:首先,确实人通过一只眼也可以获得一定的深度信息,不过这背后其实有一些容易忽略的因素在起作用:一是因为人本身对所处的世界是非常了解的(先验知识),因而对日常物品的大小是有一个基本预判的(从小到大多年的视觉训练),根据近大远小的常识确实可以推断出图像中什么离我们远什么离我们近;二是人在单眼观察物体的时候其实人眼是晃动的,相当于一个移动的单目相机,这类似于运动恢复结构(Structure from Motion, SfM)的原理,移动的单目相机通过比较多帧差异确实可以得到深度信息。
双目立体视觉的数学原理
双目立体视觉是基于视差,由三角法原理进行三维信息的获取,即由两个摄像机的图像平面和北侧物体之间构成一个三角形。已知两个摄像机之间的位置关系,便可以获得两摄像机公共视场内物体的三维尺寸及空间物体特征点的三维坐标。所以,双目视觉系统一般由两个摄像机构成。
双目立体视觉三维测量原理
理想双目相机成像模型
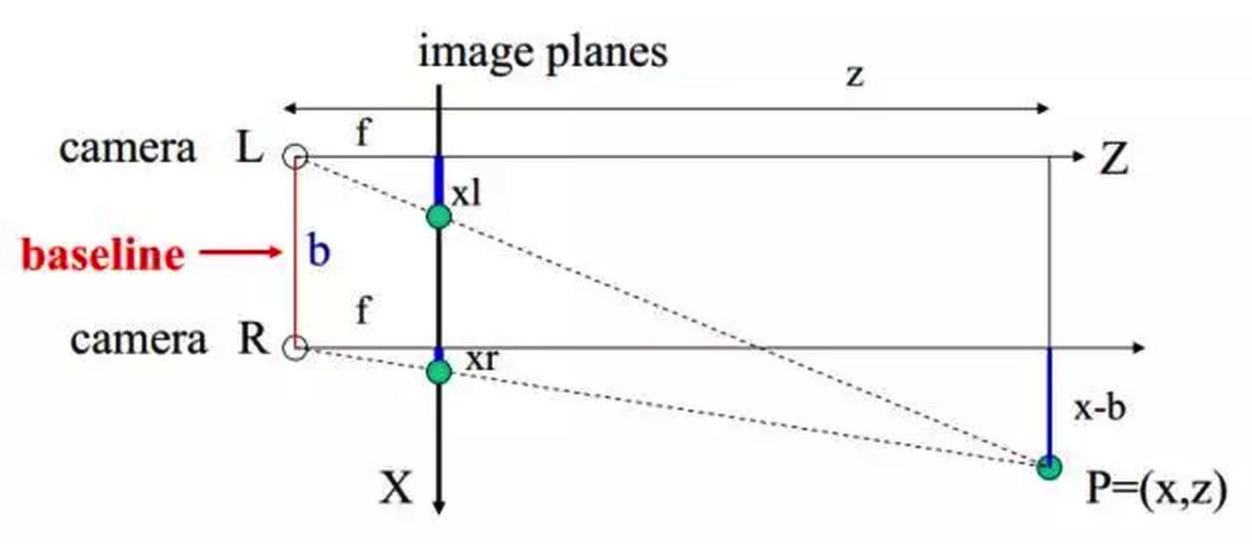
上图所示为简单的平视双目立体成像原理图,两摄像机的投影中心连线的距离,即基线距离\(b\) 。两摄像机在同一时刻观看时空物体的同一特征点P,分别在“左眼”和“右眼”上获取了点P的图像,他们的坐标分别为\(P_L=(X_L,Y_R)\);\(P_R=(X_R,Y_R)\)。将定两摄像机的图像在同一平面上,则特征点\(P\) 的图像坐标的Y坐标一定是相同的,即\(Y_L=Y_R=Y\)。由三角几何关系可以得到如下关系式:
则视差为:\(d=x_l-x_r\).由此可以计算出特征点P在摄像机坐标系下的三维坐标:
因此,左摄像机像面上的任意一点只要能在右摄像机像面上找到对应的匹配点,就完全可以确定该点的三维坐标。这种方法是点对点的运算,像平面上所有点只要存在相应的匹配点,就可以参与上述运算,从而获取对应的三维坐标。
双目立体视觉数学模型

在分析了最简单的平视双目立体视觉的三维测量原理基础上,现在我们就有能力来考虑一般情况。如上图所示,设左摄像机\(O-xyz\)位于世界坐标系原点,且没有发生旋转,图像坐标系为\(O_l-X_1Y_1\),有效焦距为fl;右摄像机坐标系为\(O_r-xyz\),图像坐标系为\(O_r-X_rY_r\),有效焦距为fr。那么根据摄像机的投射模型我们就能得到如下关系式:
因为\(O-xyz\)坐标系与\(O_r-x_ry_rz_r\)坐标系之间的位置关系可通过空间转换矩阵\(M_{lr}\)表示为:
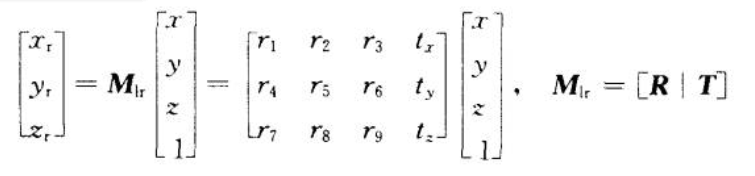
同理,对于\(O-xyz\)坐标系中的空间点,两个摄像机面点之间的对应关系可以表示为
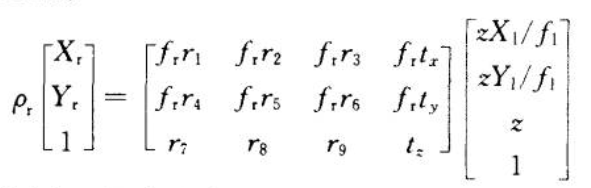
于是,空间点三维坐标可以表示为

因此,只要我们通过计算机标定技术获得左右计算机内参数/焦距fr,fl和空间点在左右摄像机中的图像坐标,就能够重构出被测点的三维空间坐标。