RL基础概念

Feb 19, 2025
1 views
Reinforcement Learning
# Reinforcement Learning

基础概念

Grid-Word Example

image

  • 环境描述：网格世界是一个直观的二维环境，包含：
  • 任务目标：

什么是强化学习：依据策略执行动作-感知状态-得到奖励

所谓强化学习(Reinforcement Learning，简称RL)，是指基于智能体在复杂、不确定的环境中最大化它能获得的奖励，从而达到自主决策的目的。

a computational approach to learning whereby an agent tries to maximize the total amount of reward it receives while interacting with a complex and uncertain environment

经典的强化学习模型可以总结为下图的形式（你可以理解为任何强化学习都包含这几个基本部分：智能体、行为、环境、状态、奖励）：

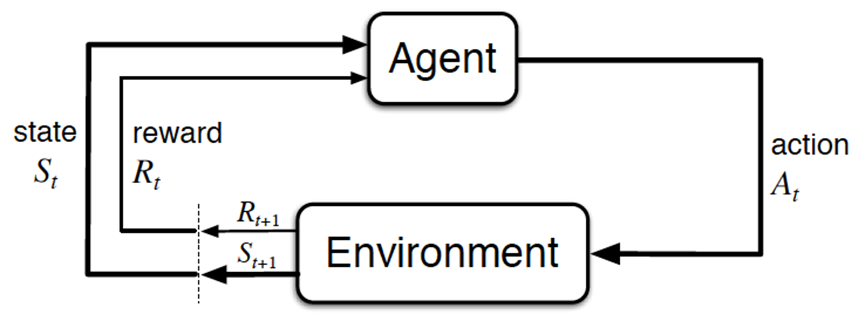
image

一般的文章在介绍这些概念时很容易一带而过，这里我把每个概念都逐一解释下

  • Agent：一般译为智能体，就是我们要训练的模型，比如在Grid-World的小机器人就是Agent
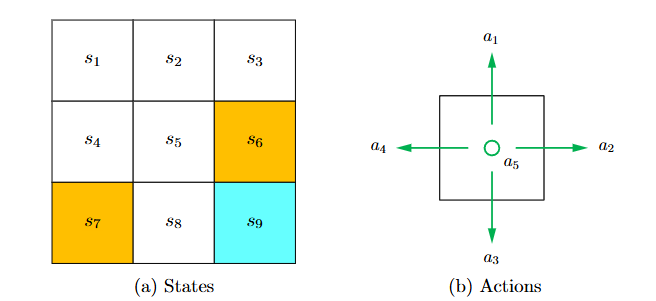
  • 状态（State）：状态描述了Agent 在环境中的位置。Grid-World示例：
  • 动作（Action）
  • 环境（Environment）：是提供reward的某个对象，它可以是Grid-world中的网格，也可以是自动驾驶中的人类驾驶员，甚至可以是某些游戏AI里的游戏规则
  • 奖励（reward）：简记为\(r\)，这个奖励可以类比为在明确目标的情况下，接近目标意味着做得好则奖励，远离目标意味着做的不好则惩，最终达到收益/奖励最大化，奖励是强化学习的核心
    image

总的而言，Agent依据策略决策从而执行动作action，然后通过感知环境Environment从而获取环境的状态state，进而，最后得到奖励reward(以便下次再到相同状态时能采取更优的动作)，然后再继续按此流程“依据策略执行动作-感知状态--得到奖励”循环进行。

状态转移

状态转移是Agent 执行某个动作后，从一个状态转移到另一个状态的过程。

状态转移可以是确定性的，也可以是随机性的。

网格世界示例

  • 确定性转移：代理在状态 \(s_1\) 执行动作 \(a_2\)（向右移动），则状态转移为：
    \(s_1 \xrightarrow{a_2} s_2\)
  • 随机性转移：如果环境中存在随机因素（如风力），代理可能偏离预期路径。例如：
    在状态 \(s_1\) 执行动作 \(a_2\) 时，有一定概率被吹到 \(s_5\) .

数学描述

状态转移通过条件概率表示：

$$
p(s'|s, a)

$$

表示Agent在状态 \(s\) 执行动作 \(a\) 后转移到状态 \(s'\) 的概率。

策略（Policy）

策略是代理在每个状态下选择动作的规则，描述为条件概率：

\[ \pi(a|s) \]

表示代理在状态 \(s\) 下选择动作 \(a\) 的概率。

类型

  • 确定性策略：
  • 随机性策略：
    表示方法：策略可以用表格表示，每个单元格表示在某状态下选择某动作的概率， 如下表所示

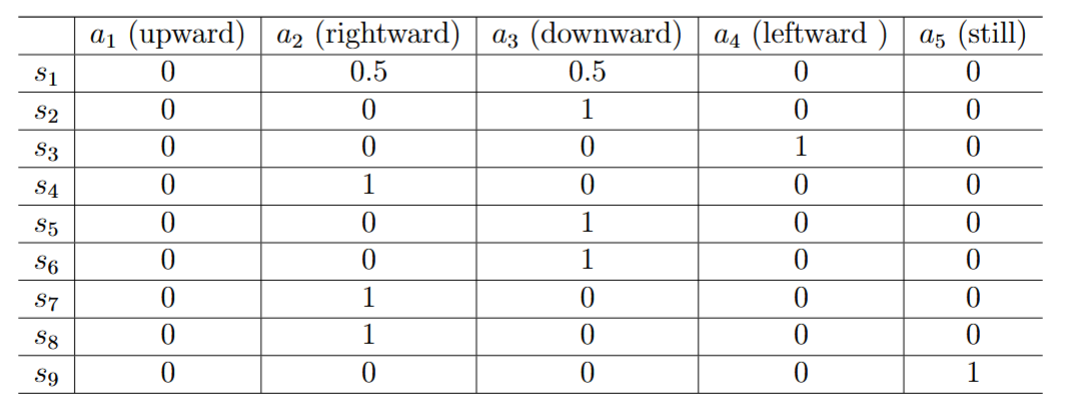
image

奖励（Reward）

奖励是Agent执行动作后从环境获得的反馈，用于引导代理的行为。并且奖励是状态和动作的函数：\(r(s, a)\)。

网格世界示例中奖励设计如下：

  • 出界：\(r_{\text{boundary}} = -1\)
  • 进入禁区：\(r_{\text{forbidden}} = -1\)
  • 到达目标：\(r_{\text{target}} = +1\)
  • 其他情况：\(r_{\text{other}} = 0\)

奖励的重要性

  • 奖励不仅影响即时决策，还决定Agent的长期策略。
  • 奖励设计需谨慎，特别是复杂任务中，需要深刻理解问题。
    同样， 奖励也可以表示成表格的形式：

image

轨迹、回报与折扣因子

轨迹（Trajectory）

轨迹是状态-动作-奖励的序列，例如：

$$

s_1 \xrightarrow{a_2, r=0} s_2 \xrightarrow{a_3, r=0} s_5 \xrightarrow{a_3, r=0} s_8 \xrightarrow{a_2, r=+1} s_9

$$

回报（Return）

回报是轨迹中所有奖励的总和，用于评估策略优劣：

\[ G = \sum_{t=0}^{T} r_t \]

对于无限长的轨迹，引入折扣因子 \(\gamma \in (0, 1)\) 计算折扣回报：

\[ G = \sum_{t=0}^{\infty} \gamma^t r_t \]

折扣因子的作用

\(\gamma\) 越接近0，Agent越关注近期奖励；\(\gamma\) 越接近1，代理越关注长期奖励。

在具体介绍折扣因子作用前，首先介绍一下Episode的概念：

当遵循策略与环境交互时，Agent可能会在某些终止状态状态停止。由此产生的轨迹称为 episode （或者叫 trial）。

通常假设 episode 是个有限的轨迹。包含episode的任务称为 epsodic task。但是，某些任务可能没有终止状态，这意味着与环境交互的过程永远不会结束。此类任务称为 continuing tasks。

对于终止状态可以有两种处理方式：

  • ** 第一种方法：将终止状态视为特殊状态（吸收状态）**
  • 第二种方法：将终止状态视为普通状态
    第二种方法带来一个问题：如果代理在目标状态 \(s_9\) 停留时持续获得正奖励（例如 \(r = 1\)），且轨迹是无限长的，那么总回报（Return）会趋于无穷大，因为奖励会不断累积。

解决方法：为了避免这种发散问题，需要引入折扣因子（Discount Rate，\(\gamma\)）。折扣因子满足 \(0 < \gamma < 1\)，用来逐步减少远期奖励的权重，使得总回报收敛到一个有限值。折扣回报公式为：

当 \(\gamma\) 较小时，Agent更关注短期奖励；当 \(\gamma\) 接近1时，Agent更关注长期奖励。

马尔可夫决策过程（MDP）

MDP（Markov decision processes）是用于描述随机动态系统的通用框架，广泛应用于强化学习。它提供了一种形式化的方法来定义状态、动作、奖励和状态转移等核心概念。

MDP的关键组成部分

集合（Sets）

MDP由以下三个基本集合构成：

  1. 状态空间（State Space, \(S\)）：所有可能状态的集合，表示为 \(S\)
  2. 动作空间（Action Space, \(A(s)\)）：每个状态下可执行动作的集合，表示为 \(A(s)\)，其中 \(s \in S\)
  3. 奖励集合（Reward Set, \(R(s, a)\)）：每个状态-动作对（\(s, a\)）对应的奖励集合，表示为 \(R(s, a)\)

模型（Model）

MDP通过以下两个概率分布描述状态转移和奖励生成的动态过程：

  1. 状态转移概率（State Transition Probability）：在状态 \(s\) 执行动作 \(a\) 后转移到下一状态 \(s'\) 的概率，表示为 \(p(s'|s, a)\)， 其中
  2. 奖励概率（Reward Probability）：在状态 \(s\) 执行动作 \(a\) 后获得奖励 \(r\) 的概率，表示为 \(p(r|s, a)\)

策略（Policy）

  • 定义：策略定义了代理在每个状态下选择动作的概率分布，表示为 [\pi(a|s)]。
  • 性质：
  • 示例：在网格世界中，代理在 s_1 的策略可能是：

马尔可夫性质（Markov Property）

  • 定义：马尔可夫性质指的是随机过程的“无记忆性”，即下一状态或奖励仅依赖当前状态和动作，与过去的状态和动作无关。
  • 数学描述：
    $$
    p(s_{t+1}|s_t, a_t, s_{t-1}, a_{t-1}, ..., s_0, a_0) = p(s_{t+1}|s_t, a_t)\
    p(r_{t+1}|s_t, a_t, s_{t-1}, a_{t-1}, ..., s_0, a_0) = p(r_{t+1}|s_t, a_t)
    $$

其中，\(t\) 表示当前时间步，\(t+1\) 表示下一时间步。

  • 意义：

MDP与MP的关系

什么是马尔可夫过程（Markov Process, MP）？

  • 定义：
  • 特性：
  • 离散时间马尔可夫链（Markov Chain）：

MDP与MP的区别