💡 ****

原本随机采样的DDPM模型中，也隐含了一个确定性的采样过程DDIM，它的连续极限也是一个ODE。

细想上述过程，可以发现不管是“DDPM→DDIM”还是“SDE→ODE”，都是从随机采样模型过渡到确定性模型，而如果我们一开始的目标就是ODE，那么该过程未免显得有点“迂回”了。在本文中，笔者尝试给出ODE扩散模型的直接推导，并揭示了它与雅可比行列式、热传导方程等内容的联系。

Rectified Flow 理论推导

微分方程

像GAN这样的生成模型，它本质上是希望找到一个确定性变换，能将从简单分布（如标准正态分布）采样出来的随机变量，变换为特定数据分布的样本。flow模型也是生成模型之一，它的思路是反过来，先找到一个能将数据分布变换简单分布的可逆变换，再求解相应的逆变换来得到一个生成模型。

传统的flow模型是通过设计精巧的耦合层来实现这个可逆变换，但后来大家就意识到，其实通过微分方程也能实现这个变换，并且理论上还很优雅。基于“神经网络 + 微分方程”做生成模型等一系列研究，构成了被称为“神经ODE”的一个子领域。

考虑 $\boldsymbol{x}_t\in\mathbb{R}^d$ 上的一阶（常）微分方程（组）

\[ \frac{d\boldsymbol{x}_t}{dt}=\boldsymbol{f}_t(\boldsymbol{x}_t) \]

假设 $t\in[0, T]$，那么给定 $\boldsymbol{x}_0$，（在比较容易实现的条件下）我们可以确定地求解出 $\boldsymbol{x}_T$，也就是说该微分方程描述了从 $
\boldsymbol{x}_0$** 到 **$\boldsymbol{x}_T$** 的一个变换。特别地，该变换还是可逆的，即可以逆向求解该微分方程，得到从 **$\boldsymbol{x}_T$** 到 **$\boldsymbol{x}_0$ 的变换。所以说，微分方程本身就是构建可逆变换的一个理论优雅的方案。

直观结果

我们知道，扩散模型是一个 $\boldsymbol{x}_T\to \boldsymbol{x}_0$ 的演化过程，而ODE式扩散模型则指定演化过程按照如下ODE进行：

\[ \begin{equation}\frac{d\boldsymbol{x}_t}{dt}=\boldsymbol{f}_t(\boldsymbol{x}_t)\tag{1}\end{equation} \]

而所谓构建ODE式扩散模型，就是要设计一个函数 $\boldsymbol{f}_t(\boldsymbol{x}_t)$，使其对应的演化轨迹构成给定分布$p_T(\boldsymbol{x}_T)、p_0(\boldsymbol{x}_0)$ 之间的一个变换。说白了，我们希望从 $p_T(\boldsymbol{x}_T)$ 中随机采样一个$\boldsymbol{x}_T$，然后按照上述ODE向后演化得到的 $\boldsymbol{x}_0$ 是 $\sim p_0(\boldsymbol{x}_0)$ 的。

原论文的思路非常简单，随机选定 $\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0),\boldsymbol{x}_T\sim p_T(\boldsymbol{x}_T)$，假设它们按照轨迹

\[ \boldsymbol{x}_t = \boldsymbol{\varphi}_t(\boldsymbol{x}_0, \boldsymbol{x}_T) \]

进行变换。这个轨迹是一个已知的函数，是我们自行设计的部分，理论上只要满足

\[ \boldsymbol{x}_0 = \boldsymbol{\varphi}_0(\boldsymbol{x}_0, \boldsymbol{x}_T),\quad \boldsymbol{x}_T = \boldsymbol{\varphi}_T(\boldsymbol{x}_0, \boldsymbol{x}_T) \]

的连续函数都可以。接着我们就可以写出它满足的微分方程：

\[ \begin{equation}\frac{d\boldsymbol{x}_t}{dt} = \frac{\partial \boldsymbol{\varphi}_t(\boldsymbol{x}_0, \boldsymbol{x}_T)}{\partial t}\end{equation} \]

但这个微分方程是不实用的，因为我们想要的是给定 $\boldsymbol{x}_T$ 来生成$\boldsymbol{x}_0$，但它右端却是$\boldsymbol{x}_0$ 的函数（如果已知 $\boldsymbol{x}_0$ 就完事了），只有像1式那样右端只含有 $\boldsymbol{x}_t$ 的ODE（单从因果关系来看，理论上也可以包含$\boldsymbol{x}_T$，但我们一般不考虑这种情况）才能进行实用的演化。那么，一个直观又“异想天开”的想法是：

学一个函数$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$尽量逼近上式右端！

为此，我们优化如下目标：

\[ \begin{equation}\mathbb{E}_{\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0),\boldsymbol{x}_T\sim p_T(\boldsymbol{x}_T)}\left[\left\Vert \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \frac{\partial \boldsymbol{\varphi}_t(\boldsymbol{x}_0, \boldsymbol{x}_T)}{\partial t}\right\Vert^2\right]\end{equation} \]

由于$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$ 尽量逼近了$\frac{\partial \boldsymbol{\varphi}_t(\boldsymbol{x}_0, \boldsymbol{x}_T)}{\partial t}$ ，所以我们认为将方程2的右端替换为$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$ 也是成立的，这就得到实用的扩散ODE：

\[ \begin{equation}\frac{d\boldsymbol{x}_t}{dt} = \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\end{equation} \]

简单例子

作为简单的例子，我们设$T=1$，并设变化轨迹是直线

\[ \boldsymbol{x}_t = \boldsymbol{\varphi}_t(\boldsymbol{x}_0,\boldsymbol{x}_1) = (\boldsymbol{x}_1 - \boldsymbol{x}_0)t + \boldsymbol{x}_0 \]

那么

\[ \frac{\partial \boldsymbol{\varphi}_t(\boldsymbol{x}_0, \boldsymbol{x}_T)}{\partial t} = \boldsymbol{x}_1 - \boldsymbol{x}_0 \]

所以训练目标 (3) 就是：

\[ \mathbb{E}_{\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0),\boldsymbol{x}_T\sim p_T(\boldsymbol{x}_T)}\left[\left\Vert \boldsymbol{v}_{\boldsymbol{\theta}}\big((\boldsymbol{x}_1 - \boldsymbol{x}_0)t + \boldsymbol{x}_0, t\big) - (\boldsymbol{x}_1 - \boldsymbol{x}_0)\right\Vert^2\right] \]

或者等价地写成

\[ \begin{equation}\mathbb{E}_{\boldsymbol{x}_0,\boldsymbol{x}_t\sim p_0(\boldsymbol{x}_0)p_t(\boldsymbol{x}_t|\boldsymbol{x}_0)}\left[\left\Vert \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \frac{\boldsymbol{x}_t - \boldsymbol{x}_0}{t}\right\Vert^2\right]\end{equation} \]

也是原论文主要研究的模型，被称为“Rectified Flow”。

从这个直线例子的过程也可以看出，通过该思路来构建扩散ODE的步骤只有寥寥几行，相比之前的过程是大大简化了，简单到甚至让人有种“颠覆了对扩散模型的印象”的不可思议之感。

证明过程

然而，迄今为止前面“直观结果”一节的结论只能算是一个直观的猜测，因为我们还没有从理论上证明优化目标 (2) 所得到的方程 (3) 的确实现了分布 $p_T(\boldsymbol{x}_T)、p_0(\boldsymbol{x}_0)$之间的变换。

为了证明这一结论，笔者一开始是想证明目标 (2) 的最优解满足连续性方程：

\[ \frac{\partial p_t(\boldsymbol{x}_t)}{\partial t} = -\nabla_{\boldsymbol{x}_t}\cdot\big(p_t(\boldsymbol{x}_t)\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\big) \]

如果满足，那么根据连续性方程与ODE的对应关系，方程 (3) 确实是分布 $p_T(\boldsymbol{x}_T)、p_0(\boldsymbol{x}_0)$之间的一个变换。

但仔细想一下，这个思路似乎有点迂回了，因为根据文章《测试函数法推导连续性方程和Fokker-Planck方程》，连续性方程本身就是由ODE通过

\[ \begin{equation}\mathbb{E}_{\boldsymbol{x}_{t+\Delta t}}\left[\phi(\boldsymbol{x}_{t+\Delta t})\right] = \mathbb{E}_{\boldsymbol{x}_t}\left[\phi(\boldsymbol{x}_t + \boldsymbol{f}_t(\boldsymbol{x}_t)\Delta t)\right]\end{equation} \]

推出的，所以按理说 (5) 更基本，我们只需要证明 (2) 的最优解满足它就行。也就是说，我们想要找到一个纯粹是 $\boldsymbol{x}_t$ 的函数 $\boldsymbol{f}_t(\boldsymbol{x}_t)$ 满足 (5)，然后发现它正好是 (2) 的最优解。

于是，我们写出（简单起见，$\boldsymbol{\varphi}_t(\boldsymbol{x}_0,\boldsymbol{x}_T)$简写为$\boldsymbol{\varphi}_t$）

\[ \begin{aligned} \mathbb{E}_{\boldsymbol{x}_{t+\Delta t}}\left[\phi(\boldsymbol{x}_{t+\Delta t})\right] =&\, \mathbb{E}_{\boldsymbol{x}_0, \boldsymbol{x}_T}\left[\phi(\boldsymbol{\varphi}_{t+\Delta t})\right] \\ =&\, \mathbb{E}_{\boldsymbol{x}_0, \boldsymbol{x}_T}\left[\phi(\boldsymbol{\varphi}_t) + \Delta t\,\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\cdot\nabla_{\boldsymbol{\varphi}_t}\phi(\boldsymbol{\varphi}_t)\right] \\ =&\, \mathbb{E}_{\boldsymbol{x}_0, \boldsymbol{x}_T}\left[\phi(\boldsymbol{x}_t)\right] + \Delta t\,\mathbb{E}_{\boldsymbol{x}_0, \boldsymbol{x}_T}\left[\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\cdot\nabla_{\boldsymbol{x}_t}\phi(\boldsymbol{x}_t)\right] \\ =&\, \mathbb{E}_{\boldsymbol{x}_t}\left[\phi(\boldsymbol{x}_t)\right] + \Delta t\,\mathbb{E}_{\boldsymbol{x}_0, \boldsymbol{x}_T}\left[\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\cdot\nabla_{\boldsymbol{x}_t}\phi(\boldsymbol{x}_t)\right] \\ \end{aligned} \]

其中第一个等号是因为式$\boldsymbol{x}_t = \boldsymbol{\varphi}_t(\boldsymbol{x}_0, \boldsymbol{x}_T)$，第二个等号是泰勒展开到一阶，第三个等号同样是式$\boldsymbol{x}_t = \boldsymbol{\varphi}_t(\boldsymbol{x}_0, \boldsymbol{x}_T)$，第四个等号就是因为$\boldsymbol{x}_t$是$\boldsymbol{x}_0,\boldsymbol{x}_T$的确定性函数，所以关于$\boldsymbol{x}_0,\boldsymbol{x}_T$的期望就是关于$\boldsymbol{x}_t$的期望。

我们看到，$\frac{\partial \boldsymbol{\varphi}_t}{\partial t}$ 是 $\boldsymbol{x}_0,\boldsymbol{x}_T$ 的函数，接下来我们再做一个假设：式 $\boldsymbol{x}_t = \boldsymbol{\varphi}_t(\boldsymbol{x}_0, \boldsymbol{x}_T)$ 关于 $\boldsymbol{x}_T$ 是可逆的。这个假设意味着我们可以从中解出$\boldsymbol{x}_T=\boldsymbol{\psi}_t(\boldsymbol{x}_0,\boldsymbol{x}_t)$，这个结果可以代入$\frac{\partial \boldsymbol{\varphi}_t}{\partial t}$，使它变为$\boldsymbol{x}_0,\boldsymbol{x}_t$ 的函数。所以我们有

\[ \begin{aligned} \mathbb{E}_{\boldsymbol{x}_{t+\Delta t}}\left[\phi(\boldsymbol{x}_{t+\Delta t})\right] =&\, \mathbb{E}_{\boldsymbol{x}_t}\left[\phi(\boldsymbol{x}_t)\right] + \Delta t\,\mathbb{E}_{\boldsymbol{x}_0, \boldsymbol{x}_T}\left[\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\cdot\nabla_{\boldsymbol{x}_t}\phi(\boldsymbol{x}_t)\right] \\ =&\, \mathbb{E}_{\boldsymbol{x}_t}\left[\phi(\boldsymbol{x}_t)\right] + \Delta t\,\mathbb{E}_{\boldsymbol{x}_0, \boldsymbol{x}_t}\left[\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\cdot\nabla_{\boldsymbol{x}_t}\phi(\boldsymbol{x}_t)\right] \\ =&\, \mathbb{E}_{\boldsymbol{x}_t}\left[\phi(\boldsymbol{x}_t)\right] + \Delta t\,\mathbb{E}_{\boldsymbol{x}_t}\left[\underbrace{\mathbb{E}_{\boldsymbol{x}_0|\boldsymbol{x}_t}\left[\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\right]}_{\boldsymbol{x}_t\text{的函数}}\cdot\nabla_{\boldsymbol{x}_t}\phi(\boldsymbol{x}_t)\right] \\ =&\, \mathbb{E}_{\boldsymbol{x}_t}\left[\phi\left(\boldsymbol{x}_t + \Delta t\,\mathbb{E}_{\boldsymbol{x}_0|\boldsymbol{x}_t}\left[\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\right]\right)\right] \end{aligned} \]

其中第二个等号是因为$\frac{\partial \boldsymbol{\varphi}_t}{\partial t}$ 已经改为 $\boldsymbol{x}_0,\boldsymbol{x}_t$ 的函数，所以第二项期望的随机变量改为$\boldsymbol{x}_0,\boldsymbol{x}_t$；第三个等号则是相当于做了分解$p(\boldsymbol{x}_0,\boldsymbol{x}_t)=p(\boldsymbol{x}_0|\boldsymbol{x}_t)p(\boldsymbol{x}_t)$ ，此时 $\boldsymbol{x}_0,\boldsymbol{x}_t$ 不是独立的，所以要注明$\boldsymbol{x}_0|\boldsymbol{x}_t$，即 $\boldsymbol{x}_0$ 是依赖于 $\boldsymbol{x}_t$ 的。注意 $\frac{\partial \boldsymbol{\varphi}_t}{\partial t}$ 原本是 $\boldsymbol{x}_0,\boldsymbol{x}_t$ 的函数，现在对$\boldsymbol{x}_0$ 求期望后，剩下的唯一自变量就是$\boldsymbol{x}_t$，后面我们会看到它就是我们要找的纯粹是$\boldsymbol{x}_t$的函数！第四个等号，就是利用泰勒展开公式将两项重新合并起来。

现在，我们得到了

\[ \mathbb{E}_{\boldsymbol{x}_{t+\Delta t}}\left[\phi(\boldsymbol{x}_{t+\Delta t})\right] = \mathbb{E}_{\boldsymbol{x}_t}\left[\phi\left(\boldsymbol{x}_t + \Delta t\,\mathbb{E}_{\boldsymbol{x}_0|\boldsymbol{x}_t}\left[\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\right]\right)\right] \]

对于任意测试函数 $\phi$ 成立，所以这意味着

\[ \begin{equation}\boldsymbol{x}_{t+\Delta t} = \boldsymbol{x}_t + \Delta t\,\mathbb{E}_{\boldsymbol{x}_0|\boldsymbol{x}_t}\left[\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\right]\quad\Rightarrow\quad\frac{d\boldsymbol{x}_t}{dt} = \mathbb{E}_{\boldsymbol{x}_0|\boldsymbol{x}_t}\left[\frac{\partial \boldsymbol{\varphi}_t}{\partial t}\right]\end{equation} \]

就是我们要寻找的ODE。根据

\[ \mathbb{E}_{\boldsymbol{x}}[\boldsymbol{x}] = \mathop{\text{argmin}}_{\boldsymbol{\mu}}\mathbb{E}_{\boldsymbol{x}}\left[\Vert \boldsymbol{x} - \boldsymbol{\mu}\Vert^2\right] \]

式 (6) 的右端正好是训练目标 (2) 的最优解，这就证明了优化训练目标 (2) 得出的方程 (3) 的确实现了分布 $p_T(\boldsymbol{x}_T)、p_0(\boldsymbol{x}_0)$ 之间的变换。

Rectified Flow 具体解释

问题-传输映射（将一个分布搬运到另一个分布）

我们先定义好要解决的问题。无论是从噪声生成图片(generative modeling)，还是将人脸转化为猫脸 (domain transfer)，都可以这样概括成将一个分布转化成另一个分布的问题：

给定从两个分布 $π_0$ 和 $π_1 (中的采样，我们希望找到一个传输映射 \(T$ 使得*，当 *\)Z_0 \sim \pi_0\) 时， $Z_1 = T(Z_0) \sim \pi_1$。

比如，在生成模型里， $Z_0 \sim \pi_0$ 是高斯噪声分布， $π_1$ 是数据的分布(比如图片), 我们想找到一个方法，把噪声 $Z_0$ 映射成一个服从 $π_1$ 的数据 $Z_1$。在数据迁移（domain transfer）里， $Z_0$, $Z_1$ 分别是人脸和猫脸的图片。所以这个问题是生成模型和数据迁移的统一表述。

在我们的框架下，映射 $T$ 是通过以下连续运动系统，也就是一个常微分方程(ordinary differential equation (ODE))，或者叫流模型(flow)，来隐式定义的：

\[ \frac{d}{dt} Z_t = v(Z_t, t)，~Z_0\sim \pi_0， \forall t \in [0,1] \]

我们可以想象从 $π_0$ 里采样出来的 $Z_0$ 是一个粒子。它从 $t=0$ 时刻开始连续运动，在 $t$ 时刻以 $v(Z_t,t)$ 为速度。直到 $t=1$ 时刻得到 $Z_1$。我们希望 $Z_1$ 服从分布 $π_1$ 。这里我们假设 $v(Zt,t)$ 是一个神经网络。我们的任务是从数据里学习出 $v(Z_t,t)$ 来达到 $Z_1\sim \pi_1$ 的目的。

走直线，走得快

除了希望 $Z_1 \sim \pi_1$, 我们还希望这个连续运动系统能够在计算机里快速地模拟出来。注意到，在实际计算过程中，上面的连续系统通常是用Euler法(或其变种)在离散化的时间上近似：

\[ Z_{t+\epsilon} = Z_t + \epsilon v(Z_t, t)， \]

这里 $ϵ$ 是一个步长参数。我们需要适当的选择 $ϵ$ 来平衡速度和精度： $ϵ$ 需要足够小来保证近似的精度，但同时小的 $ϵ$ 意味着我们从 t=0 到 t=1要跑很多步，速度就慢。

那么问题来了，什么样的系统能最快地用Euler法来模拟呢？也就是说，什么样的体系能允许我们在用较大的步长 ϵ的同时还能得到很好的精度呢？

答案是“走直线”。如下图所示，如果粒子的运动轨迹是弯曲的，我们需要很细的离散化来得到很好的结果。如果粒子的轨迹是直线，那么即使我们取最大的步长($ϵ=1$)，只用一步走到 $t=1$ 时刻, 还是能得到正确的结果! 所以，我们希望我们学习出来的速度模型 $v$ 既能保证 $Z_1 \sim \pi_1$, 又能给出尽量直的轨迹。怎么同时实现这两个目的在数学上是一个非常不简单(non-trivial)的问题，涉及最优传输（optimal transport）的一些深刻理论。但是我们发现其实可以用一个非常简单的方法来解决这个问题。

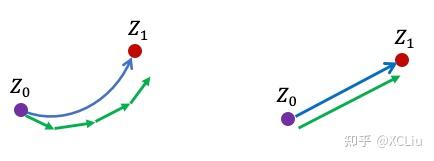
Rectified Flow-基于直线ODE学习生成模型

假设我们有从两个分布中的采样 $X_0 \sim \pi_0$，$X_1 \sim \pi_1$ (比如 $X_0$ 是从 $π_0$ 里出来的随机噪声， $X_1$ 是一个随机的数据(服从 $π_1$))。我们把 $X_0$ 和 $X_1$ 用一个线性插值连接起来，得到

\[ X_t = t X_1 + (1-t) X_0,~~t \in [0,1]. \]

这里 $X_0$ 和 $X_1$ 是随机，或者说，以任意方式配对的。你也许觉得$X_0$ 和 $X_1$ 应该用一种有意义的方式配对好，这样能够得到更好的效果。我们先忽略这个问题，待会回来解决它。

现在，如果我们拿 $X_t$ 对时间 $t $求导，我们其实已经可以得到一个能够将数据从 $X_0\sim \pi_0$ 传输到 $X_1\sim \pi_1$ 的"ODE"了,

\[ \frac{d}{d t} X_t = X_1 - X_0,~~~~~~ \forall t \in [0,1]. \]

但是，这个"ODE"并不实用而且很奇怪，所以要打个引号：它不是一个“因果”(causal)，或者“可前向模拟”(forward simulatable)的系统，因为要计算 $X_t$ 在 $t$ 时刻的速度 $(X_1 - X_0)$ 需要提前(在 $t<1$时)知道ODE轨迹的终点 $X_1$。如果我们都已经知道 $X_1$ 了，那其实也就没有必要模拟ODE了。

那么我们能不能学习 $v$ ，使得我们想要的“可前向模拟”的ODE $\frac{d}{dt}Z_t = v(Z_t, t)$ 能尽可能逼近刚才这个“不可前向模拟”的过程呢？最简单的方法就是优化 $v$ 来最小化这两个系统的速度函数（分别是 $v$ 和 $X_1-X_0$ ）之间的平方误差：

\[ \displaystyle \min_{v} \int_{0}^1 \mathbb{E}_{X_0 \sim \pi_0, X_1 \sim \pi_1} \left[|| (X_1 -X_0) - v(X_t, t) ||^2\right] d t,~~~\text{where}~~~X_t = t X_1 + (1-t) X_0. \]

这是一个标准的优化任务。我们可以将 $v$ 设置成一个神经网络，并用随机梯度下降或者Adam来优化，进而得到我们的可模拟ODE模型。

这就是我们的基本方法。数学上，我们可以证明这样学出来的 v 确实可以保证生成想要的分布 $Z_1 \sim \pi_1$。对数学感兴趣的同学可以看一看论文里的理论推导。下面我们只用这个图来给一些直观的解释。

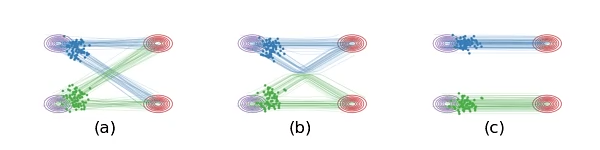
图(a)：在我们用直线连接 $X_0$ 和 $X_1$ 时，有些线会在中间的地方相交，这是导致 $\frac{d}{dt} X_t = X_1 - X_0$ 非因果的原因(在交叉点，$X_t$ 既可以沿蓝线走，也可以沿绿线走，因此粒子不知该向岔路的哪边走)。

💡 训练过程是随机噪声训练至目标图像，噪声的随机性使得训练是无约束的多对多，$π_0$ 的粒子$x_{01}$能到$π_1$的粒子$x_{11}$，也能到π1的粒子$x_{12}$，反之$π_1$的粒子$x_{11}$能由$π_0$的粒子$x_{01}$获得，也能由$π_0$的粒子$x_{02}$获得，这对应了运动图a；

图(b)：我们学习出的ODE因为必须是因果的，所以不能出现道路相交的情况，它会在原来相交的地方把道路交换成不交叉的形式。这样，我们学习出来的ODE仍然保留了原来的基本路径，但是做了一个重组来避免相交的情况。这样的结果是，图(a)和图(b)里的系统在每个时刻 t的边际分布是一样的，即使总体的路径不一样。

💡 ode保证速度场是连续平滑的，所以在粒子在$x_t$处的速度$v_t$是唯一的，所以模型在训练交叉点的方向v的时候产生了困惑模型最终会让它往“平均方向”走也就是在sample时图b中的粒子走到交叉点处会“横着走”的原因但是为什么又会折回去呢？因为当它横着走了一段之后粒子所在的“位置”在训练时就是一个确定的方向那个方向就是“折反回去”的方向

我们的方法起名为Rectified Flow。这里rectified是“拉直”，“规整”的意思。我们这个框架其实也可以用来推导和解释其他的扩散模型(如DDPM)。我们论文里有详细说明，这里就不赘述了。我们现在的算法版本应该是在已知的算法空间里最简单的选项了。我们提供了Colab Notebook来帮助大家通过实践来理解这个过程。

Reflow-拉直轨迹，一步生成

因为Rectified Flow要在直线轨迹的交叉点做路径重组，所以上面的ODE模型(或者说flow)的轨迹仍然可能是弯曲的 (如上面的图(b))，不能达到一步生成。我们提出一个“Reflow”方法，将ODE的轨迹进一步变直。

具体的做法非常简单: 假设我们从 $\pi_0$ 里采样出一批 $X_0$ 。然后，从 $X_0$ 出发，我们模拟上面学出的flow(叫它1-Rectified Flow)，得到$X_1 = \text{Flow}_1(X_0)$ 。我们用这样得到的 $(X_0, X_1)$ 对来学一个新的"2-Rectified Flow"：

\[ \displaystyle \min_{v} \int_{0}^1 \mathbb{E}_{{X_0\sim \pi_0, X_1=\text{Flow}_1(X_0)}} \left[|| (X_1 - X_0) - v(X_t, t) ||^2\right] d t,~~~\text{with}~~~X_t = t X_1 + (1-t) X_0. \]

这里，2-Rectified Flow和1-Rectified Flow在训练过程中唯一的区别就是数据配对不同：在1-Rectified Flow中， $X_0$与 $X_1$ 是随机或者任意配对的；在2-Rectified Flow中， $X_0$与 $X_1$ 是通过1-Rectified Flow配对的。上面的动图中，图(c)展示了Reflow的效果。因为从1-Rectified Flow里出来的 $(X_0,X_1)$ 已经有很好的配对, 他们的直线插值交叉数减少，所以2-Rectified Flow的轨迹也就（比起1-Rectified Flow）变得很直了(虽然仔细看还不完美)。理论上，我们可以重复Reflow多次，从而得到3-Rectified Flow, 4-Rectified Flow... 我们可以证明这个过程其实是在单调地减小最优传输理论中的传输代价(transport cost)，而且最终收敛到完全直的状态。当然，实际中，因为每次 $v$ 优化得不完美，多次Reflow会积累误差，所以我们不建议做太多次的Reflow。幸运的是，在我们的实验中，我们发现对生成图片和很多我们感兴趣的问题而言，像上面的图(c)一样，1次Reflow已经可以得到非常直的轨迹了，配合蒸馏足够达到一步生成的效果了。