问题:两条平行线可以相交于一点
在欧氏几何空间,同一平面的两条平行线不能相交,这是我们都熟悉的一种场景。
然而,在透视空间里面,两条平行线可以相交,例如:火车轨道随着我们的视线越来越窄,最后两条平行线在无穷远处交于一点。

欧氏空间(或者笛卡尔空间)描述2D/3D几何非常适合,但是这种方法却不适合处理透视空间的问题(实际上,欧氏几何是透视几何的一个子集合),2维笛卡尔坐标可以表示为\((x,y)\)。
如果一个点在无穷远处,这个点的坐标将会\((∞,∞)\),在欧氏空间,这变得没有意义。
平行线在透视空间的无穷远处交于一点,但是在欧氏空间却不能,数学家发现了一种方式来解决这个问题。
方法:齐次坐标
简而言之,齐次坐标就是用\(N+1\)维来代表\(N\)维坐标
我们可以在一个2D笛卡尔坐标末尾加上一个额外的变量\(w\) 来形成2D齐次坐标,因此,一个点\((X,Y)\) 在齐次坐标里面变成了\((x,y,w)\) ,并且有
\[X = \frac{x}{w} \qquad Y = \frac{y}{w}\]
例如,笛卡尔坐标系下\((1,2)\)的齐次坐标可以表示为\((1,2,1)\),如果点\((1,2)\)移动到无限远处,在笛卡尔坐标下它变为\((∞,∞)\),然后它的齐次坐标表示为\((1,2,0)\),因为\((1/0, 2/0) = (∞,∞)\),我们可以不用”\(∞\)"来表示一个无穷远处的点了。
为什么叫齐次坐标?
我们把齐次坐标转化为笛卡尔坐标的方法是前面\(n-1\)个坐标分量分别除以最后一个分量即可。
\[\underset{\text{Homogeneous}}{(x, y, w)} \quad \Leftrightarrow \quad \underset{\text{Cartesian}}{\left( \frac{x}{w}, \frac{y}{w} \right)}
\]
转化齐次坐标到笛卡尔坐标的过程中,我们有一个发现,例如:
\[\begin{aligned}
(1, 2, 3) \quad &\Rightarrow \quad \left( \frac{1}{3}, \frac{2}{3} \right) \\
(2, 4, 6) \quad &\Rightarrow \quad \left( \frac{2}{6}, \frac{4}{6} \right) = \left( \frac{1}{3}, \frac{2}{3} \right) \\
(4, 8, 12) \quad &\Rightarrow \quad \left( \frac{4}{12}, \frac{8}{12} \right) = \left( \frac{1}{3}, \frac{2}{3} \right) \\
&\vdots \\
(1a, 2a, 3a) \quad &\Rightarrow \quad \left( \frac{1a}{3a}, \frac{2a}{3a} \right) = \left( \frac{1}{3}, \frac{2}{3} \right)
\end{aligned}
\]
你会发现\((1, 2, 3)\), \((2, 4, 6)\) 和\((4, 8, 12)\)对应同一个Euclidean point \((1/3, 2/3)\),任何标量的乘积,例如\((1a, 2a, 3a)\) 对应 笛卡尔空间里面的\((1/3, 2/3)\) 。因此,这些点是“齐次的”,因为他们代表了笛卡尔坐标系里面的同一个点。换句话说,齐次坐标有规模不变性。
证明:两条直线可以相交
考虑如下方程组:
\[\begin{cases}
Ax + By + C = 0 \\
Ax + By + D = 0
\end{cases}
\]
我们知道在笛卡尔坐标系里面,该方程组无解,因为\(C ≠ D,\)如果\(C=D\),两条直线就相同了。 让我们在透视空间里面,用齐次坐标\(x/w,\) \(y/w\)代替\(x\) ,\(y\)
\[\begin{cases}
A \frac{x}{w} + B \frac{y}{w} + C = 0 \\
A \frac{x}{w} + B \frac{y}{w} + D = 0
\end{cases}
\quad \Rightarrow \quad
\begin{cases}
Ax + By + Cw = 0 \\
Ax + By + Dw = 0
\end{cases}
\]
现在我们有一个解\((x, y, 0)\),两条直线相交于\((x, y, 0)\),这个点在无穷远处。
坐标变换
前面我们提到了图像的缩放变换和旋转变换,可以用矩阵乘法的形式来表达变换后的像素位置映射关系。
那么,对于平移变换呢?平移变换表示的是位置变化的概念。如下图所示,一个图像矩形从中心点\([x1,y1]\)平移到了中心点\([x2,y2]\)处,整体大小和角度都没有变化。在\(x\)方向和\(y\)方向上分别平移了\(tx\)和\(ty\)大小。
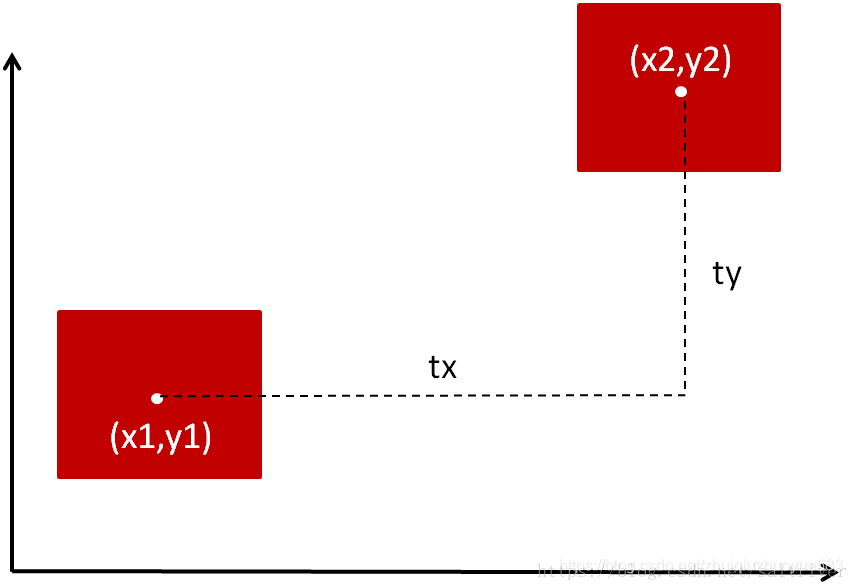
显然:
\[x2=x1+tx\\y2=y1+ty\]
这对于图像中的每一个点都是成立的。写成矩阵的形式就是:
\[\begin{bmatrix} x2 \\ y2 \end{bmatrix} = \begin{bmatrix} x1 \\ y1 \end{bmatrix} + \begin{bmatrix} tx \\ ty \end{bmatrix}
\]
我们再把前面的缩放变换和旋转变换的矩阵形式写出来:
缩放变换:
\[\begin{bmatrix} x2 \\ y2 \end{bmatrix} = \begin{bmatrix} k_x & 0 \\ 0 & k_y \end{bmatrix} \begin{bmatrix} x1 \\ y1 \end{bmatrix}
\]
旋转变换:
\[\begin{bmatrix} x2 \\ y2 \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x1 \\ y1 \end{bmatrix}
\]
我们注意到,缩放变换和旋转变换都可以表示成矩阵乘法的形式。实际上,图像的几何变换通常不是单一的,也就是说经常性的缩放、旋转、平移一起变换。例如先放大2倍,然后旋转45度,然后再缩小0.5倍。那么就可以表示成矩阵乘法串接的形式:
\[\begin{bmatrix} x2 \\ y2 \end{bmatrix} = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \begin{bmatrix} \cos 45 & -\sin 45 \\ \sin 45 & \cos 45 \end{bmatrix} \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} \begin{bmatrix} x1 \\ y1 \end{bmatrix}
\]
这样,不管有多少次变换,都可以用矩阵乘法来实现。但是平移变换呢?从前面看到,平移变换并不是矩阵乘法的形式,而是矩阵加法的形式!
那能不能把缩放变换、旋转变换、平移变换统一成矩阵乘法的形式呢,这样不管进行多少次变换,都可以表示成矩阵连乘的形式,将极大的方便计算和降低运算量
这种方法就是“升维”,引入“齐次坐标”,将图像从平面2D坐标变成3D坐标。我们看看平移变换的矩阵形式:
\[\begin{bmatrix} x2 \\ y2 \end{bmatrix} = \begin{bmatrix} x1 \\ y1 \end{bmatrix} + \begin{bmatrix} tx \\ ty \end{bmatrix}
\]
将其升维,变成3维,上式就可以表示成:
\[\begin{bmatrix} x2 \\ y2 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & tx \\ 0 & 1 & ty \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x1 \\ y1 \\ 1 \end{bmatrix}
\]
这是个非常优美的地方,学习过矩阵乘法的同学可以算一下右边的式子,是否最终结果与前面是一样的。
这样,平移变换通过升维后的齐次坐标,也变成了矩阵乘法的形式。当然缩放变换和旋转变换的矩阵形式也得改一改,统一变成3维的形式。
缩放变换:
\[\begin{bmatrix} x2 \\ y2 \\ 1 \end{bmatrix} = \begin{bmatrix} k_x & 0 & 0 \\ 0 & k_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x1 \\ y1 \\ 1 \end{bmatrix}
\]
旋转变换:
\[\begin{bmatrix} x2 \\ y2 \\ 1 \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x1 \\ y1 \\ 1 \end{bmatrix}
\]
终于统一了。以后所有的变换,不管怎样变换,变换多少次,都可以表示成一连串的矩阵相乘了,这是多么的方便。
这就是引入齐次坐标的作用,把各种变换都统一了起来,即 把缩放,旋转,平移等变换都统一起来,都表示成一连串的矩阵相乘的形式。保证了形式上的线性一致性。
小结
齐次坐标就是将一个原本是\(n\)维的向量用一个\(n+1\)维向量来表示。
许多图形应用涉及到几何变换,主要包括平移、旋转、缩放。以矩阵表达式来计算这些变换时,平移是矩阵相加,旋转和缩放则是矩阵相乘,综合起来可以表示为 \(x=R∗X+t\)(注:因为习惯的原因,实际使用时一般使用变化矩阵左乘向量)(\(R \)旋转缩放矩阵,\(t \)为平移矩阵,\(X\)为原向量,\(x \)为变换后的向量)。
引入齐次坐标的目的主要是合并矩阵运算中的乘法和加法,表示为\(x=P∗X\)的形式。即它提供了用矩阵运算把二维、三维甚至高维空间中的一个点集从一个坐标系变换到另一个坐标系的有效方法。
Reference
为什么要引入齐次坐标,齐次坐标的意义(一)
为什么要引入齐次坐标,齐次坐标的意义(二)

