简介
PnP(Perspective-n-Point)是求解3D到2D点对运动的方法,目的是求解相机坐标系相对世界坐标系的位姿。它描述了已知\(n\)个3D点的坐标(相对世界坐标系)以及这些点的像素坐标时,如何估计相机的位姿(即求解世界坐标系到相机坐标系的旋转矩阵\(R\)和平移向量\(t\))。
用数学公式描述如下:
基本公式:
其中,\(\boldsymbol{p}\)为点在像素坐标系下的坐标,\(P^C\)为点在相机坐标系下的坐标,\(P^W\)为点在世界坐标系下的坐标,\(\omega\)为点的深度,\(K\)为相机的内参矩阵,\(R_{CW}\)和\(t^C_{CW}\)为从世界坐标系到相机坐标系的位姿转换。
已知:\(n\)个点在世界坐标系下的坐标\(P_1^W,P_2^W,...,P_n^W\),这些点相应在像素坐标系下的坐标\(\boldsymbol{p}_1,\boldsymbol{p}_2,...,\boldsymbol{p}_n\),相机内参矩阵\(K\)。由于是已知\(n\)个点的3D-2D对应关系,所以相应问题被称作PnP问题。
求解:相机坐标系相对于世界坐标系的位姿,即\(P^C=R_{CW}\times P^W+\boldsymbol{t^C_{CW}}\)中的\(R_{CW}\)和\(\boldsymbol{t^C_{CW}}\)。\(R_{CW}\)是世界坐标系到相机坐标系的旋转矩阵(将同一个向量在世界坐标系下的表示转化为在相机坐标系下的表示),\(\boldsymbol{t^C_{CW}}\)为相应的平移向量(即从相机坐标系原点指向世界坐标系原点的向量,在相机坐标系下的表示)。
算法:直接线性变换(DLT)、P3P、EPnP、光束法平差(BA,Bundle Adjustment)。
符号介绍
本文中,一律用上标区别向量在不同坐标系下的表达,\(P^W=[X^W,Y^W,Z^W]^T\)代表点在世界坐标系下的表示,\(P^C=[X^C,Y^C,Z^C]^T\)代表点在相机坐标系下的表示,\(P^{'}=[X^C/Z^C,Y^C/Z^C,1]^T=[u_1,v_1,1]^T\)代表点在相机归一化坐标系下的表示,\(\boldsymbol{p}=[u,v,1]^T\)代表点在像素坐标系下的表示(投影到像素平面之后扩展为齐次坐标)。
上述坐标系间的转换关系如下:\(\omega \boldsymbol{p}=KP^C=K(R_{CW}\times P^W+t^C_{CW})\),其中\(\omega = Z^C\)为点在相机坐标系下的深度。
展开:
PnP就是在已知\(n\)个点的像素坐标\(p_i\)及其世界坐标系下的坐标\(P^W_i\)和相机的内参矩阵\(K\)的前提下,求解相机的位姿\(R\)和\(t\)。
算法总结
直接线性变换(DLT,Direct Linear Transform):
为了通过一个点的像素坐标和世界坐标构建一个关于相机位姿参数的方程,我们可以先通过相机内参将像素坐标转换为相机归一化坐标,根据相应的归一化约束条件可以获得关于姿态参数的两个方程,为了求解\(R\)和\(t\)中一共的12个参数,我们至少需要6个点来构建方程。
根据关系
可得
最初,我们已知点的像素坐标\(\begin{pmatrix}u\\v \\1\end{pmatrix}\),将其左乘相机内参矩阵的逆\(K^{-1}\)可得点在相机归一化坐标系中的坐标
相机归一化坐标系中的坐标乘以点相对于成像平面的深度\(\omega=Z^C\)可得点相对于相机坐标系的坐标:
根据\(P^{C}=[R|t]P^W\),可构建等式:
利用最后一行把\(\omega\)消去,可得两个约束:
为简化表示,定义增广矩阵\(T=[R|t]\)的行向量表示:
所以说,有:
注意上式中:\(\boldsymbol{t}\)是待求的变量;\(\boldsymbol{P^W},u_1,v_1\)是已知量,分别为点在世界坐标系下的3D位置以及在相机归一化坐标系下的2D投影位置(可通过点的像素坐标左乘相机内参矩阵的逆得到)。可以看出,每个特征点提供了两个关于\(\boldsymbol{t}\)的线性约束。假设一共有\(N\)个特征点,则可列出如下线性方程组:
记为\(A\boldsymbol{t}=0\),注意上式中点的坐标省去了上标\(^W\),它们都是点在世界坐标系下的表示。
\(\boldsymbol{t}\)一共有12维,最少通过6对匹配点即可实现增广矩阵\(\boldsymbol{T=[R|t]}\)的线性求解,这种方法称为DLT。当1匹配点的数量大于6对时,可以使用SVD等方法求超定方程的最小二乘解。针对SVD求超定方程的最小二乘解,说明如下:当匹配点数量大于6对时,可以获得一个在\(|\boldsymbol{t}|=1\)约束下的最小二乘解\(\boldsymbol{t^*}=\underset{\boldsymbol{t}}{argmin}||A\boldsymbol{t}||\)。
具体的,令\(A=UDV^T\),则最小二乘解\(\boldsymbol{t^*}\)为\(V\)的最后一列\(\boldsymbol{t^v}\),这样求得的最小二乘解是没有尺度的,之后可以再利用SVD确定最优旋转矩阵近似以及相应的尺度,便可以确定最终的相机姿态\(T=[R|t]\)。
P3P
P3P利用3个点的几何关系,通过三对点已知的世界坐标系下的3D坐标以及相应点在相机归一化平面上投影的2D坐标,可以通过构建方程得到三个点在相机坐标系下的3D坐标,之后将问题转化为3D-3D的ICP问题,由于带有匹配信息的3D-3D位姿求解非常容易,所以这种方法是有效的。
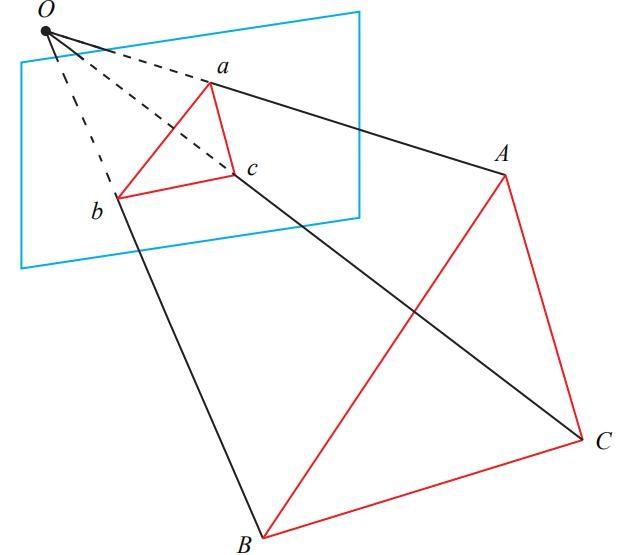
上图中,我们记3D点为A,B,C,2D点为a,b,c(注意2D点为3D点在相机归一化平面上的投影),我们需要通过一些几何关系构建方程得到OA、OB、OC,来得到3D点在相机坐标系下的坐标(其实就是获取归一化平面上2D点的深度信息)。
对于三组对应的三角形:
由余弦定理:
对以上三式全体除以\(OC^2\),并记\(x=OA/OC,y=OB/OC\),可得:
由上式中的后两式可知,若能解出\(x,y\),则代入后两式中的任一式,即可得到\(OC\),之后再由\(x,y\)计算出\(OA,OB\),便可以知道三个点在相机坐标系下的坐标。
为求解出\(x,y\),记
有:
将第一个式子中得到的\(v\)代入后两式,可得:
上面两个方程中,由于我们知道点的相机归一化坐标,即2D投影位置,则三个余弦\(cos<a,b>,cos<b,c>,cos<a,c>\)是已知的。同时,\(u=BC^2/AB^2,w=AC^2/AB^2\)可以通过三个点在世界坐标系下的坐标算出。该式中只有\(x,y\)是未知的,随着相机的移动会发生改变。所以,该方程组是关于\(x,y\)的一个二元二次方程,求该方程的解析解需要用到吴消元法,这个解法在参考文献[4]里有详细介绍。该方程最多可能有四个解,我们可以使用验证点来计算最可能的解,得到\(A,B,C\)在相机坐标系下的3D坐标,之后使用ICP计算相机的位姿\(R,t\)。
P3P利用3个点的几何关系,通过三对点已知的世界坐标系下的3D坐标以及相应点在相机归一化平面上投影的2D坐标,可以通过构建方程得到三个点在相机坐标系下的3D坐标,之后将问题转化为3D-3D的ICP问题,由于带有匹配信息的3D-3D位姿求解非常容易,所以这种方法是有效的。
但P3P同样存在一些问题:
- P3P值利用3个点的信息,当给定的匹配点多于3组时,难以利用更多的信息。
- 如果3D点或2D点受到噪声影响,或者存在误匹配,则算法失效。
EPnP:
EPnP的思路和P3P差不多,相对P3P来说,EPnP利用更多的信息,用迭代的方式对相机位姿进行优化,以尽可能消除噪声的影响。但主体思路都是先得到相应点在相机坐标系下的坐标,将3D-2D问题转换为3D-3D问题,再利用ICP求解。
EPnP算法利用已知的\(n\)个3D点的世界坐标,通过PCA选择4个控制点(世界坐标已知),建立新的局部坐标系,从而将3D点的世界坐标用新的控制点(世界坐标)表示出来。然后,利用相机投影模型和2D点像素坐标,建立关于控制点在相机坐标系下坐标的线性方程组,求解出4个控制点在相机坐标系下的坐标,进而求解出\(n\)个3D点在相机坐标系下的坐标。到了这里,我们已知\(n\)个3D点在世界坐标系下和相机坐标系下的坐标,问题转换为3D-3D问题,利用ICP求解即可。
在本节中,\(n\)个3D参考点在世界坐标系下的坐标分别为\(\boldsymbol{p}^w_i,i=1,2,...,n\),在相机坐标系下的坐标分别为\(\boldsymbol{p}^c_i,i=1,2,...,n\)。我们选择的4个控制点,在世界坐标系下的坐标分别为 \(\boldsymbol{c}^w_j,j=1,2,3,4\), 在相机坐标系下的坐标分别为\(\boldsymbol{c}^w_j,j=1,2,3,4\) 。
EPnP将\(n\)个参考点中的每一个表示为4个控制点的加权和:
同理,相机坐标系下也有:
\(n\)个参考点的世界坐标\(\boldsymbol{p}^w_i\)我们是已知的,四个参考点是我们人为选择的,其世界坐标\(\boldsymbol{c}^w_j\)可以认为是已知的,加权系数\(\alpha_{ij}\)可以利用参考点和控制点的世界坐标很方便的计算出来。那么唯一需要我们计算的未知量就是4个控制点在相机坐标系下的坐标,其可以根据相机投影模型和\(n\)个参考点的2D像素坐标构建线性方程组计算。之后我们便得到了\(n\)个参考点在世界坐标系和相机坐标系下的坐标,问题便被转化为ICP问题。
接下来我们依次解决上面一段所述EPnP算法框架中的细节问题:
- 关系\(\boldsymbol{p}^c_i=\sum_{j=1}^{4}\alpha _{ij}\boldsymbol{c}^c_j\)为什么成立?
- 为什么控制点要选择4个?
- 4个控制点该如何选择?
- 4个控制点在相机坐标系下的坐标如何计算?
由于
因此关系\(\boldsymbol{p}^c_i=\sum_{j=1}^{4}\alpha _{ij}\boldsymbol{c}^c_j\)成立,在上面的推导过程中,我们用到了非常重要的约束条件\(\sum_{j=1}^{4}\alpha _{ij}=1\)。如果没有这个约束条件,上述推导将不成立,我们也无法得到相机坐标系下参考点和控制点的关系。
正是由于约束条件\(\sum_{j=1}^{4}\alpha _{ij}=1\)必须被精确的满足,我们在选择控制点时必须选择4个而不是3个。
假如我们仅选择3个控制点,那么我们可以列出方程:
一共三个未知量确有四个方程,这是一个超定方程组,只存在最小二乘意义上的解。换句话,在一般情形下,不存在精确满足4个方程的解。即约束不一定能被精确的满足。
在选择4个控制点的情形下:
可以精确解出:
在选择控制点时,原则上只要矩阵\(C\)可逆即可,四个控制点不共面即可。参考文献[5]中给出了更加精细选择控制点的方法,可以参考。
之后我们进行最重要的一步,即计算4个控制点在相机坐标系下的坐标:
由相机模型,我们可以得到:
上式中有\(\boldsymbol{c}^c_j=(x^c_j,y^c_j,z^c_j)^T\)。我们可以得到两个线性方程:
把所有\(n\)个点结合起来,可以得到关于4个控制点共12个坐标的线性方程组,解数值方程。最后还需要利用空间点在外参变换下,空间关系不改变的约束,即\(||\boldsymbol{c}^w_i-\boldsymbol{c}^w_j||^2=||\boldsymbol{c}^c_i-\boldsymbol{c}^c_j||^2\),结合非线性优化来得到最终的控制点在相机坐标系下的坐标。
得到4个控制点在相机坐标系下的坐标之后,我们便可以计算\(n\)个参考点在相机坐标系下的坐标。有了\(n\)个3D参考点在相机坐标系和世界坐标系下的坐标之后,我们将问题转化为3D-3D问题,利用ICP求解即可。
光束法平差(BA,Bundle Adjustment):
上面的方法都是线性的,我们还可以把PnP问题构建为一个关于重投影误差的非线性最小二乘问题。线性方法往往是通过将空间点的位置看做已知量,通过构建方程组求解相机位姿。而非线性优化则将相机位姿和空间点位置都看成优化变量,放在一起优化,这也是BA的另一个名字:捆集优化的由来(个人理解)。这种方法将相机位姿和三维点位置放在一起进行重投影误差最小化的优化,是一种整体的优化方法。
假设我们有n个三维空间点,其世界坐标系下的坐标为\(\boldsymbol{P}^W_i=[X^W_i,Y^W_i,Z^W_i]^T(i=1,2,...,n)\),相应点在像素坐标系下的齐次坐标为\(\boldsymbol{p}_i=[u_i,v_i,1]^T(i=1,2,...,n)\)。假设相机位姿已知且观测点没有噪声,则两者之间存在以下关系:
其矩阵形式为:
上式中隐含了一次从齐次坐标到非齐次坐标的转换,其中\(\omega_i\)为点在相机坐标系下的深度,\(K\)为相机内参矩阵,\(T\)为世界坐标系到相机坐标系的变换矩阵。
但由于相机位姿未知以及观测点存在一定噪声误差,该式并不严格成立。因此,为了求解出最优的相机位姿,我们构建最小二乘问题,将\(n\)个观测点对应的误差求和,寻找最优的相机位姿,使得总的误差最小化:
上式中的误差,是将观测到的像素坐标系下的投影坐标与通过相机位姿和3D点位置计算得到的像素坐标系下的投影坐标做差,称为重投影误差。一般来说,我们计算误差时使用非齐次坐标,即像素坐标系两个轴方向上的误差,故误差只有两维。在实际问题中,我们通过特征匹配得到了像素坐标系下的\(\boldsymbol{p}_i\)和世界坐标系下的\(\boldsymbol{P}^W_i\)是同一个空间点的两种不同表达形式,但是不知道相机位姿\(T\),所以一开始观测到的像素坐标\(\boldsymbol{p}_i\)和通过位姿计算投影得到的计算值\(\frac{1}{\omega_i }\boldsymbol{KTP}^W_i\)并不重合,两者之间有一定的距离,我们通过调整相机位姿的估计值,使得这个距离变小。因为我们有很多对空间点的匹配关系,这个相机位姿估计值的调整需要同时考虑很多对点,这也就使得最后的效果是整体误差的缩小,而每一对点的误差都不会精确为0。
在调整相机位姿的估计值使得整体误差变小的过程中,最重要的是要知道误差相对于相机位姿的导数,知道了导数才能确定相机位姿估计值调整的方向,导数即误差项关于优化变量的导数,也就是线性化:
其中的雅克比矩阵\(\boldsymbol{J^T}\)的解析形式是问题的关键。目前,\(\boldsymbol{e}\)为像素误差(2维),\(\boldsymbol{x}\)为相机位姿(6维),\(\boldsymbol{J^T}\)是一个\(2\times 6\)的矩阵。
之后将应用扰动模型来通过李代数求解误差相对于位姿的导数。由于旋转矩阵自身带有约束,作为优化变量会引入额外的约束,使问题变得困难。通过李群—李代数之间的转换关系,我们可以把位姿估计变成无约束的优化问题,简化求解方式。
记空间点在相机坐标系下的坐标为\(P^C=[X^C,Y^C,Z^C]^T\),则有\(\omega \boldsymbol{p}=KP^C\),利用相机模型可知:
上式中的\(u,v\)均为根据相机位姿计算而来的像素坐标,通过下标表明。我们定义的误差为观测值减计算值(预测值),即
通过定义相机坐标系下坐标这一中间变量,我们可以很方便的通过链式法则求解误差的变化关于位姿扰动量的导数:
上式中第一项是误差关于投影点的导数,根据上文相机模型中得到的关系,可得:
第二项为变换到相机坐标系后的点关于李代数的导数,可得:
注意我们采用的是非齐次坐标,所以上式中只保留了矩阵的前三维。
将上面两项相乘,就可以得到最终版\(2\times 6\) 的雅克比矩阵:
上式中的雅克比描述了重投影误差关于相机位姿李代数的一阶变化关系。前面的负号是由于我们的误差是由观测值减计算值(预测值)定义的,如果反过来,将误差定义成“预测值减观测值”的形式,只需要去掉前面的负号即可。此外,如果李代数\(se(3)\)的定义方式是旋转在前,平移在后,则只需要将该矩阵的前3列与后3列对调即可。
除了优化相机位姿之外,我们还希望优化特征点的空间位置,因此还需要讨论误差\(\boldsymbol{e}\)关于空间点\(\boldsymbol{P}^W\)的导数,这个导数相对来说推导较为简单:
上式中第一项已经推出,推导第二项时,按照定义,有\(\boldsymbol{P}^C=R\boldsymbol{P}^W+t\),则\(\boldsymbol{P}^C\)对\(\boldsymbol{P}^W\)求导之后只剩下\(R\).
所以,我们得到误差向量关于空间点位置的导数为:
上面我们导出了重投影误差向量关于相机位姿与特征点位置的两个导数矩阵。这两个导数矩阵十分重要,能够在优化迭代调整相机位姿估计值的过程中,提供重中之重的梯度方向,指导优化的迭代。
下面是具体的优化迭代过程:
每一次迭代时,对于每一个空间点,先将空间点在世界坐标系下的坐标变换到相机坐标系下,在通过相机内参得到像素坐标的计算值,将像素坐标的观测值与计算值做差,得到误差向量\(\boldsymbol{e}_i\),同时得到雅克比矩阵\(\boldsymbol{J}^T_i\)。对每个点计算出其对应的误差向量和雅克比矩阵之后,可以得到\(\boldsymbol{H}=\sum_{i=1}^n\boldsymbol{J}_i\boldsymbol{J}^T_i\),\(\boldsymbol{b}=-\sum_{i=1}^n\boldsymbol{J}_i\boldsymbol{e}_i\),通过解线性方程组\(\boldsymbol{H}\boldsymbol{\Delta x}=\boldsymbol{b}\),得到位姿的变化量\(\boldsymbol{\Delta x}\),则变化之后的位姿为:\(\xi ^{'}=exp(\boldsymbol{\Delta x})\xi\),如此不断迭代,当\(\boldsymbol{\Delta x}\)范数足够小时停止迭代。
下面是高翔老师在《视觉SLAM14讲》中提供的手写Gauss-Newton法进行位姿估计的相关代码:
void bundleAdjustmentGaussNewton(
const VecVector3d &points_3d,
const VecVector2d &points_2d,
const Mat &K,
Sophus::SE3d &pose)
{ //传入空间点点,空间点像素坐标,内参; 初始pose,此程序中初始pose为0;
typedef Eigen::Matrix<double, 6, 1> Vector6d;
const int iterations = 10;
double cost = 0, lastCost = 0;
double fx = K.at<double>(0, 0);
double fy = K.at<double>(1, 1);
double cx = K.at<double>(0, 2);
double cy = K.at<double>(1, 2);
for (int iter = 0; iter < iterations; iter++) { //进行迭代
Eigen::Matrix<double, 6, 6> H = Eigen::Matrix<double, 6, 6>::Zero();
Vector6d b = Vector6d::Zero();
cost = 0;
// compute cost
for (int i = 0; i < points_3d.size(); i++) {
Eigen::Vector3d pc = pose * points_3d[i];//得到空间点在相机坐标系下的坐标
// Vector6d se3 = pose.log();
// cout<<"se3 = "<<se3.transpose()<<endl;一开始se3为0,三四次迭代后趋于稳定
double inv_z = 1.0 / pc[2];
double inv_z2 = inv_z * inv_z;
Eigen::Vector2d proj (fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);//P点像素坐标
//的投影计算值
Eigen::Vector2d e = points_2d[i] - proj;//作差,得到差值;是观测值-预测值!
cost += e.squaredNorm();//误差的二范数的平方
Eigen::Matrix<double, 2, 6> J;//2*6的雅克比矩阵,即误差相对于位姿求导,通过导数可以知道有了误
//差以后我们应该往哪个方向去优化
J << -fx * inv_z,
0,
fx * pc[0] * inv_z2,
fx * pc[0] * pc[1] * inv_z2,
-fx - fx * pc[0] * pc[0] * inv_z2,
fx * pc[1] * inv_z,
0,
-fy * inv_z,
fy * pc[1] * inv_z,
fy + fy * pc[1] * pc[1] * inv_z2,
-fy * pc[0] * pc[1] * inv_z2,
-fy * pc[0] * inv_z;
H += J.transpose() * J;//高斯牛顿方法,H*dx=b
b += -J.transpose() * e;
}
Vector6d dx;
dx = H.ldlt().solve(b);//对H做LDLT分解,并求解dx
cout <<"dx:" << endl << dx <<endl;
cout <<"dx.norm():" << endl << dx.norm() <<endl;
if (isnan(dx[0])) {
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost >= lastCost) {
// cost increase, update is not good//发散的情况
cout << "cost: " << cost << ", last cost: " << lastCost << endl;
break;
}
// update your estimation
pose = Sophus::SE3d::exp(dx) * pose;
lastCost = cost;
cout << "iteration " << iter << " cost=" << cout.precision(12) << cost << endl;
if (dx.norm() < 1e-6) {
// converge 当dx<1e-6时停止迭代
break;
}
}
cout << "pose by g-n: \n" << pose.matrix() << endl;
}
四种算法总结:
每种算法用一句话概括:
- DLT:根据\(n\)个点的世界坐标和相机归一化平面坐标,最后一行用于消去深度,得到\(2n\)个约束方程,利用SVD求解超定方程并得到位姿矩阵的估计。
- P3P:根据3个点的世界坐标和相机归一化平面坐标,利用余弦定理几何关系,得到3个点的相机坐标,将问题转化为3D-3D位姿估计并利用ICP求解,最后还需要一对点用于验证。
- EPnP:根据\(n\)个点的世界坐标选择4个控制点并计算加权系数,通过相机模型和\(n\)个点的像素坐标求解4个控制点在相机坐标系下的坐标,进而得到\(n\)个点在相机坐标系下的坐标,将问题转化为3D-3D位姿估计并利用ICP求解。
- BA:根据对应点的重投影误差构建非线性优化问题,利用李代数得到误差关于位姿的导数以指导优化方向,不断迭代求得所有对应点重投影误差之和最小的位姿估计。