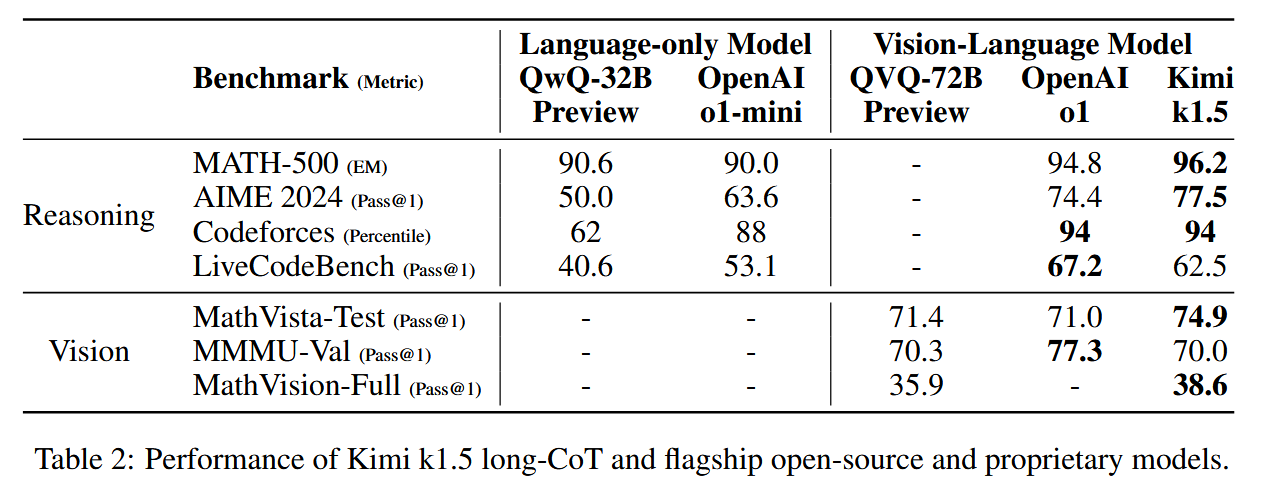
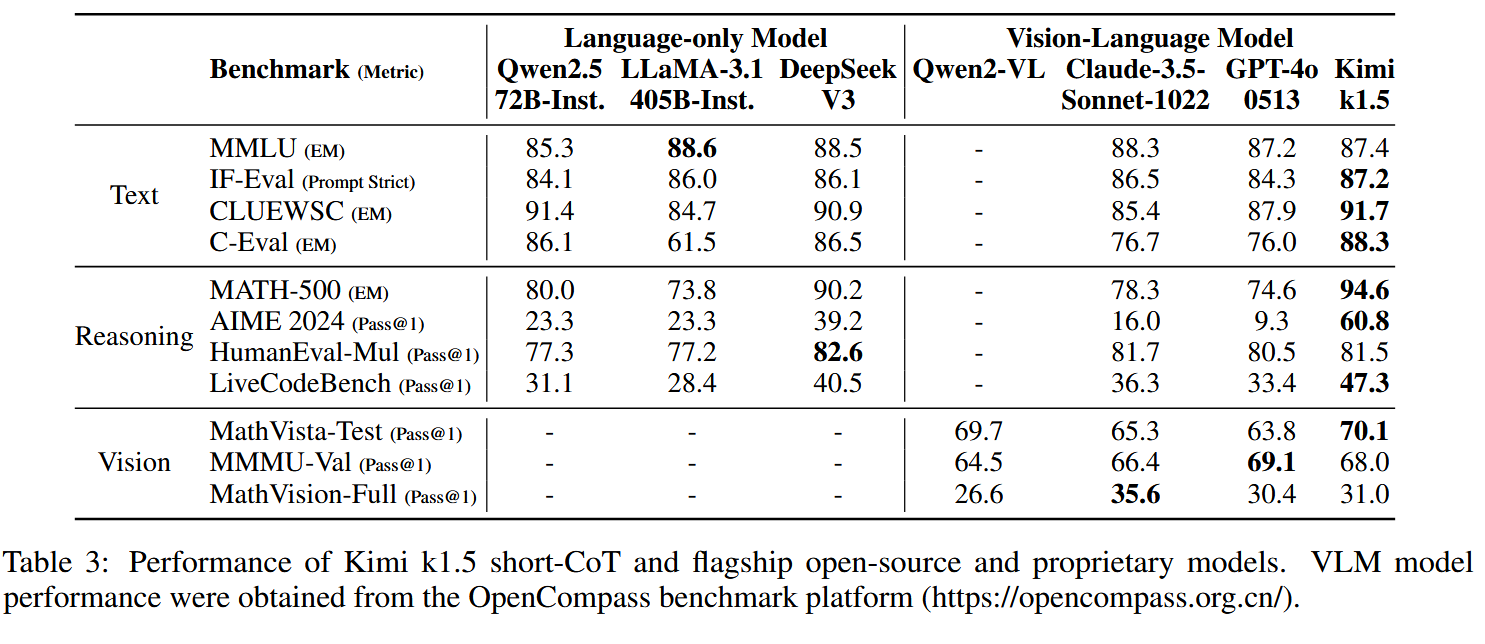
概述

Kimi k1.5采用了一种简化而有效的强化学习框架，其核心在于长上下文扩展和改进的策略优化方法，而不依赖于更复杂的技术如蒙特卡洛树搜索、价值函数和过程奖励模型。

问题设定

给定训练数据集 \(D = \{(x_i, y^*_i)\}_{i=1}^n\)，其中包含问题 \(x_i\) 和对应的真实答案 \(y^*_i\)，目标是训练一个策略模型 \(\pi_\theta\) 来准确解决测试问题。在复杂推理场景中，思维链(CoT)方法提出使用一系列中间步骤 \(z = (z_1, z_2, ..., z_m)\) 来连接问题 \(x\) 和答案 \(y\)，每个 \(z_i\) 是解决问题的重要中间步骤。

当解决问题 \(x\) 时，思维 \(z_t \sim \pi_\theta(\cdot|x, z_1, ..., z_{t-1})\) 被自回归采样，最终答案 \(y \sim \pi_\theta(\cdot|x, z_1, ..., z_m)\)。

强化学习目标

基于真实答案 \(y^*\)，分配一个值 \(r(x, y, y^*) \in \{0, 1\}\), Kimi k1.5使用奖励模型 \(r\) 来评估给定问题 \(x\) 的提出答案 \(y\) 的正确性。

给定一个问题 \(x\)，模型 \(\pi_\theta\) 生成CoT和最终答案：\(z \sim \pi_\theta(\cdot|x)\)，\(y \sim \pi_\theta(\cdot|x, z)\)。生成的CoT质量通过它是否能导致正确的最终答案来评估。总结起来，考虑以下目标来优化策略：

\[ \max_\theta \mathbb{E}_{(x,y^*)\sim D, (y,z)\sim\pi_\theta} [r(x, y, y^*)] \]

策略优化方法

在线策略镜像下降（Online Policy Mirror Descent）

Kimi k1.5应用了在线策略镜像下降的变体作为训练算法。该算法迭代执行。在第 \(i\) 次迭代中，使用当前模型 \(\pi_{\theta_i}\) 作为参考模型，优化以下相对熵正则化的策略优化问题：

\[ \max_\theta \mathbb{E}_{(x,y^*)\sim D} \left[\mathbb{E}_{(y,z)\sim\pi_\theta} [r(x, y, y^*)] - \tau KL(\pi_\theta(x)||\pi_{\theta_i}(x))\right] \]

其中 \(\tau > 0\) 是控制正则化程度的参数.

这个目标有一个闭式解：

\[ \pi^*(y, z|x) = \pi_{\theta_i}(y, z|x) \exp(r(x, y, y^*)/\tau)/Z \]

其中 \(Z = \sum_{y',z'} \pi_{\theta_i}(y', z'|x) \exp(r(x, y', y^*)/\tau)\) 是归一化因子。

对两边取对数，我们得到对于任何 \((y, z)\)，以下约束成立，这允许我们在优化过程中利用off-policy数据：

\[ r(x, y, y^*) - \tau \log Z = \tau \log \frac{\pi^*(y, z|x)}{\pi_{\theta_i}(y, z|x)} \]

这启发了以下代理损失：

\[ L(\theta) = \mathbb{E}_{(x,y^*)\sim D}\left[\mathbb{E}_{(y,z)\sim\pi_{\theta_i}}\left[\left(r(x, y, y^*) - \tau \log Z - \tau \log \frac{\pi_\theta(y, z|x)}{\pi_{\theta_i}(y, z|x)}\right)^2\right]\right] \]

为了近似 \(\tau \log Z\)，使用样本 \((y_1, z_1), ..., (y_k, z_k) \sim \pi_{\theta_i}\)：

\[ \tau \log Z \approx \tau \log \frac{1}{k}\sum_{j=1}^k \exp(r(x, y_j, y^*)/\tau) \]

研究发现，使用采样奖励的经验均值 \(\bar{r} = \text{mean}(r(x, y_1, y^*), ..., r(x, y_k, y^*))\) 可以产生有效的实际结果。最终，通过取代理损失的梯度来得出学习算法。对于每个问题 \(x\)，使用参考策略 \(\pi_{\theta_i}\) 采样 \(k\) 个响应，梯度为：

\[ \frac{1}{k}\sum_{j=1}^k \nabla_\theta \log \pi_\theta(y_j, z_j|x)(r(x, y_j, y^*) - \bar{r}) - \frac{\tau}{2} \nabla_\theta\left(\log \frac{\pi_\theta(y_j, z_j|x)}{\pi_{\theta_i}(y_j, z_j|x)}\right)^2 \]

与传统策略梯度方法的相似性与区别

对于熟悉策略梯度方法的人来说，Kimi k1.5的梯度公式看起来类似于使用采样奖励均值作为基线的策略梯度方法(公式2)。然而，存在两个主要区别：

off-policy 采样：响应是从参考策略 \(\pi_{\theta_i}\) 采样的，而不是从当前策略(on-policy)采样。这是一个重要的区别，因为传统的策略梯度方法通常是on-policy，即使用当前策略生成样本。
L2正则化：应用了L2正则化，这增加了优化的稳定性。
因此，Kimi k1.5 的方法可以被视为将常规的 on-policy 正则化策略梯度算法自然扩展到off-policy情况。他们从数据集D中采样一批问题，并将参数更新为 \(\theta_{i+1}\)，该参数随后作为下一次迭代的参考策略。由于每次迭代由于参考策略的变化而考虑不同的优化问题，他们也在每次迭代开始时重置优化器。

另外，Kimi k1.5在训练系统中排除了价值网络，这一设计选择在之前的研究中也有应用。虽然这显著提高了训练效率，但研究人员也提出了一个假设：传统使用价值函数进行信用分配在经典强化学习中的方法可能不适合他们的上下文。

为了说明这一点，他们提供了一个具体场景：

假设模型已经生成了部分思维链(CoT) \((z_1, z_2, ..., z_t)\)，现在面临两个潜在的下一步推理：\(z_{t+1}\) 和 \(z'_{t+1}\)。
假设 \(z_{t+1}\) 直接导致正确答案，而 \(z'_{t+1}\) 包含一些错误。
如果有一个理想的价值函数，它会指示 \(z_{t+1}\) 比 \(z'_{t+1}\) 具有更高的价值。
根据标准的信用分配原则，选择 \(z'_{t+1}\) 会受到惩罚，因为它相对于当前策略具有负面优势。
然而，研究人员认为，探索 \(z'_{t+1}\) 对于训练模型生成长CoT实际上非常有价值。通过使用从长CoT得出的最终答案的合理性作为奖励信号，只要模型成功恢复并达到正确答案，就可以从取 \(z'_{t+1}\)中学习试错模式。从这个例子中得出的关键是，我们应该鼓励模型探索不同的推理路径，以增强其解决复杂问题的能力。这种探索性方法产生了丰富的经验，支持关键规划技能的发展。我们的主要目标不仅限于在训练问题上获得高准确性，而是专注于为模型提供有效的问题解决策略，最终提高其在测试问题上的性能。

总结一下K1.5的强化框架：

off-policy 学习框架：通过从参考策略采样并应用L2正则化，扩展了传统策略梯度方法。
无价值网络设计：不使用价值网络进行信用分配，而是鼓励探索多样化推理路径，即使这些路径可能包含错误。这种方法有助于模型学习更复杂的推理策略，包括试错和恢复能力。
这种设计理念反映了一个更广泛的哲学：在复杂推理任务中，探索和多样性比短期奖励最大化更重要，因为它们能够培养更强大的问题解决能力。

独特优势

长上下文扩展
简化框架
长度惩罚

Long2short

虽然长思维链(Long-CoT)模型能够实现强大的性能，但与标准的短思维链(Short-CoT)大语言模型相比，它在测试时消耗更多的令牌(tokens)。然而，通过将长思维链模型的思考先验知识转移到短思维链模型，即使在有限的测试时间令牌预算下，性能也可以得到改善。这就是所谓的"Long2Short"问题。

Kimi k1.5团队提出了几种解决Long2Short问题的方法，包括模型合并、最短拒绝采样、DPO和Long2Short强化学习。这些方法旨在保持长CoT模型的推理能力，同时提高令牌效率。

模型合并 (Model Merging)
最短拒绝采样 (Shortest Rejection Sampling)
DPO (Direct Preference Optimization)
Long2Short强化学习 (Long2Short RL)

RL Infrastructure

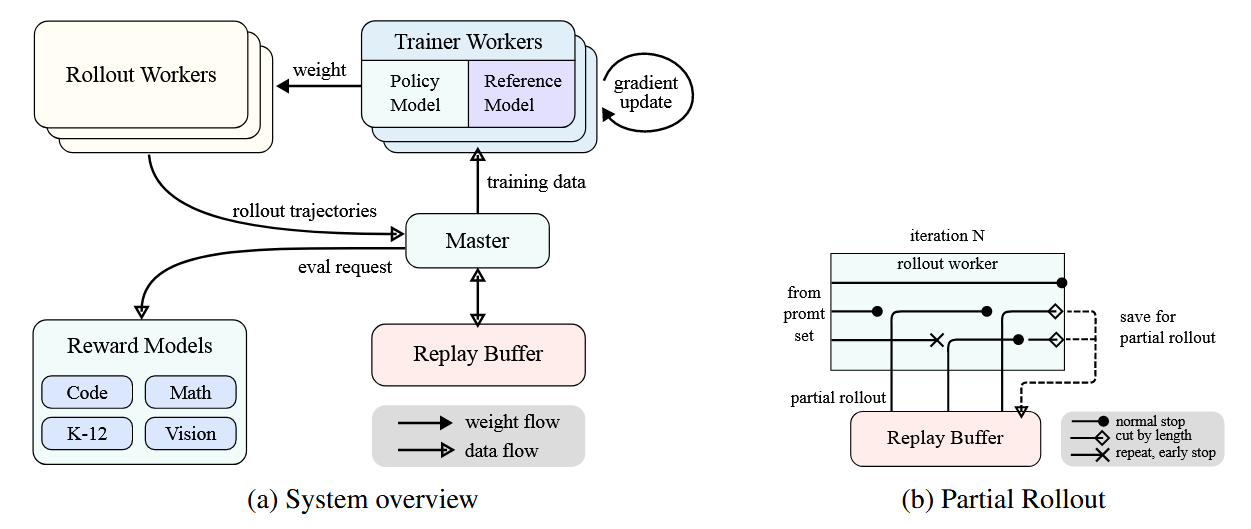
Kimi k1.5系统采用了一个精心设计的迭代同步RL框架，旨在通过持续学习和适应来增强模型的推理能力。该系统的一个关键创新是引入了部分展开(Partial Rollout)技术，专门设计用于优化复杂推理轨迹的处理。

如图a所示，RL训练系统通过迭代同步方法运行，每次迭代包括展开阶段和训练阶段：

展开阶段：
训练阶段：
中央主控：
训练工作流程：
代码执行服务：

Kimi k1.5—CoT强化训练