最近，似乎现在每个大型语言模型（LLM）和新闻中提到的复杂神经网络架构都使用略有不同的激活函数，而就在几年前，最常见的做法只是在神经网络的内部层中使用 ReLU。
曾经优秀的 ReLUs 怎么了，以及是什么促使最新的大型语言模型（LLMs）的创造者们开始使用不同的（更高级的）激活函数？
**Threshold activation (Perceptron) **
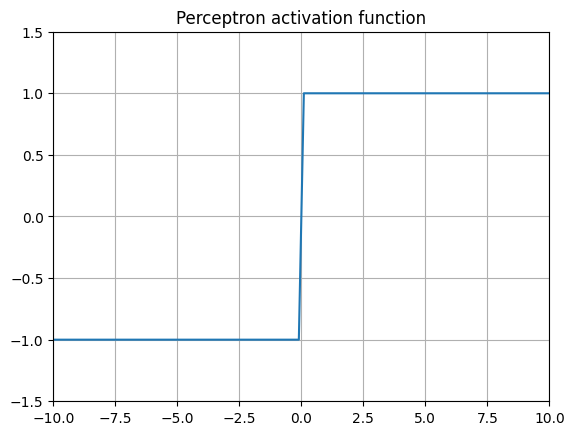
1957 年，罗森布拉特建造了“感知机”
最古老的激活函数是基本感知器。它由芝加哥大学精神病学系的爱德华·麦克洛奇和沃尔特·皮茨构思，后来由弗兰克·罗森布拉特在 1957 年于康奈尔航空实验室为美国海军在硬件上更著名地实现了。该算法非常简单，其基本规则是：如果某个值超过某个阈值，则返回 1，否则返回 0。有些变体会返回 1 或-1。
由于其二元特性，除了某一点外，其导数为 0。这意味着权重无法通过反向传播等技术与网络提供的标签成比例地缩放。
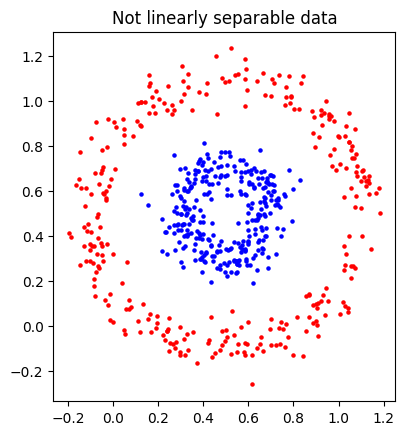
多层感知器会简化为线性函数，使得它难以处理非线性可分的数据，比如这两个甜甜圈点云。
Sigmoid
logistic 函数实际上起源于 19 世纪，自 20 世纪 40 年代随着逻辑回归作为一般统计工具的发展，已被应用于分类问题。
值得注意的是，这是 1986 年 David Rumelhart、Geoffrey Hinton 和 Ronald Williams 在推广反向传播的论文中使用的函数。 有趣的是，这篇论文实际上受到了 DNA 结构共同发现者 Francis Crick 的非议，认为其生物学上不可行。
Sigmoid 函数具有几个特性，使其在分类任务中非常有效。首先，它是一个光滑的可微函数，这对于反向传播是必要的。其次，该函数是非线性的。第三，该函数将值压缩在 0 和 1 之间，使我们能够将输出解释为概率。前两个特性是使多层逻辑“神经网络”能够分离非线性不可分数据的关键。
然而，使用 sigmoid 函数作为深度神经网络每一层的激活函数存在一个关键问题。当远离 0 时，sigmoid 函数的导数会变得非常小。在反向传播通过多层时，我们实际上是在对导数进行求导，从而使得梯度越来越小，越来越远离 0。这会导致梯度实际上“消失”，从而使得训练过程基本上停滞不前。
Softmax
softmax 函数是对 sigmoid 函数在多分类情况下的推广，由 John Bridle 在 1989 年的一篇论文中推广（尽管该函数本身要古老得多，因为它本质上是玻尔兹曼分布的概率分布）。当 K=2 时，这个函数基本上会简化为“正类”的 sigmoid 函数。
tanh（Hyperbolic Tangent）
或
或
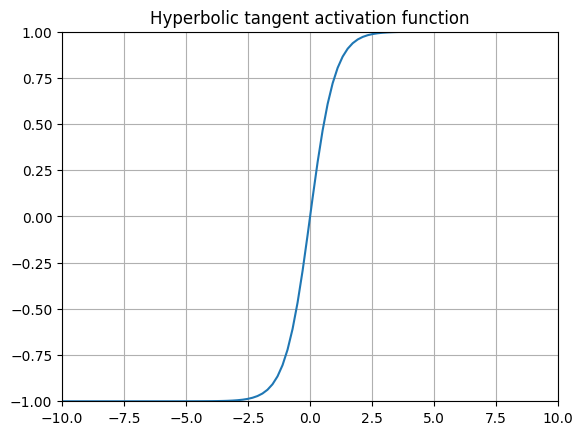
原始的 MNIST 论文在每一层都使用了 tanh！
双曲正切函数是常见的替代 sigmoid 函数的方法，最著名的是在 Yann Lecunn 1989 年的手写数字识别论文（原始 MNIST 论文）中使用过。这个函数也因其作为许多循环神经网络（RNNs）变体的门控函数而广为人知。
出于纯粹的好奇心，我通过谷歌搜索来确定 PyTorch 底层使用的是哪个公式，因为文档暗示它使用的是第二个公式。我认为它实际上通过 std::tanh 在底层使用 glibc ，并且有一些相当有趣的优化。1993 年对 tanh 的 glibc 高度优化的实现根据 x 是否真的很小、小于 1 或大于 22，使用四种不同的计算方式！
使用 tanh 与 softmax 一样，都存在相同的问题，即远离 的导数非常小，导致梯度消失问题。
多年来，梯度消失问题一直阻碍了进展，直到应用了…
ReLU (Rectified Linear Unit)
或者
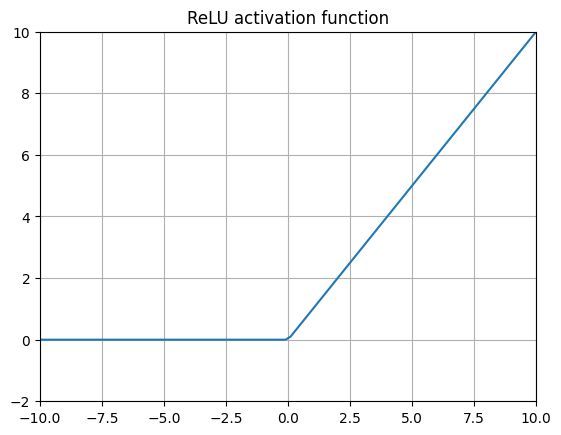
将 RELUs 应用于神经网络在 Nair 和 Hinton (2010) 的研究中，某种程度上开启了当前深度学习的革命。通过用这种极其简单的函数替换神经网络内部层的 Sigmoid 函数，梯度消失问题得到了有效解决，从而使得创建更深层的神经网络成为可能。
但这具体是如何工作的呢？激活函数难道不是应该连续且可平滑求导才能起作用吗？ReLU 在 \(x=0\) 处甚至不可导！实际上这并不是什么大问题，使用 ReLU 的计算效率提升非常值得肯定。ReLU 的梯度在值小于 0 时为 0，大于 0 时为 1，大多数库会将梯度在 \(x=0\) 处设为 0。这使得 ReLU 是目前计算效率最高的激活层，完全无需指数运算，而指数运算会显著降低计算速度。ReLU 在许多许多复杂的机器学习任务中表现良好，在 2016 年之前，它被用于几乎所有深度神经网络的内部层（包括 AlphaGo）。
然而，ReLU 的表达能力可能对性能有限制，具体来说是因为所有负值都被简单地钳位为 0。这引出了……
**Leaky ReLU (Leaky Rectified Linear Unit) **
或者
也称为 LReLU，有时也称为 PReLU（参数化 ReLU），以强调负值斜率的 alpha 参数可以手动调整。
该层通过允许负输入值以某个常数为系数传播到下一层来解决 ReLU 的一个缺点。Leaky ReLU 试图通过为负值使用较小的斜率来获得更好的性能，但在实践中，这种斜率的选择可能相当任意。
使用负斜率的选择意味着高度负的值会持续变得越来越负，这引导我们……
ELU (Exponential Linear Unit)
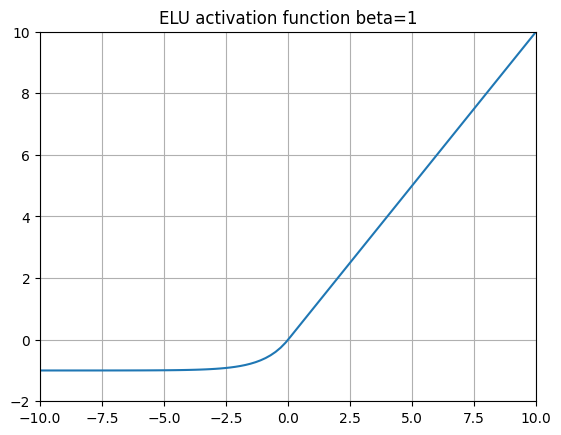
ELU（指数线性单元） 采用了 LeakyReLUs 的思想，并将负斜率替换为指数函数 \(\alpha (e^x - 1)\)。这意味着当 \(x\) 越来越负时， \(y\) 将收敛到 \(-\alpha\) 。
2015 年，ELU 论文的作者在 ImageNet 上用 ELU 激活函数替换 ReLU 时展示了优异的性能。
GELU (Gaussian Error Linear Unit)
其中 \(\Phi(x)\) 是标准高斯累积分布函数（CDF）。
\(x\) 服从均值为 0、标准差为 1 的正态分布。另外，通常用“QuickGELU”来近似。例如，在 CLIP 的源代码中：
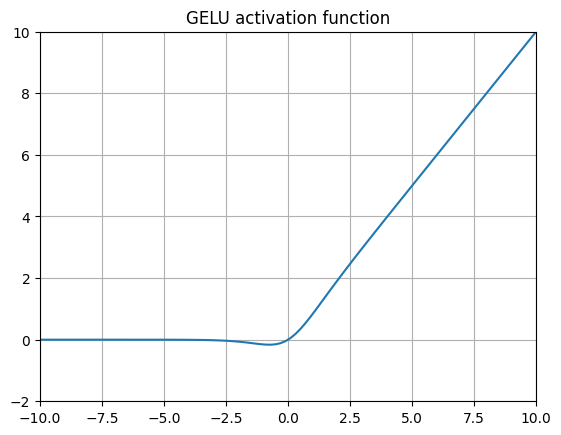
2016 年引入的 GELUs（以及在同一篇论文中出现的 SiLUs）可能是当今最典型的非 ReLU 激活函数。核心思想是，当我们预期层的输入呈正态分布时（例如使用批量归一化时），给定输入变量 \(x\) 的 CDF 表示该输入小于或等于观测输入的概率。因此 \(x * \Phi(x)\) 简单地根据其正态分布的概率对输入 \(x\) 进行缩放。
从函数本身的形状来看，比较这个函数（类似于 SiLU、Swish 和 SoLU）的表达能力与 Leaky ReLU 和 ELU 很有趣。这里我们允许一些负值通过，但当 \(x\) 变得非常负时，值会逐渐被钳制在 0，而 Leaky ReLUs 中的值会简单地越来越小，ELUs 中的值会收敛到 \(-\alpha\) 。GELUs 避免了梯度消失问题，同时仍然允许一些负值通过。
GELU 被用于 GPT-3 、BERT 以及原始 CLIP 论文，还用于 OpenAI 的一系列模型。实际上，由于 QuickGELU 近似的常用，GeLU 与 SiLU/Swish-1 非常相似，唯一区别在于对 Sigmoid 函数的 x 输入进行缩放。
**SiLU (Sigmoid Weighted Linear Unit) **
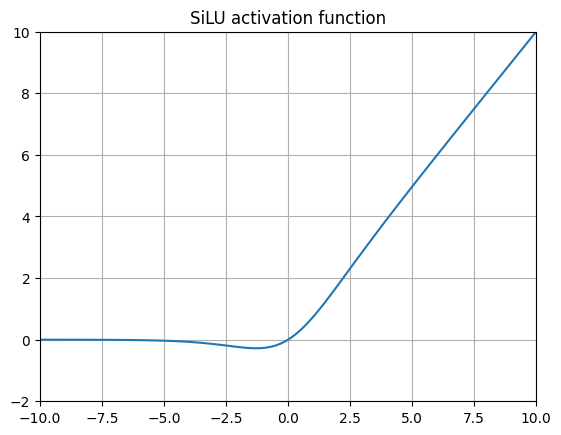
SiLU 是在 2016 年的原始 GELU 论文中引入的，后来其他研究人员对其进行了扩展。当我们用 Logistic CDF（ Sigmoid 函数）替换高斯 CDF 时，就得到了这个函数。后续研究人员使用强化学习进行 Atari 游戏测试 SiLU，发现性能有了显著提升。
Swish
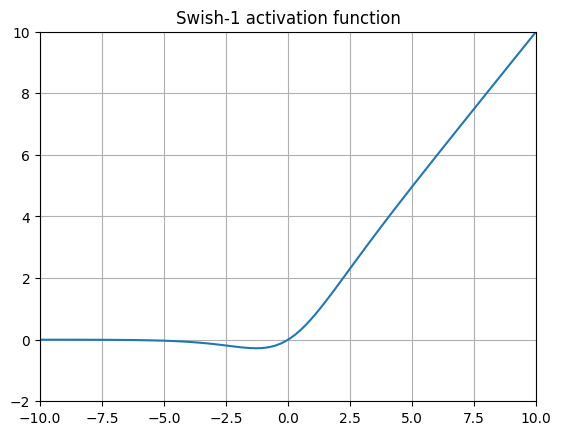
它看起来像耐克的标志，Swish 基本上是通过添加一个可训练的 \(\beta\) 参数对 SiLU 进行的小幅修改，这实际上增加了一个梯度项。许多实现中完全省略了这个 beta 参数（通常称为 Swish-1 ），这使得这个激活函数与 SiLU 完全相同！
SoLU (Softmax Linear Unit)
看到这里的模式了吗？这基本上是用 softmax 函数替换了 SiLU 中的 sigmoid 函数。这里的核心理念是旨在解释神经元的输出。这似乎会显著增加需要计算的指数运算次数和层输出的尺寸。作者报告说，模型的表现被限制在参数数量相当于 30-50%的等效模型的水平上。为了解决这个问题，作者声称，将每个 SoLU 用 LayerNorm 包装可以有效地解决这个问题，在性能和模型可解释性之间提供了一个合理的权衡。
GLU (Gated Linear Unit)
GLU 代表了 RNN 某些思想的延伸——即使用可学习的门控来控制流入后续层的信息，并在必要时丢弃信息。GLU 源自一篇（pre-transformer）2016 年的论文，该论文旨在开发用于语言建模的门控卷积网络（GCNs）。
原始论文的基本思想是对 \(x\) 进行线性变换，使用权重矩阵 \(V\) 和偏差 \(c\) \((xV +c)\) 。然后应用门控函数 \(sigmoid(xW + b)\) ，在受 RNN 门控启发的操作中，有效决定哪些信息传递到下一层或不传递。
GLU 的一个值得注意的近期应用是在 Evo “Striped Hyena” 模型中，用于长基因组序列规模建模。
尽管自 2016 年以来，使用卷积进行语言建模的想法已经逐渐被淘汰，但这篇论文中的 GLU 激活层以稍作修改的形式至今仍然存在……
GEGLU and SwiGLU
GeGLU 和 SwiGLU 是作为 GLU 的变体，由 Noam Shazeer 在 2020 年发表的一篇 5 页的单作者论文中开发的。 其基本思想是将 GLU 与 GELU 或 Swish 结合，用 GELU 门或 Swish 门来替代 sigmoid 门。
原始论文完全没有解释为什么这种方法能带来更好的性能指标，只是将其归因于“神的恩赐”，尽管思考激活函数的形状，我敢猜测性能可能与 Swish 和 GELU 中使用 \(sigmoid(x)\) 没有上界有关。
SwiGLU 早已被许多知名的 LLMs 采纳，包括 Google 的 PaLM 和 Meta 的 Llama2 ，使得这项技术在当前的语言建模领域几乎达到了最先进水平！
Smooth SwiGLU
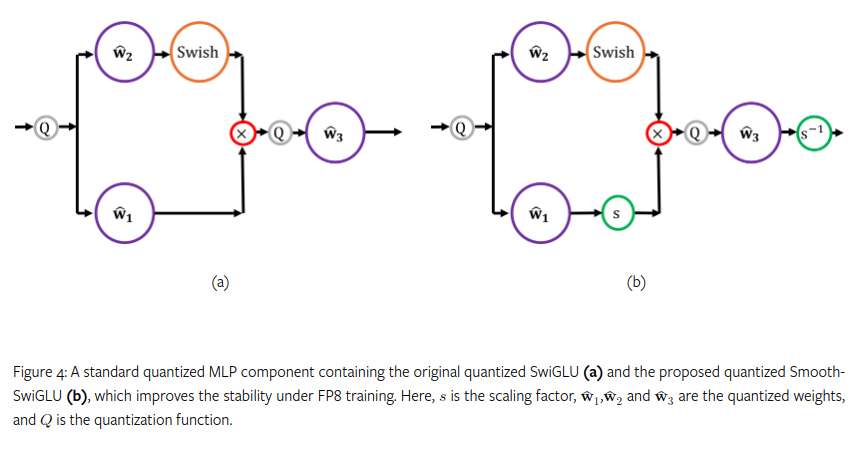
2024 年 9 月，英特尔 Habana 实验室在训练一个使用 SwiGLU 的 FP8 大型语言模型时，发现存在严重的不稳定性，该模型涉及 2 万亿个 token，最终问题被追溯到 SwiGLU 的使用。在处理到 2000 亿个 token 时，他们发现异常值会被放大。为了解决这个问题，他们开发了一种新的激活函数，称为 Smooth-SwiGLU。
结论
在回顾这些函数及其历史时，一个显而易见的是，尽管现在野外出现了许多令人望而生畏的缩写词，但 2016 年后的许多常用激活函数本质上都使用相同的“Swish”形状和 \(x * F_{cdf}(x)\) 函数。SiLU、Swish、GeLU 和 SoLU 都属于这一类。
这些方法比 ReLU 的计算成本要高得多。例如，FlashAttention-3 论文指出，一块 H100 SXM5 GPU 有 989 TFLOPs 的 F16 矩阵乘法能力，但对于指数函数（用于 Sigmoid 和 Softmax 计算）等特殊函数，只有 3.9 TFLOPs。 要从硬件中榨取真正的性能，需要复杂的异步调度来让深度学习发出嗡嗡声。
然而，不同团队在从 LLMs 中榨取每一分性能方面投入了大量资源，我这里提到的最后几种激活函数（SwiGLU 和 GEGLU）计算量非常大