引言与背景

FlashAttention的关键创新在于使用类似于在线Softmax的思想来对自注意力计算进行分块（tiling），从而能够融合整个多头注意力层的计算，而无需访问GPU全局内存来存储中间的logits和注意力分数

在深度学习中，Transformer模型的自注意力机制是计算密集型操作。传统实现需要在GPU全局内存中存储大量中间结果，这导致：

内存瓶颈：中间矩阵占用大量显存
I/O开销：频繁的全局内存访问降低效率
扩展性限制：难以处理超长序列
FlashAttention通过算法创新解决了这些问题。

Self-Atention

自注意力机制的计算可以总结为（为简化说明，忽略头数和批次维度，也省略注意力掩码和缩放因子 $\frac{1}{D}$ ）：

O = softmax (Q K^{T}) V

其中：

$Q, K, V, O$ 都是形状为 $(L, D)$ 的二维矩阵
$L$ 是序列长度
$D$ 是每个头的维度（头维度）
softmax应用于最后一个维度（列）
标准计算流程，传统方法将自注意力计算分解为几个阶段：

X = Q K^{T} A = softmax (X) O = A V

其中：

$X$ 矩阵称为预softmax logits
$A$ 矩阵称为注意力分数（attention score）
$O$ 矩阵是最终输出
内存问题:

这种分阶段计算需要在全局内存中物化（materialize） $X$ 和 $A$ 矩阵，导致显著的内存开销

对于经典算法如矩阵乘法，分块（tiling）用于确保片上内存不超过硬件限制。

矩阵乘法分块示例：

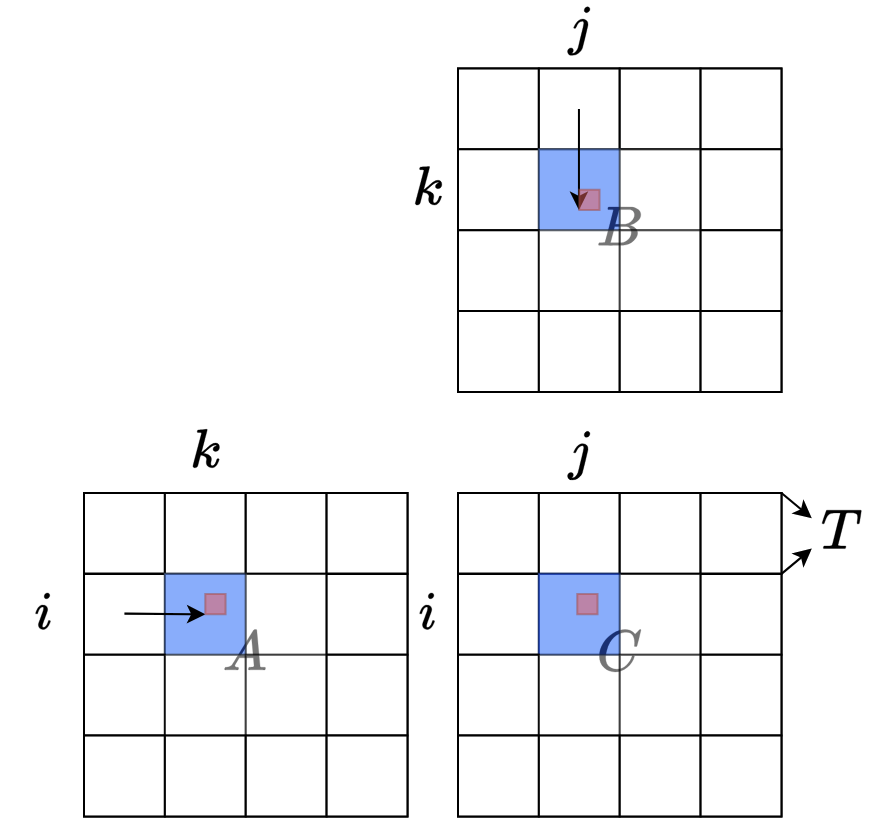
上图简要解释了如何对矩阵乘法 $C = A \times B$ 的输入和输出矩阵进行分块，矩阵被划分为 $T \times T$ 个块。对于每个输出块，我们从左到右扫描 $A$ 中的相关块，从上到下扫描 $B$ 中的相关块，并将值从全局内存加载到片上内存（蓝色部分，总体片上内存占用为 $O (T^{2})$ ）。对于分块的部分矩阵乘法，对于位置 $(i, j)$ ，我们从片上内存中加载块内所有 $k$ 的 $A [i, k]$ 和 $B [k, j]$ （红色部分），然后在片上内存中将 $A [i, k] \times B [k, j]$ 聚合到 $C [i, j]$ 。当一个块的计算完成后，我们将片上的 $C$ 块写回主内存，然后继续处理下一个块。实际应用中的分块要复杂得多，可以参考 A100 上矩阵乘法的 Cutlass 实现

然而，自注意力机制包含softmax算子，而softmax不具有直接的结合律，这使得无法像矩阵乘法那样简单地进行分块。

所以核心问题是：如何使softmax具有结合律特性？

(Safe)Softmax

标准softmax算子的通用公式为：

softmax ({x_{1}, \dots, x_{N}}) = (\frac{e ^{x_{i}}}{\sum _{j = 1}^{N} e ^{x_{j}}})_{i = 1}^{N}

可以注意到 $x_{i}$ 可能非常大，导致 $e^{x_{i}}$ 容易溢出。

为缓解这个问题，数学软件通常采用"安全"softmax技巧：

\frac{e ^{x_{i}}}{\sum _{j = 1}^{N} e ^{x_{j}}} = \frac{e ^{x_{i} - m}}{\sum _{j = 1}^{N} e ^{x_{j} - m}}

其中 $m = max_{j = 1}^{N} (x_{j})$ ，这样可以确保每个 $x_{i} - m \leq 0$ ，因为指数算子对负输入是精确的。

**算法：3-Pass safe Softmax
符号定义**：
${m_{i}}$ ： $max_{j = 1}^{i} (x_{j})$ ，初始值 $m_{0} = - \infty$ ${d_{i}}$ ： $\sum_{j = 1}^{i} e^{x_{j} - m_{N}}$ ，初始值 $d_{0} = 0$ ， $d_{N}$ 是安全softmax的分母
${a_{i}}$ ：最终的softmax值
算法主体：
** ** $for i = 1 to N do:$

这个算法需要迭代 $[1, N]$ 三次。在Transformer的自注意力上下文中， ${x_{i}}$ 是由 $Q K^{T}$ 计算的pre-softmax logits。

如果我们没有存储所有logits ${x_{i}}_{i = 1}^{N}$ （因为SRAM不够大），我们需要访问Q和K三次（以即时重新计算logits），这在I/O上是低效的。

Online Softmax

如果可以只用单个循环，就可以将全局内存访问次数从3次减少到1次。但我们无法在同一循环中融合前两个方程，因为第二个方程依赖于 $m_{N}$ ，而 $m_{N}$ 只有在第一个循环完成后才能确定。

可以创建另一个序列 $d_{i}^{'} := \sum_{j = 1}^{i} e^{x_{j} - m_{i}}$ 作为原始序列 $d_{i} := \sum_{j = 1}^{i} e^{x_{j} - m_{N}}$ 的替代。

这两个序列的第N项是相同的： $d_{N} = d_{N}^{'}$ ，因此我们可以安全地在方程(3)用 $d_{N}^{'}$ 替换 $d_{N}$ 。

可以找到 $d_{i}^{'}$ 和 $d_{i - 1}^{'}$ 之间的递归关系：

d_{i}^{'} = j = 1 \sum i e^{x_{j} - m_{i}} = (j = 1 \sum i - 1 e^{x_{j} - m_{i}}) + e^{x_{i} - m_{i}} = (j = 1 \sum i - 1 e^{x_{j} - m_{i - 1}}) e^{m_{i - 1} - m_{i}} + e^{x_{i} - m_{i}} = d_{i - 1}^{'} e^{m_{i - 1} - m_{i}} + e^{x_{i} - m_{i}}

这个递归形式只依赖于 $m_{i}$ 和 $m_{i - 1}$ ，我们可以在同一循环中一起计算 $m_{j}$ 和 $d_{j}^{'}$ 。

**算法：2-Pass online-Softmax
** $for i = 1 to N do:$

这是online-Softmax论文中提出的算法。

FlashAttention

能否将遍历次数减少到1次以最小化全局I/O？

对于softmax本身，答案是"否"。但在自注意力机制中，我们的最终目标不是注意力分数矩阵 $A$ ，而是输出矩阵 $O = A \times V$ 。我们能否为 $O$ 找到一遍递归形式？

让我们将自注意力计算的第 $k$ 行（所有行的计算是独立的，为简化说明只解释一行的计算）表述为递归算法：

**算法：Multi-pass Self-Attention
符号定义**：
$Q [k, :]$ ：Q矩阵的第 $k$ 行向量
$K^{T} [:, i]$ ： $K^{T}$ 矩阵的第 $i$ 列向量
$O [k, :]$ ：输出O矩阵的第 $k$ 行
$V [i, :]$ ： $V$ 矩阵的第 $i$ 行
${o_{i}}$ ： $\sum_{j = 1}^{i} a_{j} V [j, :]$ ，存储部分聚合结果 $A [k, : i] \times V [: i, :]$ 的行向量

算法主体：
**计算注意力分数
** $for i = 1 to N do:$

让我们用方程5中的定义替换方程4中的 $a_{i}$ ：

o_{i} := j = 1 \sum i \frac{e ^{x_{j} - m_{N}}}{d _{N}^{'}} V [j, :]

可以看出，这仍然依赖于 $m_{N}$ 和 $d_{N}$ ，它们在前一个循环完成之前无法确定。

但可以再次使用上面介绍的"替代"技巧，创建一个替代序列 $o^{'}$ ：

o_{i}^{'} := j = 1 \sum i \frac{e ^{x_{j} - m_{i}}}{d _{i}^{'}} V [j, :]

$o$ 和 $o^{'}$ 的第 $N$ 个元素是相同的：

o_{N}^{'} = o_{N}

同样，可以找到 $o_{i}^{'}$ 和 $o_{i - 1}^{'}$ 之间的递归关系：

o_{i}^{'} = j = 1 \sum i \frac{e ^{x_{j} - m_{i}}}{d _{i}^{'}} V [j, :] = (j = 1 \sum i - 1 \frac{e ^{x_{j} - m_{i}}}{d _{i}^{'}} V [j, :]) + \frac{e ^{x_{i} - m_{i}}}{d _{i}^{'}} V [i, :] = (j = 1 \sum i - 1 \frac{e ^{x_{j} - m_{i - 1}}}{d _{i - 1}^{'}} \cdot \frac{e ^{x_{j} - m_{i}}}{e ^{x_{j} - m_{i - 1}}} \cdot \frac{d _{i - 1}^{'}}{d _{i}^{'}} V [j, :]) + \frac{e ^{x_{i} - m_{i}}}{d _{i}^{'}} V [i, :] = (j = 1 \sum i - 1 \frac{e ^{x_{j} - m_{i - 1}}}{d _{i - 1}^{'}} V [j, :]) \frac{d _{i - 1}^{'} e ^{m_{i - 1} - m_{i}}}{d _{i}^{'}} + \frac{e ^{x_{i} - m_{i}}}{d _{i}^{'}} V [i, :] = o_{i - 1}^{'} \frac{d _{i - 1}^{'} e ^{m_{i - 1} - m_{i}}}{d _{i}^{'}} + \frac{e ^{x_{i} - m_{i}}}{d _{i}^{'}} V [i, :]

这个递归关系只依赖于 $d_{i}^{'}$ 、 $d_{i - 1}^{'}$ 、 $m_{i}$ 、 $m_{i - 1}$ 和 $x_{i}$ ，因此我们可以在单个循环中融合自注意力的所有计算！

**算法：FlashAttention（单遍）
** $for i = 1 to N do:$

关键优势：状态 $x_{i}$ 、 $m_{i}$ 、 $d_{i}^{'}$ 和 $o_{i}^{'}$ 的内存占用很小，可以轻松放入GPU共享内存。

因为这个算法中的所有操作都是结合的（associative），所以它与分块兼容。如果我们逐块计算状态，算法可以表示如下：

**算法：FlashAttention（分块版本）
新符号定义**：

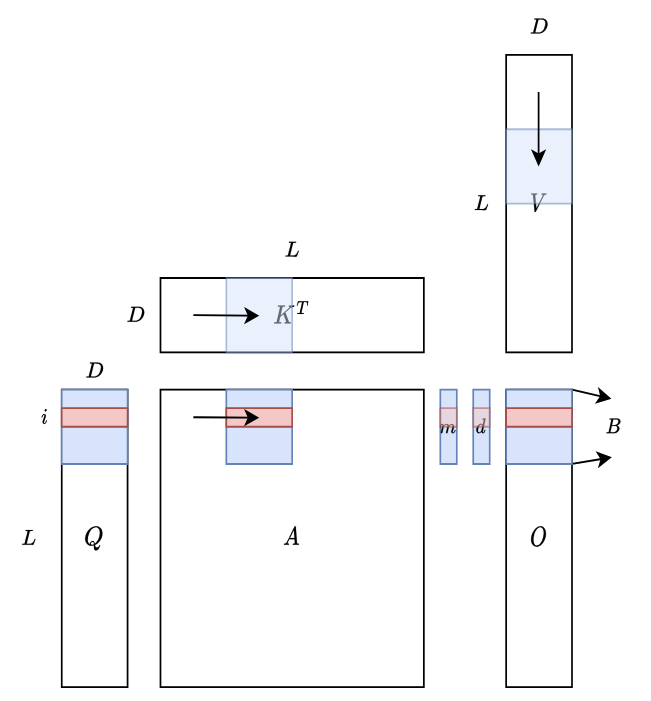
上图说明了 FlashAttention 如何在硬件上进行计算。蓝色块代表驻留在 SRAM 中的块，而红色块对应第 $i$ 行。 $L$ 表示序列长度，可能非常大（例如 16k）， $D$ 表示头维度，在 Transformer 中通常较小（例如 GPT3 中为 128）， $B$ 是可以控制的块大小。
值得注意的是，整体 SRAM 内存占用仅取决于 $B$ 和 $D$ ，与 $L$ 无关。因此，该算法可以扩展到长上下文而不会遇到内存问题（GPU 共享内存很小，H100 架构中每个 SM 为 228kb）。在计算过程中，我们从左到右扫描 $K^{T}$ 和 $A$ 的块，从上到下扫描 $V$ 的块，并相应地更新 $m$ 、 $d$ 和 $O$ 的状态。

Reference

🔖 https://courses.cs.washington.edu/courses/cse599m/23sp/notes/flashattn.pdf

#

!

Flash-Attention