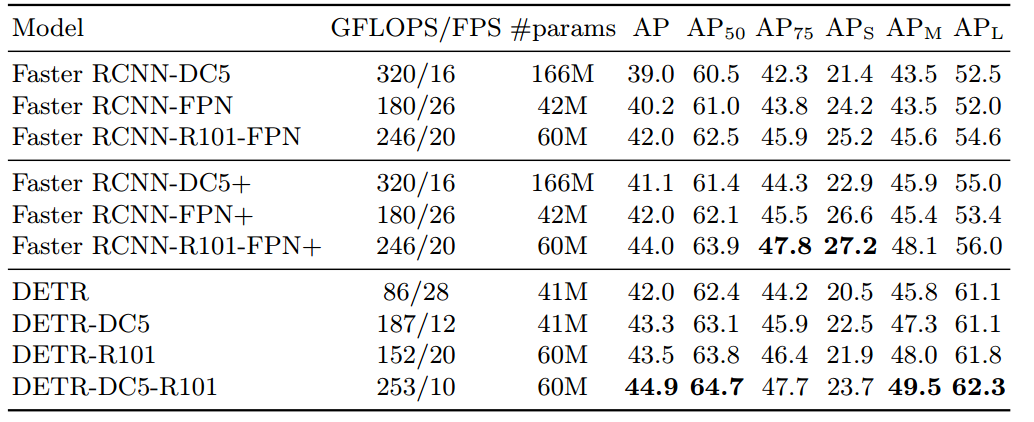
原理分析

网络架构:

本文的任务是Object detection，用到的工具是Transformers，特点是End-to-end。

目标检测的任务是要去预测一系列的Bounding Box的坐标以及Label，现代大多数检测器通过定义一些proposal，anchor或者windows，把问题构建成为一个分类和回归问题来间接地完成这个任务。文章所做的工作，就是将transformers运用到了object detection领域，取代了现在的模型需要手工设计的工作，并且取得了不错的结果。在object detection上DETR准确率和运行时间上和Faster RCNN相当；将模型 generalize 到 panoptic segmentation 任务上，DETR表现甚至还超过了其他的baseline。DETR第一个使用End to End的方式解决检测问题，解决的方法是把检测问题视作是一个set prediction problem，如下图所示。

网络的主要组成是CNN和Transformer，Transformer借助self-attention机制，可以显式地对一个序列中的所有elements两两之间的interactions进行建模，使得这类transformer的结构非常适合带约束的set prediction的问题。DETR的特点是：一次预测，端到端训练，set loss function和二分匹配。

文章的主要有两个关键的部分。

第一个是用transformer的encoder-decoder架构一次性生成 $N$ 个box prediction。其中 $N$ 是一个事先设定的、比远远大于image中object个数的一个整数，文章中设定$N=100$。
第二个是设计了bipartite matching loss，基于预测的boxex和ground truth boxes的二分图匹配计算loss的大小，从而使得预测的box的位置和类别更接近于ground truth。
DETR整体结构可以分为四个部分：backbone，encoder，decoder和FFN，如下图所示，以下分别解释这四个部分：

backbone

CNN backbone处理 $x_{img}∈B×3×H_0×W_0$ 维的图像，把它转换为$f\in R^{B\times C\times H\times W}$ 维的feature map（一般来说或$C=2048$或256,$H=\frac{H_0}{32},W=\frac{W_0}{32}$），backbone只做这一件事。

encoder

encoder的输入是$f\in R^{B\times C\times H\times W}$维的feature map，接下来依次进行以下过程：

位置编码

进行完位置编码以后根据paper中的图片会有个相加的过程，如下图问号处所示。很多读者有疑问的地方是：论文图中相加的2个张量，一个是input embedding，另一个是位置编码维度看上去不一致，是怎么相加的？后面会解答。

原版Transformer和Vision Transformer的Positional Encoding的表达式为：

\[ \begin{align}PE_{(pos, 2i)} = sin(pos/10000^{2i/d}) \\ PE_{(pos, 2i+1)} = cos(pos/10000^{2i/d}) \end{align}\tag{1} \]

式中， $d$ 就是这个 $d\times HW$ 维的feature map的第一维， $pos\in [1,HW]$。表示token在sequence中的位置，sequence的长度是 $HW$ ，例如第一个token 的 $pos=0$ 。

$i$，或者准确意义上是 $2i$ 和 $2i+1$ 表示了Positional Encoding的维度，$i$ 的取值范围是： $\left[ 0,\ldots ,{{{d}}}/{2}\; \right)$。所以当 $pos$ 为1时，对应的Positional Encoding可以写成：

\[ PE\left( 1 \right)=\left[ \sin \left( {1}/{{{10000}^{{0}/{256}\;}}}\; \right),\cos \left( {1}/{{{10000}^{{0}/{256}\;}}}\; \right),\sin \left( {1}/{{{10000}^{{2}/{256}\;}}}\; \right),\cos \left( {1}/{{{10000}^{{2}/{256}\;}}}\; \right),\ldots \right] \]

式中， $d=256$。

第一点不同的是，原版Transformer只考虑 $x$ 方向的位置编码，但是DETR考虑了 $xy$ 方向的位置编码，因为图像特征是2-D特征。采用的依然是 sin cos 模式，但是需要考虑 $xy$ 两个方向。不是类似vision transoformer做法简单的将其拉伸为 $d\times HW$ ，然后从$[1, HW]$ 进行长度为256的位置编码，而是考虑了 $xy$ 方向同时编码，每个方向各编码128维向量，这种编码方式更符合图像特点。
另一点不同的是，原版Transformer只在Encoder之前使用了Positional Encoding，而且是在输入上进行Positional Encoding，再把输入经过transformation matrix变为Query，Key和Value这几个张量。但是DETR在Encoder的每一个Multi-head Self-attention之前都使用了Positional Encoding，且只对Query和Key使用了Positional Encoding，即：只把维度为$(HW,B,256)$ 维的位置编码与维度为$(HW,B,256)$ 维的Query和Key相加，而不与Value相加。
如下图所示为DETR的Transformer的详细结构和原版Transformer的结构

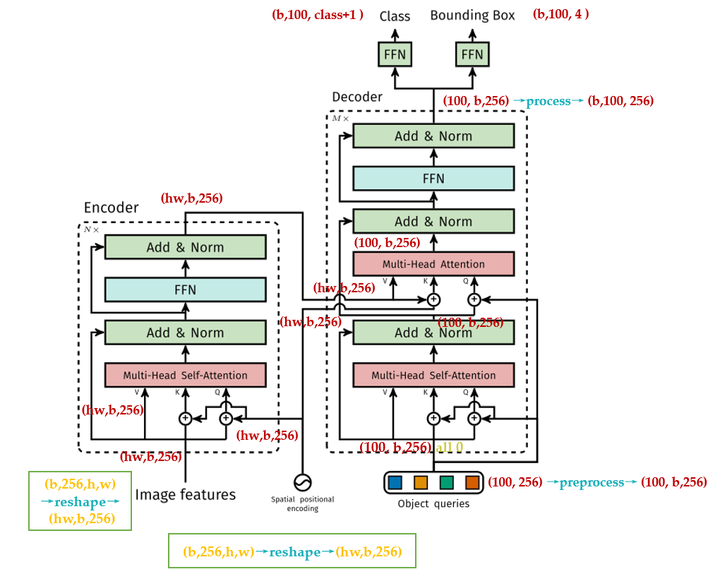
可以发现，除了Positional Encoding设置的不一样外，Encoder其他的结构是一致的。每个Encoder Layer包含一个multi-head self-attention 的module和一个前馈网络Feed Forward Network。

Encoder最终输出的是$(H\cdot W,b,256)$维的编码矩阵Embedding，按照原版Transformer的做法，把这个东西给Decoder。

总结下和原始transformer编码器不同的地方：

输入编码器的位置编码需要考虑2-D空间位置。
位置编码向量需要加入到每个Encoder Layer中。
在编码器内部位置编码Positional Encoding仅仅作用于Query和Key，即只与Query和Key相加，Value不做任何处理。

Decoder

DETR的Decoder和原版Transformer的decoder是不太一样的，如上面两图对比所示。

先回忆下原版Transformer，decoder的最后一个框：output probability，代表一次只产生一个单词的softmax，根据这个softmax得到这个单词的预测结果。这个过程我们表达为：predicts the output sequence one element at a time。

不同的是，DETR的Transformer Decoder是一次性处理全部的object queries，即一次性输出全部的predictions；而不像原始的Transformer是auto-regressive的，从左到右一个词一个词地输出。这个过程我们表达为：decodes the N objects in parallel at each decoder layer。

DETR的Decoder主要有两个输入：

Transformer Encoder输出的Embedding与 position encoding 之和。
Object queries。
其中，Embedding就是上文提到的$(H\cdot W,b,256)$ 的编码矩阵。这里着重讲一下Object queries。

Object queries是一个维度为 $(100,b,256)$ 维的张量，数值类型是nn.Embedding，说明这个张量是可以学习的，即：我们的Object queries是可学习的。Object queries矩阵内部通过学习建模了100个物体之间的全局关系，例如房间里面的桌子旁边(A类)一般是放椅子(B类)，而不会是放一头大象(C类)，那么在推理时候就可以利用该全局注意力更好的进行解码预测输出。

Decoder的输入一开始也初始化成维度为 $(100,b,256) $维的全部元素都为0的张量，和Object queries加在一起之后充当第1个multi-head self-attention的Query和Key。第一个multi-head self-attention的Value为Decoder的输入，也就是全0的张量。

到了每个Decoder的第2个multi-head self-attention，它的Key和Value来自Encoder的输出张量，维度为 $(hw,b,256)$，其中Key值还进行位置编码。Query值一部分来自第1个Add and Norm的输出，维度为 $(100,b,256)$ 的张量，另一部分来自Object queries，充当可学习的位置编码。所以，第2个multi-head self-attention的Key和Value的维度为$(hw,b,256)$ ，而Query的维度为$(100,b,256)$。

每个Decoder的输出维度为 $(1,b,100,256)$ ，送入后面的前馈网络。

到这里你会发现：Object queries充当的其实是位置编码的作用，只不过它是可以学习的位置编码，所以，我们对Encoder和Decoder的每个self-attention的Query和Key的位置编码做个归纳，如下图所示，Value没有位置编码：

损失函数

得到了Decoder的输出以后，如前文所述，应该是输出维度为$(b,100,256)$的张量。接下来要送入2个前馈网络FFN得到class和Bounding Box。它们会得到 $N=100$ 个预测目标，包含类别和Bounding Box，当然这个100肯定是大于图中的目标总数的。如果不够100，则采用背景填充，计算loss时候回归分支分支仅仅计算有物体位置，背景集合忽略。所以，DETR输出张量的维度为输出的张量的维度是$(b,100,\color{crimson}{\text{class}+1})$和$(b,100,\color{purple}{4})$。对应COCO数据集来说， class+1=92 ， 4 指的是每个预测目标归一化的$(c_x,c_y,w,h)$。归一化就是除以图片宽高进行归一化。

到这里我们了解了DETR的网络架构，我们发现，它输出的张量的维度是 分类分支：$(b,100,\color{crimson}{\text{class}+1})$ 和回归分支：$(b,100,\color{purple}{4})$，其中，前者是指100个预测框的类型，后者是指100个预测框的Bounding Box，但是读者可能会有疑问：预测框和真值是怎么一一对应的？换句话说：你怎么知道第47个预测框对应图片里的狗，第88个预测框对应图片里的车？等等。

我们下面就来聊聊这个问题。

set prediction

相比Faster R-CNN等做法，DETR最大特点是将目标检测问题转化为无序集合预测问题(set prediction)。论文中特意指出Faster R-CNN这种设置一大堆anchor，然后基于anchor进行分类和回归其实属于代理做法即不是最直接做法，目标检测任务就是输出无序集合，而Faster R-CNN等算法通过各种操作，并结合复杂后处理最终才得到无序集合属于绕路了，而DETR就比较纯粹了。现在核心问题来了：输出的 $(b,100)$个检测结果是无序的，如何和 GT Bounding Box 计算loss？这就需要用到经典的双边匹配算法了，也就是常说的匈牙利算法，该算法广泛应用于最优分配问题。

一幅图片，我们把第 $i$ 个物体的真值表达为 $y_i=(c_i,b_i)$，其中， $c_i$ 表示它的 class ， $b_i$ 表示它的 Bounding Box 。我们定义 $\hat y = \{\hat y_i\}_{i=1}^{N}$ 为网络输出的 $N$ 个预测值。

假设我们已经了解了什么是匈牙利算法(先假装了解了)，对于第 $i$ 个 GT ，$\sigma(i)$ 为匈牙利算法得到的与$GT_i$ 对应的prediction的索引。我举个栗子，比如 $i=3,\sigma(i)=18$ ，意思就是：与第3个真值对应的预测值是第18个。

那我能根据匈牙利算法，找到与每个真值对应的预测值是哪个，那究竟是如何找到呢？

\[ \begin{equation} \hat{\sigma} = \arg\min_{\sigma\in\Sigma_N} \sum_{i}^{N} L_{match}(y_i, \hat y_{\sigma(i)}), \end{equation}\tag{3} \]

我们看看这个表达式是甚么意思，对于某一个真值 $y_i$ ，假设我们已经找到这个真值对应的预测值 $\hat y_{\sigma(i)}$ ，这里的$ Σ_N$ 是所有可能的排列，代表从真值索引到预测值索引的所有的映射，然后用 $L_{match}$ 最小化 $y_i$ 和 $\hat y_{\sigma(i)}$ 的距离。这个 $L_{match}$ 具体是：

\[ -\mathbb{1}_{\left\{ c_i\neq\varnothing \right\}}\hat p_{\sigma(i)}(c_i) + \mathbb{1}_{\left\{ c_i\neq\varnothing \right\}} L_{box}({b_{i}, \hat b_{\sigma(i)}}) \tag{4} \]

意思是：假设当前从真值索引到预测值索引的所有的映射为 $\sigma$ ，对于图片中的每个真值 $i$ ，先找到对应的预测值 $\sigma(i)$ ，再看看分类网络的结果 $\hat p_{\sigma(i)}(c_i) $ ，取反作为 $L_{match}$ 的第1部分。再计算回归网络的结果 $\hat b_{\sigma(i)}$ 与真值的 Bounding Box 的差异，即 $L_{box}({b_{i}, \hat b_{\sigma(i)}})$ ，作为 $L_{match}$ 的第2部分。

所以，可以使得 $L_{match}$ 最小的排列 $\hat\sigma$ 就是我们要找的排列，即：对于图片中的每个真值 $i$ 来讲， $\hat\sigma(i)$ 就是这个真值所对应的预测值的索引。

请读者细品这个寻找匹配的过程，这就是匈牙利算法的过程。是不是与Anchor或Proposal有异曲同工的地方，只是此时我们找的是一对一匹配。

接下来就是使用上一步得到的排列 $\hat\sigma$ ，计算匈牙利损失：

\[ L_{\text{Hungarian}}({y, \hat y}) = \sum_{i=1}^N \left[-\log \hat p_{\hat{\sigma}(i)}(c_{i}) + \mathbb{1}_{\left\{ c_i\neq\varnothing \right\}} \ L_{box}{(b_{i}, \hat b_{\hat{\sigma}(i)}})\right] \tag{5} \]

式中的$L_{box}$ 具体为：

\[ L_{box}{(b_{i}, \hat b_{\hat{\sigma}(i)}}) = \lambda_{\rm iou}L_{iou}({b_{i}, \hat b_{\sigma(i)}})+ \lambda_{\rm L1}||b_{i}- \hat b_{\sigma(i)}||_1 ,\; where \;\lambda_{\rm iou}, \lambda_{\rm L1}\in R \tag{6} \]

最常用的 $L_1 \;loss$ 对于大小 Bounding Box 会有不同的标度，即使它们的相对误差是相似的。为了缓解这个问题，作者使用了 $L_1 \;loss$ 和广义IoU损耗 $L_{iou}$ 的线性组合，它是比例不变的。

Hungarian意思就是匈牙利，也就是前面的 $L_{match}$，上述意思是需要计算 $M$ 个 GTBounding Box 和 $N$ 个输预测出集合两两之间的广义距离，距离越近表示越可能是最优匹配关系，也就是两者最密切。广义距离的计算考虑了分类分支和回归分支。

最后，再概括一下DETR的End-to-End的原理，前面那么多段话就是为了讲明白这个事情，如果你对前面的论述还存在疑问的话，把下面一直到Experiments之前的这段话看懂就能解决你的困惑。

DETR是怎么训练的？

训练集里面的任何一张图片，假设第1张图片，我们通过模型产生100个预测框 PredictBounding Box ，假设这张图片有只3个 GTBounding Box ，它们分别是 $\color{orange}{\text{Car}},\color{green}{\text{Dog}},\color{darkturquoise}{\text{Horse}}$ 。

\[ (\text{label}_{\color{orange}{\text{Car}}}=3,\text{label}_{\color{green}{\text{Dog}}}=24,\text{label}_{\color{orange}{\color{darkturquoise}{\text{Horse}}}}=75)\\ \]

问题是：我怎么知道这100个预测框哪个是对应 Car ，哪个是对应 Dog ，哪个是对应 Horse ？

我们建立一个 (100,3) 的矩阵，矩阵里面的元素就是 (4) 式的计算结果，举个例子：比如左上角的 (1,1) 号元素的含义是：第1个预测框对应 $\color{orange}{\text{Car}}(\text{label}=3)$ 的情况下的 $L_{match}$ 值。我们用**scipy.optimize** 这个库中的 **linear_sum_assignment **函数找到最优的匹配，这个过程我们称之为："匈牙利算法 (Hungarian Algorithm)"。

假设**linear_sum_assignment**做完以后的结果是：第 23 个预测框对应 Car ，第 44 个预测框对应 Dog ，第 95 个预测框对应 Horse 。

现在把第 23,44,95 个预测框挑出来，按照 (5) 式计算Loss，得到这个图片的Loss。

把所有的图片按照这个模式去训练模型。

训练完以后怎么用？

训练完以后，你的模型学习到了一种能力，即：模型产生的100个预测框，它知道某个预测框该对应什么 Object ，比如，模型学习到：第1个 PredictBounding Box 对应 Car(label=3) ，第2个 PredictBounding Box 对应 Bus(label=16) ，第3个 PredictBounding Box 对应 Sky(label=21) ，第4个 PredictBounding Box 对应 Dog(label=24) ，第5个 PredictBounding Box 对应 Horse(label=75) ，第6-100个 PredictBounding Box 对应 ∅(label=92) ，等等。

以上只是我举的一个例子，意思是说：模型知道了自己的100个预测框每个该做什么事情，即：每个框该预测什么样的 Object 。

为什么训练完以后，模型学习到了一种能力，即：模型产生的100个预测框，它知道某个预测框该对应什么 Object ？

还记得前面说的Object queries吗？它是一个维度为$(100,b,256)$ 维的张量，初始时元素全为 0 。实现方式是nn.Embedding(num_queries, hidden_dim)，这里num_queries=100，hidden_dim=256，它是可训练的。这里的 $b$ 指的是batch size，我们考虑单张图片，所以假设Object queries是一个维度为 (100,256) 维的张量。我们训练完模型以后，这个张量已经训练完了，那此时的Object queries究竟代表什么？

我们把此时的Object queries看成100个格子，每个格子是个256维的向量。训练完以后，这100个格子里面注入了不同 Object 的位置信息和类别信息。比如第1个格子里面的这个256维的向量代表着 Car 这种 Object 的位置信息，这种信息是通过训练，考虑了所有图片的某个位置附近的 Car 编码特征，属于和位置有关的全局 Car 统计信息。

测试时，假设图片中有 Car,Dog,Horse 三种物体，该图片会输入到编码器中进行特征编码，假设特征没有丢失，Decoder的Key和Value就是编码器输出的编码向量，而Query就是Object queries，就是我们的100个格子。

Query可以视作代表不同 Object 的信息，而Key和Value可以视作代表图像的全局信息。

现在通过注意力模块将Query和Key计算，然后加权Value得到解码器输出。对于第1个格子的Query会和Key中的所有向量进行计算，目的是查找某个位置附近有没有 Car ，如果有那么该特征就会加权输出，对于第3个格子的Query会和Key中的所有向量进行计算，目的是查找某个位置附近有没有 Sky ，很遗憾，这个没有，所以输出的信息里面没有 Sky 。

整个过程计算完成后就可以把编码向量中的 Car,Dog,Horse 的编码嵌入信息提取出来，然后后面接 $FFN$ 进行分类和回归就比较容易，因为特征已经对齐了。

发现了吗？Object queries在训练过程中对于 $N$ 个格子会压缩入对应的和位置和类别相关的统计信息，在测试阶段就可以利用该Query去和某个图像的编码特征Key，Value计算，若图片中刚好有Query想找的特征，比如 Car ，则这个特征就能提取出来，最后通过2个 FFN 进行分类和回归。所以前面才会说Object queries作用非常类似Faster R-CNN中的anchor，这个anchor是可学习的，由于维度比较高，故可以表征的东西丰富，当然维度越高，训练时长就会越长。

这就是DETR的End-to-End的原理，可以简单归结为上面的几段话，你读懂了上面的话，也就明白了DETR以及End-to-End的Detection模型原理。

伪代码

下面是论文中给出的简化代码，可以直接跑，只是精度会差两个点。

import torch
from torch import nn
from torchvision.models import resnet50

class DETR(nn.Module):
    def __init__(self, num_classes, hidden_dim, nheads,
        num_encoder_layers, num_decoder_layers):
        super().__init__()
        # We take only convolutional layers from ResNet-50 model
        self.backbone = nn.Sequential(*list(resnet50(pretrained=True).children())[:-2])
        self.conv = nn.Conv2d(2048, hidden_dim, 1) # 1×1卷积层将2048维特征降到256维
        self.transformer = nn.Transformer(hidden_dim, nheads, num_encoder_layers, num_decoder_layers)
        self.linear_class = nn.Linear(hidden_dim, num_classes + 1) # 类别FFN
        self.linear_bbox = nn.Linear(hidden_dim, 4)                # 回归FFN
        self.query_pos = nn.Parameter(torch.rand(100, hidden_dim)) # object query
        # 下面两个是位置编码
        self.row_embed = nn.Parameter(torch.rand(50, hidden_dim // 2))
        self.col_embed = nn.Parameter(torch.rand(50, hidden_dim // 2))

    def forward(self, inputs):
        x = self.backbone(inputs)
        h = self.conv(x)
        H, W = h.shape[-2:]
        pos = torch.cat([self.col_embed[:W].unsqueeze(0).repeat(H, 1, 1),
                         self.row_embed[:H].unsqueeze(1).repeat(1, W, 1),
                         ], dim=-1).flatten(0, 1).unsqueeze(1) # 位置编码

        h = self.transformer(pos + h.flatten(2).permute(2, 0, 1),self.query_pos.unsqueeze(1))
        return self.linear_class(h), self.linear_bbox(h).sigmoid()


detr = DETR(num_classes=91, hidden_dim=256, nheads=8, num_encoder_layers=6, num_decoder_layers=6)
detr.eval()
inputs = torch.randn(1, 3, 800, 1200)
logits, bboxes = detr(inputs)

Experiments

1. 性能对比：