MoE(Mixture-of-Experts) 概述

Dec 29, 2024
84 views
Deep Learning
# transformer

简短总结

混合专家模型 (MoEs):

  • 与稠密模型相比， 预训练速度更快
  • 与具有相同参数数量的模型相比，具有更快的 推理速度
  • 需要 大量显存，因为所有专家系统都需要加载到内存中
  • 在 微调方面存在诸多挑战，但 近期的研究 表明，对混合专家模型进行 指令调优具有很大的潜力。

什么是混合专家模型？

模型规模是提升模型性能的关键因素之一。在有限的计算资源预算下，用更少的训练步数训练一个更大的模型，往往比用更多的步数训练一个较小的模型效果更佳。

混合专家模型 (MoE) 的一个显著优势是它们能够在远少于稠密模型所需的计算资源下进行有效的预训练。这意味着在相同的计算预算条件下，您可以显著扩大模型或数据集的规模。特别是在预训练阶段，与稠密模型相比，混合专家模型通常能够更快地达到相同的质量水平。

那么，究竟什么是一个混合专家模型 (MoE) 呢？作为一种基于 Transformer 架构的模型，混合专家模型主要由两个关键部分组成:

  • 稀疏 MoE 层: 这些层代替了传统 Transformer 模型中的前馈网络 (FFN) 层。MoE 层包含若干“专家”(例如 8 个)，每个专家本身是一个独立的神经网络。在实际应用中，这些专家通常是前馈网络 (FFN)，但它们也可以是更复杂的网络结构，甚至可以是 MoE 层本身，从而形成层级式的 MoE 结构。
  • 门控网络或路由: 这个部分用于决定哪些令牌 (token) 被发送到哪个专家。例如，在下图中，“More”这个令牌可能被发送到第二个专家，而“Parameters”这个令牌被发送到第一个专家。有时，一个令牌甚至可以被发送到多个专家。令牌的路由方式是 MoE 使用中的一个关键点，因为路由器由学习的参数组成，并且与网络的其他部分一同进行预训练。
    总结来说，在混合专家模型 (MoE) 中，我们将传统 Transformer 模型中的每个前馈网络 (FFN) 层替换为 MoE 层，其中 MoE 层由两个核心部分组成: 一个门控网络和若干数量的专家。

尽管混合专家模型 (MoE) 提供了若干显著优势，例如更高效的预训练和与稠密模型相比更快的推理速度，但它们也伴随着一些挑战:

  • 训练挑战: 虽然 MoE 能够实现更高效的计算预训练，但它们在微调阶段往往面临泛化能力不足的问题，长期以来易于引发过拟合现象。
  • 推理挑战: MoE 模型虽然可能拥有大量参数，但在推理过程中只使用其中的一部分，这使得它们的推理速度快于具有相同数量参数的稠密模型。然而，这种模型需要将所有参数加载到内存中，因此对内存的需求非常高。以 Mixtral 8x7B 这样的 MoE 为例，需要足够的 VRAM 来容纳一个 47B 参数的稠密模型。之所以是 47B 而不是 8 x 7B = 56B，是因为在 MoE 模型中，只有 FFN 层被视为独立的专家，而模型的其他参数是共享的。此外，假设每个令牌只使用两个专家，那么推理速度 (以 FLOPs 计算) 类似于使用 12B 模型 (而不是 14B 模型)，因为虽然它进行了 2x7B 的矩阵乘法计算，但某些层是共享的。
    了解了 MoE 的基本概念后，让我们进一步探索推动这类模型发展的研究。

混合专家模型简史

Adaptive mixtures of local experts

  • 期刊/会议：Neural Computation (1991)
  • 论文链接：https://readpaper.com/paper/2150884987
  • 代表性作者：Michael Jordan, Geoffrey Hinton
    这是大多数MoE论文都引用的最早的一篇文章，发表于1991年，作者中有两个大家熟知的大佬：Michael Jordan 和 Geoffrey Hinton。虽然是30年前的论文，但是读起来还是很流畅，没有什么“距离感”，建议读一读。

Main Idea：

提出了一种新的监督学习过程，一个系统中包含多个分开的网络，每个网络去处理全部训练样本的一个子集。这种方式可以看做是把多层网络进行了模块化的转换。

假设我们已经知道数据集中存在一些天然的子集（比如来自不同的domain，不同的topic），那么用单个模型去学习，就会受到很多干扰（interference），导致学习很慢、泛化困难。这时，我们可以使用多个模型（即专家，expert）去学习，使用一个门网络（gating network）来决定每个数据应该被哪个模型去训练，这样就可以减轻不同类型样本之间的干扰。

其实这种做法，也不是该论文第一次提出的，更早就有人提出过类似的方法。对于一个样本 \(c\)，第 \(i\) 个 expert 的输出为 \(o_i^c\)，理想的输出是 \(d^c\)，那么损失函数就这么计算：

\[ E^c=||d^c-\sum_ip_i^co_i^c||^2 \]

其中 \(p_i^c\) 是 gating network 分配给每个 expert 的权重，相当于多个 expert 齐心协力来得到当前样本 \(c\) 的输出。

这是一个很自然的设计方式，但是存在一个问题——不同的 expert 之间的互相影响会非常大，一个expert的参数改变了，其他的都会跟着改变，即所谓牵一发而动全身。这样的设计，最终的结果就是一个样本会使用很多的expert来处理。于是，这篇文章设计了一种新的方式，调整了一下loss的设计，来鼓励不同的expert之间进行竞争：

\[ E^c=p_i^c||d^c-\sum_io_i^c||^2 \]

就是让不同的 expert 单独计算 loss，然后在加权求和得到总体的 loss。这样的话，每个专家，都有独立判断的能力，而不用依靠其他的 expert 来一起得到预测结果。下面是一个示意图：

image

MoE

在这种设计下，我们将 experts 和 gating network 一起进行训练，最终的系统就会倾向于让一个 expert 去处理一个样本。

上面的两个 loss function，其实长得非常像，但是一个是鼓励合作，一个是鼓励竞争。这一点还是挺启发人的。

论文还提到另外一个很启发人的 trick，就是上面那个损失函数，作者在实际做实验的时候，用了一个变体，使得效果更好：

\[ Original:\ \ E^c=p_i^c||d^c-\sum_io_i^c||^2 \\ Modified: \ \ E^c=-log\sum_ip_i^ce^{-\frac{1}{2}||d^c-o_i^c||^2} \]

对比一下可以看出，在计算每个 expert 的损失之后，先把它给指数化了再进行加权求和，最后取了log。这也是一个我们在论文中经常见到的技巧。这样做有什么好处呢，我们可以对比一下二者在反向传播的时候有什么样的效果，使用 \(E^c\) 对 第 \(i\) 个 expert 的输出求导，分别得到：

\[ \begin{aligned}\text{original derivative: }&\ \ \ \ \frac{\partial {E}^{c}}{\partial {\mathbf{o}}_{i}^{c}} = - 2{p}_{i}^{c}\left( {{\mathbf{d}}^{c} - {\mathbf{o}}_{i}^{c}}\right)\\ \text{new derivative }: &\ \ \ \ \frac{\partial {E}^{c}}{\partial {\mathbf{o}}_{i}^{c}} = - \left\lbrack \frac{{p}_{i}^{c}{e}^{-\frac{1}{2}{\begin{Vmatrix}{\mathbf{d}}^{c} - {\mathbf{o}}_{i}^{c}\end{Vmatrix}}^{2}}}{\mathop{\sum }\limits_{j}{p}_{j}^{c}{e}^{-\frac{1}{2}{\begin{Vmatrix}{\mathbf{d}}^{c} - {\mathbf{o}}_{j}^{c}\end{Vmatrix}}^{2}}}\right\rbrack \left( {{\mathbf{d}}^{c} - {\mathbf{o}}_{i}^{c}}\right) \end{aligned} \]

可以看到，前者的导数，只会跟当前 expert 有关，但后者则还考虑其他 experts 跟当前 sample \(c\) 的匹配程度。换句话说，如果当前 sample 跟其他的 experts 也比较匹配，那么 \(E^c\) 对 第 \(i\) 个 expert 的输出的导数也会相对更小一些。（其实看这个公式，跟我们现在遍地的对比学习loss真的很像！很多道理都是相通的）

以上就是这篇文章的理论部分，其实很简单，但它提到的MoE的设计，启发了后续无数的工作。

接下来一篇则是时隔20多年后的另一篇经典论文，可能也是大家更熟悉的MoE工作。

Outrageously Large Neural Networks

  • 期刊/会议：ICLR'17
  • 论文链接：Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer
  • 代表性作者：Quoc Le, Geoffrey Hinton, Jeff Dean
    这篇文章，从title上就可以看出来它的背景和目的——希望做出极大的神经网络。在此之前，有很多 conditional computational 的工作，在理论上可以在有限的计算成本内把模型做的非常大，但是那些方法在具体实现的时候，有各种各样的问题。这篇文章提出了 Sparsely-Gated Mixture-of-Experts layer ，声称终于解决了传统 conditional computational 的问题，在牺牲极少的计算效率的情况下，把模型规模提升1000多倍。

Sparsely-Gated Mixture-of-Experts layer

跟1991年那个工作对比，这里的MoE主要有两个区别：

  • Sparsely-Gated：不是所有expert都会起作用，而是极少数的expert会被使用来进行推理。这种稀疏性，也使得我们可以使用海量的experts来把模型容量做的超级大。
  • token-level：前面那个文章，是 sample-level 的，即不同的样本，使用不同的experts，但是这篇则是 token-level 的，一个句子中不同的token使用不同的experts。
    这篇文章是在RNN的结构上加入了MoE layer：

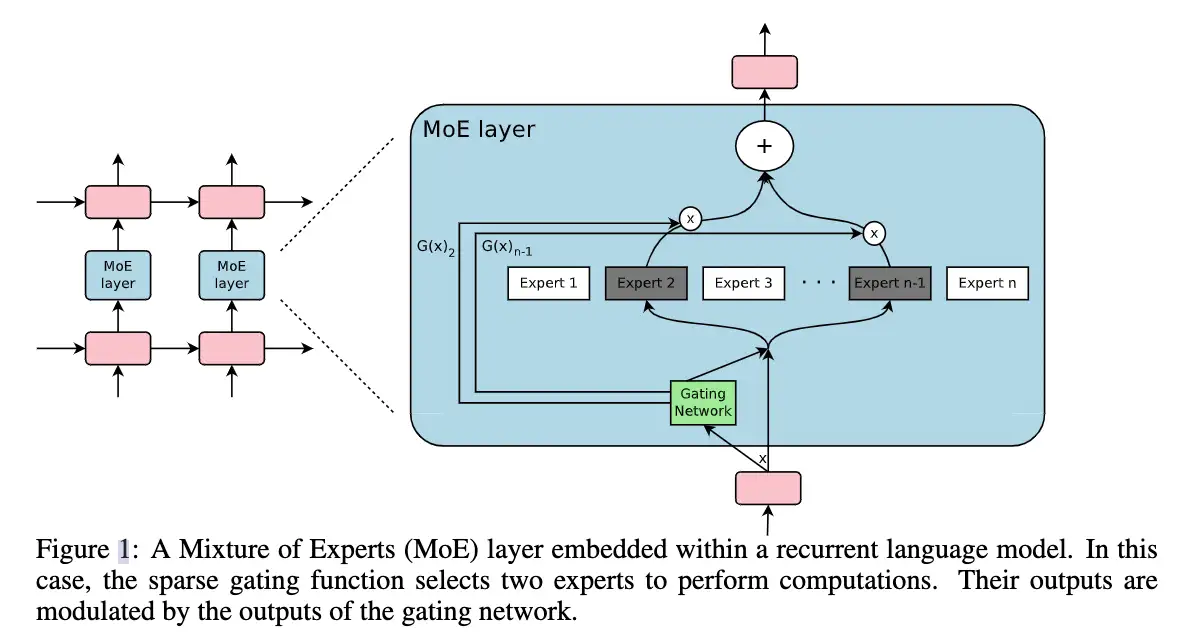
image

如图所示，每个token对应的position，都会有一个MoE Layer，每个MoE layer中包含了一堆的experts，每个expert都是一个小型的FFN，还有一个gating network会根据当前position的输入，选择少数几个expert来进行计算。

Gating Network

设 \(G(x)\) 和 \(E_i(x)\) 分别是 gating network 和第 \(i\) 个 expert 的输出，那么对于在当前position的输入\(x\)，输出就是所有 experts 的加权和(跟第一篇论文的第一个公式类似)：

\[ y=\sum_{i=1}^nG(x)_iE_i(x) \]

但是这里我们可能有上千个 experts，如果每个都算的话，计算量会非常大，所以这里的一个关键就是希望 \(G(x)\) 的输出是稀疏的，只有部分的 experts 的权重是大于 0 的，其余等于 0 的 expert 直接不参与计算。

首先看传统的 gating network 如何设计：

\[ G_\sigma(x)=Softmax(x\cdot W_g) \]

然后，作者加入了 sparsity 和 noise，具体来说：

  1. 添加一些噪声
  2. 选择保留前 \(K\) 个值
  3. 应用Softmax
    总而言之，sparsity 是通过 TopK sampling 的方式实现的，对于非 TopK 的部分，由于值是负无穷，这样在经过 softmax 之后就会变成 0，就相当于关门了。noise 项则可以使得不同 expert 的负载更加均衡。在具体实验中，作者使用的K=2~4.

我们为什么要添加噪声呢？这是为了专家间的负载均衡！

Expert Balancing

作者在实验中发现，不同 experts 在竞争的过程中，会出现“赢者通吃”的现象：前期变现好的 expert 会更容易被 gating network 选择，导致最终只有少数的几个 experts 真正起作用。因此作者额外增加了一个 loss，来缓解这种不平衡现象，公式如下：

\[ Importance(X) = \sum_{x\in X}G(x)\\ L(X) = \lambda\cdot CV(Importance(X))^2 \]

其中 \(X\) 代表的是一个batch的样本，把一个batch所有样本的gating weights加起来，然后计算变异系数（ coefficient of variation）。总之，这个反映了不同 experts 之间不平衡的程度。最后这个 loss 会加到总体 loss 中，鼓励不同的 experts 都发挥各自的作用。

上面就是 Sparsely-Gated MoE的主要理论，作者主要在 language modeling 和 machine translation 两个任务上做了实验，因为这两个任务，都是特别受益于大数据和大模型的，而本文的MoE的作用主要就在于极大地扩大了模型容量——通过MoE，把RNN-based网络做到了137B（1.3千亿）参数的规模，还是挺震撼的。效果自然也是极好的，我就不细说了。

GShard

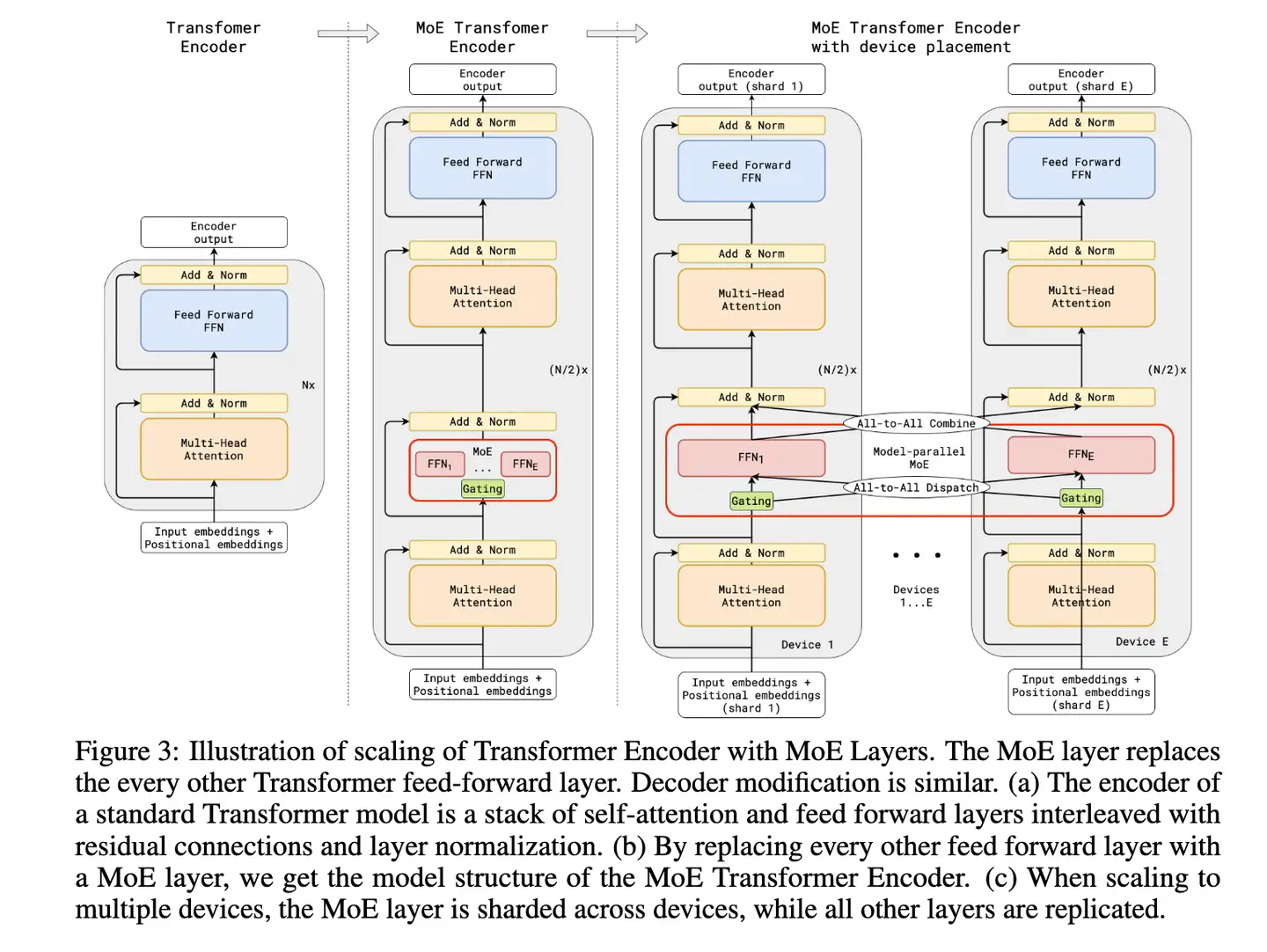
image

文中还提到了很多其他设计：

  • Expert capacity balancing：强制每个expert处理的tokens数量在一定范围内
  • Local group dispatching：通过把一个batch内所有的tokens分组，来实现并行化计算
  • Auxiliary loss：也是为了缓解“赢者通吃”问题, 下面伪代码中13行：
  • Random routing：在Top-2 gating的设计下，两个expert如何更高效地进行routing
    image

具体细节见论文。

Switch Transformers

Swith Transformer 的主要亮点在于——简化了MoE的routing算法，从而大大提高了计算效率。

结构如下：

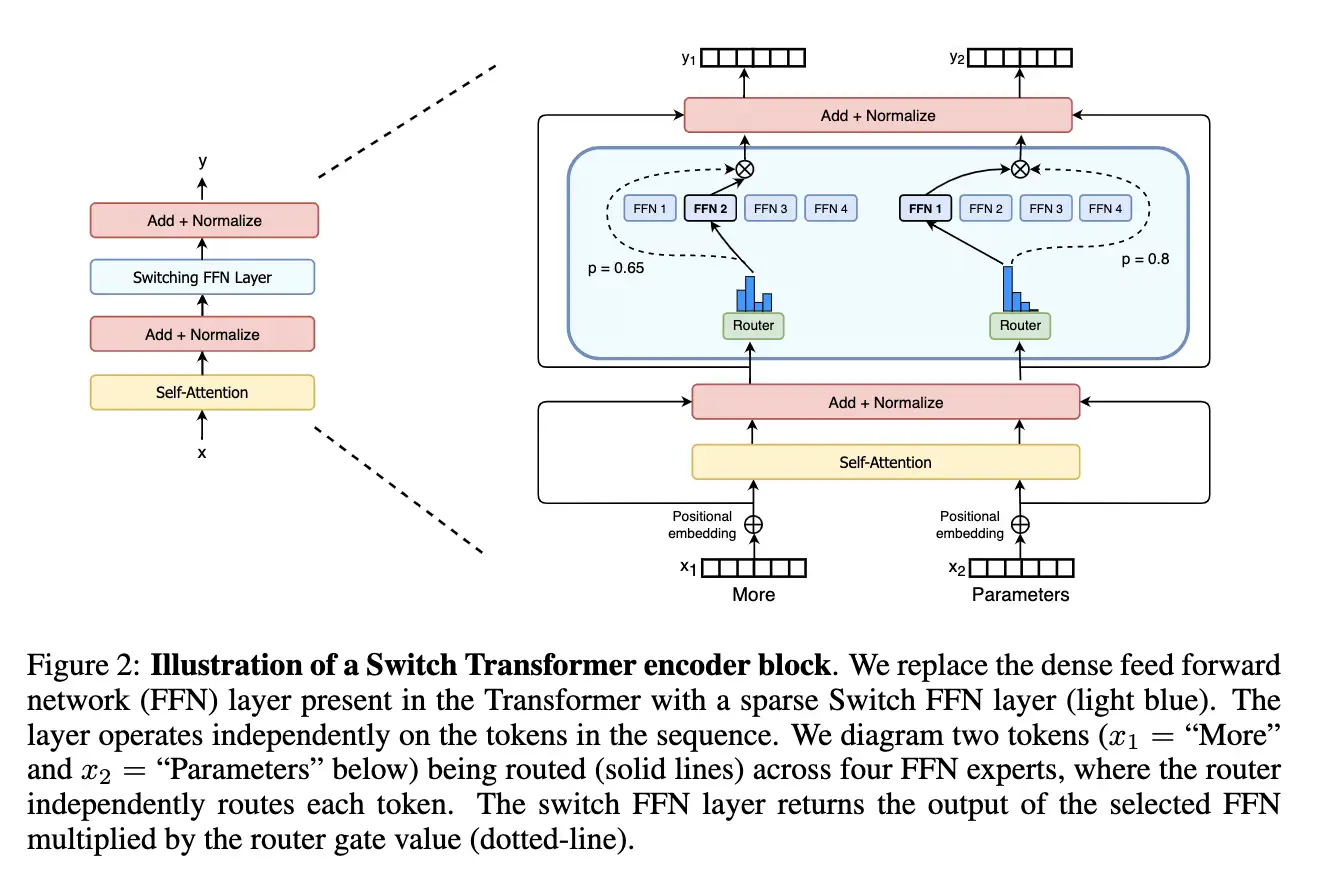
image

Swith Transformer 在论文中提到其设计的指导原则是——尽可能地把Transformer模型的参数量做大！（同时以一种简单高效的实现方式）

跟其他MoE模型的一个显著不同就是，Switch Transformer 的 gating network 每次只 route 到 1 个 expert，而其他的模型都是至少2个。这样就是最稀疏的MoE了，因此单单从MoE layer的计算效率上讲是最高的了。

下图展示了在同样的计算开销下，增大 experts 个数带来的性能提升，反正就是全面吊打T5，而且效率还一样：

image

GLaM