Deformable Convolution

在正式介绍这个工作之前很有必要先了解什么是 Deformable Convolution 。

Deformable Convolution 是MSRA的代季峰老师以及实习生在2017年提出的一种全新的卷积结构。这种方法将固定形状的卷积过程改造成了能适应物体形状的可变的卷积过程，从而使结构适应物体形变的能力更强。

传统的CNN只能靠一些简单的方法(比如max pooling)来适应物体的形变，如果形变的太厉害就无能为力了。因为CNN的卷积核的geometric structure是fixed的，也就是固定住的。卷积核总是在固定位置对输入特征特征进行采样。

为了改变这种情况专家们想了很多方法，最常见的有两种：

使用大量的数据进行训练。比如用ImageNet数据集，再在其基础上做翻转等变化来扩展数据集，通俗地说就是通过穷举的方法使模型能够适应各种形状的物体，这种方法收敛较慢而且要设计复杂的网络结构才能达到理想的结果。
设计一些特殊的算法来适应形变。比如SIFT，目标检测时用滑动窗口法来适应目标在不同位置上的分类也属于这类。
对第一种方法，如果用训练中没有遇到过的新形状物体(但同属于一类)来做测试，由于新形状没有训练过，会造成测试不准确，而且靠数据集来适应形变的训练过程太耗时，网络结构也必须设计的很复杂。

对于第二种方法，如果物体的形状极其复杂，要设计出能适应这种复杂结构的算法就更困难了。

为了解决这个问题，即CNN的卷积核的geometric structure是fixed的问题，代季峰老师等人提出 Deformable Convolution 方法，它对感受野上的每一个点加一个偏移量，偏移的大小是通过学习得来的，偏移后感受野不再是个正方形，而是和物体的实际形状相匹配。这么做的好处就是无论物体怎么形变，卷积的区域始终覆盖在物体形状的周围。

下图1是个示意图，a中绿色的点是原始的感受野范围，b~c中的蓝色点是对感受野加上偏移量后的新的感受野位置，可以看到叠加偏移量的过程可以模拟出目标移动、尺寸缩放、旋转等各种形变。c,d是b的特殊情况，显示了可变形卷积概括了比例、纵横比和旋转的各种变换。

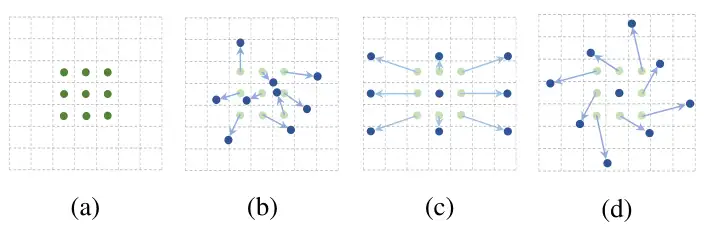
传统的卷积结构可以定义成式1，其中 $p_n$ 是卷积输出每一个点相对感受野上的每一个点的偏移量，取整数。

\[ \begin{equation} \mathbf{y}(\mathbf{p}_0)=\sum_{\mathbf{p}_n\in\mathcal{R}}\mathbf{w}(\mathbf{p}_n)\cdot \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n), \end{equation} \tag{1} \]

式中， $\mathcal{R}=\{(-1, -1), (-1, 0), \ldots, (0,1), (1, 1)\}$是卷积核。

采用全新的可变形卷积后要在公式1基础上给每个点再增加一个偏移量 $\Delta \mathbf{p}_n$ ，这个新的偏移量是由另一个卷积得出，所以一般是小数，见式2。

\[ \begin{equation} \mathbf{y}(\mathbf{p}_0)=\sum_{\mathbf{p}_n\in\mathcal{R}}\mathbf{w}(\mathbf{p}_n)\cdot \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n). \end{equation} \tag{2} \]

式2中的 $\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n$ 的取值位置非整数，并不对应feature map上实际存在的点，所以必须用插值来得到，如果采用双线性插值的方法，可以变成式3。其中 $\mathbf{x}(\mathbf{q})$ 表示feature map上所有整数位置上的点的取值， $ \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n)$ 表示加上偏移后所有小数位置的点的取值。

\[ \begin{align} \mathbf{x}(\mathbf{p})&=\sum_\mathbf{q} G(\mathbf{q},\mathbf{p})\cdot \mathbf{x}(\mathbf{q})\\ &=\sum_\mathbf{q} g(q_x,p_x)\cdot g(q_y,p_y)\cdot \mathbf{x}(\mathbf{q})\\ &=\max{(0,1-|q_x-p_x|)}\cdot \max{(0,1-|q_y-p_y|)} \cdot \mathbf{x}(\mathbf{q}) \end{align} \tag{3} \]

式3是怎么推导出的呢？先拿最简单的例子来做说明，如下图2所示，假设feature map只有4个点，则其中插入一个点 $P(x,y)$ 的值可以用式 3来得到，这就是双线形插值的标准公式，对于相邻的点来说 $x_1-x_0=1,y_1-y_0=1$。

\[ \begin{align} \text{Pixel}(x,y) &=(x_1-x)(y_1-y)\text{Pixel}(x_0,y_0)\\ &+(x-x_0)(y_1-y)\text{Pixel}(x_1,y_0)\\ &+(x_1-x)(y-y_0)\text{Pixel}(x_0,y_1)\\ &+(x-x_0)(y-y_0)\text{Pixel}(x_1,y_1)\\ \end{align} \tag{4} \]

完整的可变形卷积的结构可以参考下图3，注意上面的卷积用于输出偏移量，该输出的长宽和输入特征图的长宽一致，维度则是输入的2倍(因为同时输出了x方向和y方向的偏移量，要用2个维度分开存储)。

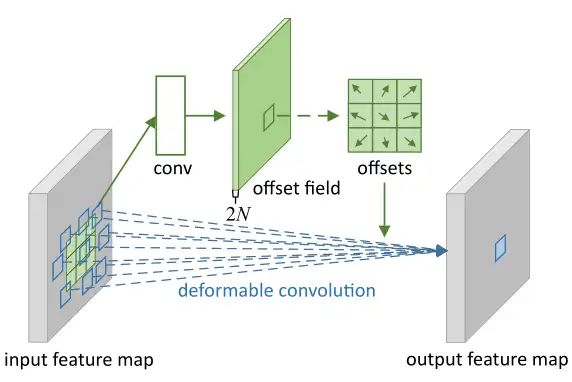
Deformable Convolution 对偏差的反向传播的计算方法：

\[ \begin{equation} \begin{split} \frac{\partial \mathbf{y}(\mathbf{p}_0)}{\partial \Delta \mathbf{p}_n} & = \sum_{\mathbf{p}_n\in\mathcal{R}}\mathbf{w}(\mathbf{p}_n)\cdot \frac{\partial \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n)}{\partial \Delta \mathbf{p}_n} \\ = \sum_{\mathbf{p}_n\in\mathcal{R}} & \left[\mathbf{w}(\mathbf{p}_n)\cdot \sum_\mathbf{q} \frac{\partial G(\mathbf{q}, \mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n)}{\partial \Delta \mathbf{p}_n} \mathbf{x}(\mathbf{q})\right], \\ \end{split} \end{equation} \tag{5} \]

实验效果

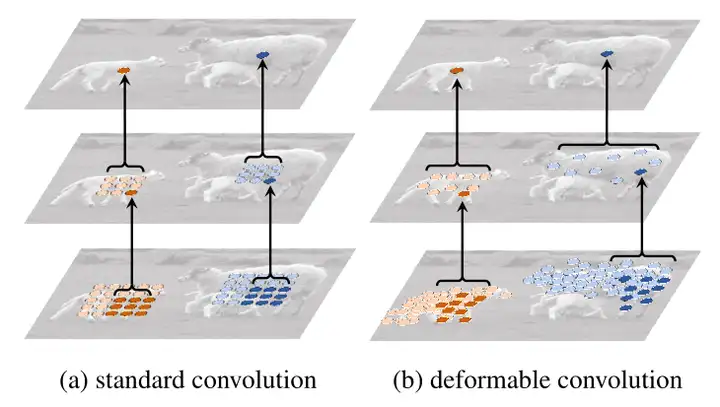
如图4所示为标准卷积中和Deformable卷积中的receptive field，采样位置(sampling locations)在整个顶部特征图(左)中是固定的。它们根据可变形卷积中对象的比例和形状进行自适应调整(右)。可以看到经过两层的传统卷积和两层的Deformable卷积的对比结果。左侧的传统卷积单个目标共覆盖了55=25个采样点，感受野始终是固定不变的方形；右侧的可变形卷积因为感受野的每一个点都有偏移量，造成卷积核在图片上滑动时对应的感受野的点不会重复选择，这意味着会采样99=81个采样点，比传统卷积更多。

如图5所示展示了4组图片，每组是3张，分别代表使用3层的 Deformable Convolution 时，同一个image中背景(background)，小物体(small object)，大物体(big object)的sampling locations，绿色小点为第一层采样的中心点，就像图6中第1层的中心点一样。

图5是连续三级可变形卷积带来的效果，每一级卷积都用3*3的卷积核做卷积，三层卷积后就能产生93=729个采样点。可以看到经过训练后所有的采样点都偏移到了目标周围。

我们发现，Deformable Convolution使得采样点不是均匀分布，打破了固定的采样位置，采样点刚好分布在物体的内部，根据可变形卷积中对象的比例和形状进行自适应调整，这有利于检测任务性能的提升。

作者认为可形变卷积的优势还是很大的，包括：

对物体的形变和尺度建模的能力比较强。
感受野比一般卷积大很多，因为有偏移的原因，实际上相关实验已经表明了DNN网络很多时候受感受野不足的条件制约；但是一般的空洞卷积空洞是固定的，对不同的数据集不同情况可能最适合的空洞大小是不同的，但是可形变卷积的偏移是可以根据具体数据的情况进行学习的。

Deformable DETR

DETR回顾

DETR利用了Transformer通用以及强大的对相关性的建模能力，来取代anchor，proposal等一些手工设计的元素。但是DETR依旧存在2个缺陷：

训练时间极长：相比于已有的检测器，DETR需要更久的训练才能达到收敛(500 epochs)，比Faster R-CNN慢了10-20倍。
计算复杂度高：发现DETR对小目标的性能很差，现代许多种检测器通常利用多尺度特征，从高分辨率(High Resolution)的特征图中检测小物体。但是高分辨率的特征图会大大提高DETR复杂度。
产生上面2个问题的原因是：

在初始化阶段，对于特征图中的所有pixel的权重是Uniform的，导致要学习的注意力权重集中在稀疏的有意义的位置这一过程需要很长时间，意思是从Uniform到Sparse and meaningful需要很久。
attention map是 $N_q\times N_k$ 的，在图像领域我们一般认为 $N_q= N_k=N_v=N=HW$ 所以里面的weights的计算是像素点数目的平方。因此，处理高分辨率特征图需要非常高的计算量，存储也很复杂。

所以，Deformable DETR的提出就是为了解决上面的2个问题，如上图所示，即：收敛速度慢和计算复杂度高的问题。它主要利用了可变形卷积(Deformable Convolution)的稀疏空间采样的本领，以及Transformer的对于相关性建模的能力。针对此提出了一种 $\color{purple}{\text{Deformable Attention Module}}$，这个东西只关注一个feature map中的一小部分关键的位置，起着一种pre-filter的作用。这个 deformable attention module 可以自然地结合上FPN，我们就可以聚集多尺度特征。所以，作者就使用它来替换Transformer的 attention module 。

在Transformer的 Multi-Head Attention 中，一个Query element会和一组Key element做scaled dot-product attention，多头注意力模块根据这个attention的权重自适应地聚集关键内容。为了使模型能够学习到不同位置的内容，不同attention Head的输出线通过Linear Projection得到最后的结果。用公式可以表达为：

\[ \begin{equation} \text{MultiHeadAttn}(z_q, x_k) = \sum_{m=1}^{M} \mathrm{W}_m \big[\sum_{k\in\Omega_k} A_{mqk} \cdot \mathrm{W'}_m x_k \big], \end{equation} \tag{6} \]

其中，变量的定义如下：

$m$ 是指 Multi-Head Attention 的第 $m$ 个head。
$x\in HW\times C$ 为这个 Multi-Head Attention 的 Key 和 Value 输入特征，可以分解成 $N=HW$ 个 $x_k$ ，其中$x_k \in R^{C}$ ，为输入特征的一部分。 $x$ 通常是输入embedding与Positional的加和。
$\mathrm{W'}_m\in C_v\times C\;(C_v=C/M)$为从输入特征到 Value 的Transformation Matrix， $\mathrm{W}_m\in C_v\times C$ 为从输入特征到 Key 的Transformation Matrix。
$A_{mqk} \propto \exp\{\frac{z_q^T \mathrm{U}_m^T~ \mathrm{V}_m x_k}{\sqrt{C_v}}\}$ 是标量，表示第 $m$ 个head的第 $q$ 个 Query 与第 $k$ 个 Key 之间的attention是多少。
$z\in HW\times C$ 为这个 Multi-Head Attention 的 Query 输入特征，可以分解成 $N=HW$ 个 $z_q$ ，其中 $z_q \in R^{C}$ ，为输入特征的一部分。 $z$ 通常是输入embedding与Positional的加和。
$\mathrm{U}_m\in C_v\times C\;(C_v=C/M)$ 为从输入特征到 Query 的Transformation Matrix。
$\sum_{k\in\Omega_k}$ 其实就是attention weights与 Value 的weighted sum过程。
以上(6)式就是表达了 Multi-Head Attention 的功能。

我们注意到： $ \mathrm{U}_m z_q$ 就是 Query ，而 $ \mathrm{V}_m x_k$ 就是 Key ，而在初始化以后，它们一般服从 $\mu=0,\sigma=1$ 的正态分布。这就使得当 $N_k$ 很大时有 $A_{mqk}\simeq\frac{1}{N_k}$ ，这将导致attention weights的差别不大。在视觉领域，一般 $N_k=HW$ ，这个值刚好较大。因此，需要长时间的训练，以便注意力可以集中在特定的 Key 上。

我们再来评估下上式(6)的计算复杂度：

\[ O(N_qC^2 + N_kC^2 + N_qN_kC) \tag{7} \]

这一项具体是如何得到的？这里提供一种理解方法：

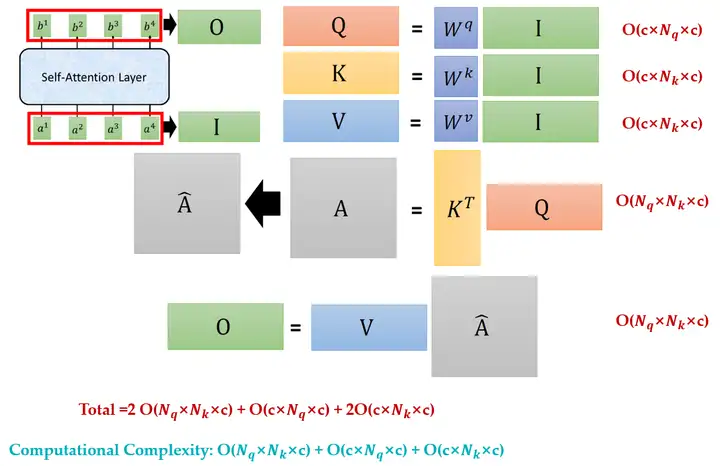
如上图7所示，Self-attention可以用一堆矩阵的乘法表示，所以可以使用GPU加速。其中的每一步的计算复杂度已经在图中标注出来：

计算 Value 的计算复杂度： $O(N_kC^2)$

计算 Key 的计算复杂度：$O(N_kC^2)$

计算 Query 的计算复杂度：$O(N_qC^2)$

计算 Attention Matrix 的计算复杂度： $O(N_qN_kC)$

计算多个 head 变成一个 head 的Linear Transformation 的计算复杂度： $O(N_q m C^{\prime}C)=O(N_qC^2)$

计算 Output 的计算复杂度： $O(N_qN_kC)$

所以一共是： $2O(N_qN_kC)+2O(N_qC^2)+2O(N_kC^2)$

所以总的计算复杂度是： $O(N_qC^2 + N_kC^2 + N_qN_kC)$

一般有 $N_q=N_k=N>>C$，因此，计算复杂度可以近似为 $O(N_qN_kC)$。所以多头注意力模块随着特征图尺寸而遭受二次复杂度增长。

我们回顾下DETR模型的计算复杂度，它的Transformer的结构如下图8所示：

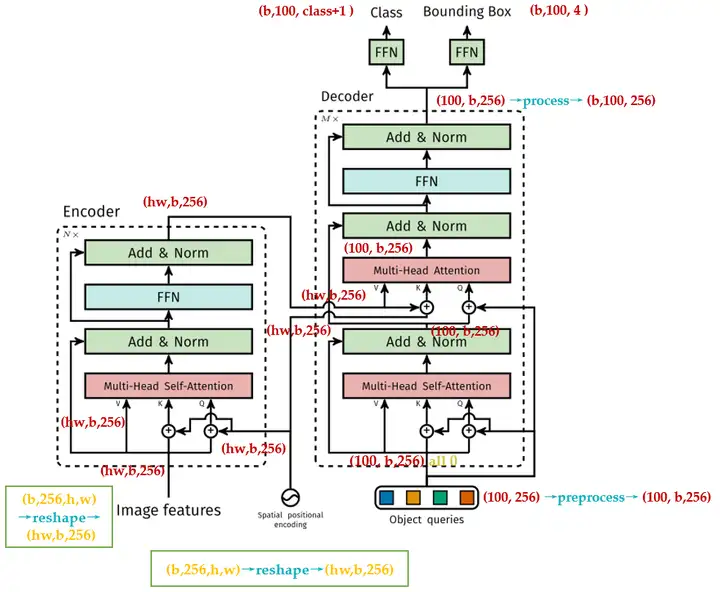
编码器的每个Block中只有一个 Multi-Head Attention ， Query,Key,Value 都来自图像特征，所以 $N_q=N_k=HW$ ，所以编码器的计算复杂度是 $O(H^2W^2C)$。
编码器的每个Block中有2个 Multi-Head Attention ，
第1个的Query,Key,Value 都来自object queries，所以 $N_q=N_k=N$ ，所以编码器的计算复杂度是 $O(2NC^2+N^2C)$ 。
第2个的Query 来自object queries， Key,Value 来自编码器输出，所以 $N_q=N,N_k=HW$ ，所以编码器的计算复杂度是 $O(HWC^2+NC^2+HWNC)=O(HWC^2+HWNC)$ 。
DETR在探测小物体方面的性能相对较低。与现代目标检测器相比，DETR需要更多的训练epoches才能收敛。这主要是因为处理图像特征的注意模块很难训练。所以本文提出了 Deformable Attention Module 。设计的初衷是：传统的 attention module 的每个 Query 都会和所有的 Key 做attention，而 Deformable Attention Module 只使用固定的一小部分 Key 与 Query 去做attention，所以收敛时间会缩短。

Deformable Attention Module 的原理

首先对比下二者在表达式上的差别：下式(8)为常规的 attention module ，(9)为 Deformable Attention Module 。

首先对比下紫色的部分，在常规 attention module 中， $k\in\Omega_k$ ，即要考虑所有的 Key ；而在 Deformable Attention Module 中 $k\in [1,K](K\ll HW)$ ，即只要考虑一小部分的 Key ，每个 Query 只采样 $K$ 次，即：只需要考虑 $K$ 个 Key 。

\[ \begin{equation} \text{MultiHeadAttn}(z_q, x_k) = \sum_{m=1}^{M} \mathrm{W}_m \big[{\color{purple}\sum_{k\in\Omega_k}} A_{mqk} \cdot \mathrm{W'}_m {\color{crimson}{x_k} }\big], \end{equation} \tag{8} \]

\[ \begin{equation} \text{DeformAttn}(z_q, p_q, x) = \sum_{m=1}^{M} \mathrm{W}_m \big[{\color{purple}{\sum_{k=1}^{K}}} A_{mqk} \cdot \mathrm{W'}_m x{\color{crimson}{(p_q + \Delta p_{mqk})}}\big], \end{equation} \tag{9} \]

再对比下红色的部分，在常规 attention module 中，分别取 $N_k$个 $x_k$ ，然后把结果作weighted sum；而在 Deformable Attention Module 中， $x\in C\times H\times W$ ，设 $p_q$ 是2-D空间上的任意一点，首先与一个2-D实数值 $ \Delta p_{mqk}$ 相加，再通过bilinear interpolation得到新的feature map的一点。

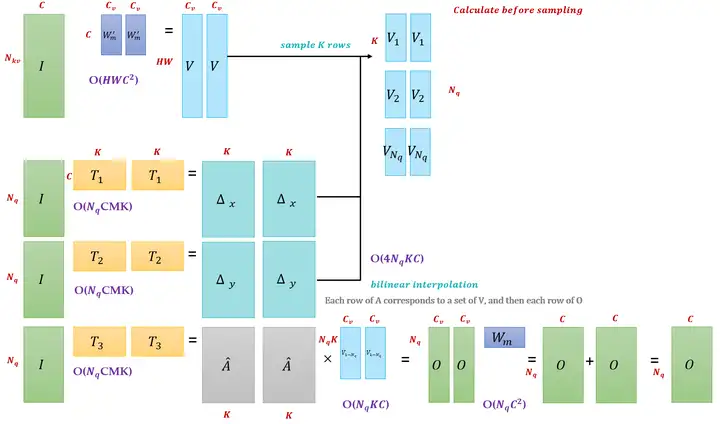
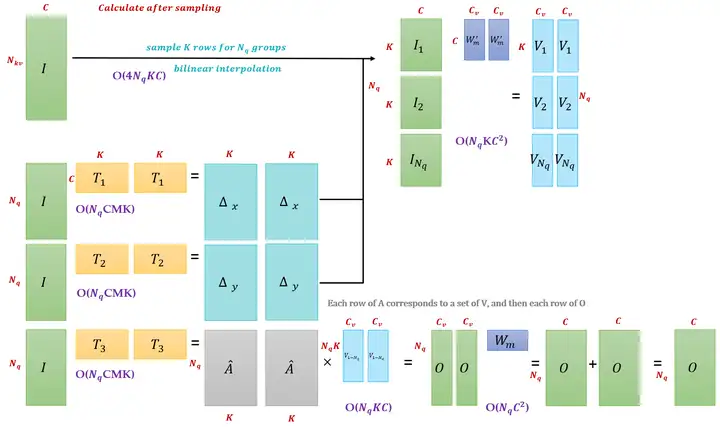
图9的这2张图为 Deformable Attention Module 的2种形式，我们可以与之前的 self-attention module 做个比较看看二者有何不同，我们发现：

Deformable Attention Module 的 Attention 矩阵不是由 Query 和 Key 作内积得到的，而是由输入特征 $I$ 直接通过 Linear Transformation 得到的。

以上面的图为例：

我们假设输入特征 $I$ 的维度是 $(N_q,C)$ ，它与几个转移矩阵相乘，得到一个大的张量，我们在图中把这个东西分开画成了 $\Delta_x, \Delta_y,\hat A$，它们的维度都是 $(N_q,MK)$ 。其中， $\hat A$ 代表Attention，一会要与 Value 做weighted sum得到输出。
$\Delta_x, \Delta_y$ 代表相对参考点的偏移量， Query 可以看做是 $N_q$ 个向量，对于Encoder来讲， $N_q=HW$ ，即特征图的每个点都是一个向量， $\Delta_x, \Delta_y$ 表示的就是特征图上的某一点 $(x,y)$ 对应的 Value 的位置，因为 Value 的维度是 $(HW,C)$ 维的，所以有 $HW$ 个位置可以对应，我们需要的就是其中的 $K$ 个位置，那具体是哪 $K$ 个位置，就是由 $\Delta_x, \Delta_y$ 计算得到的。
同时，输入特征 $I$ 再与转移矩阵 $W_m^{\prime}$ 相乘得到 ${\text{Value}}\in (HW,C)$ 。结合刚才计算的 $\Delta_x, \Delta_y,\hat A$ ，我们需要为 $N_q$ 维的 Query 中的每一个采样 $K$ 个分量。
所以采样之后的 ${\text{Value}}\in (N_q,K,C)$ ， $M$ 个head的 Value 就是 ${\text{Value}}\in (N_q,M, K,C)$ 。我们把它分成 $N_q$ 组，每组的 ${\text{Value}}\in (M,K,C)$ 。
接下来我们使用 $\hat A$ 中的每一行分别与每一组 ${\text{Value}}\in (M,K,C)$ 做weighted sum，并把结果拼在一起，得到 $O\in (N_q,M,C_v)$ 的输出，最后作Linear Transformation把这些head的输出合并为一个输出 $O\in (N_q,C),C=MC_v$ 。
再以下面的图为例：
先对计算 Value 的输入特征 $I\in (N_{kv},C)$ 采样成 $N_q$ 组，每组的采样后的输入特征为 $I\in (K,C)$ 。然后，对这 $N_q$ 组的输入特征乘以transformation matrix得到 $N_q$ 组，每组的 ${\text{Value}}\in (M,K,C_v)$ 。所以 Value 还是$\in (N_q,M,K,C_v)$ 。
计算 $\Delta_x, \Delta_y,\hat A$ 的过程与上方的图一致，最后得到的输出 $O\in (N_q,C),C=MC_v$ 。