补充知识
- 表示学习（Representation Learning）：学习数据的表征，以便在构建分类器或其他预测器时更容易提取有用的信息，无监督学习也属于表示学习。
- 互信息（Mutual Information）：表示两个变量 \(X\) 和 \(Y\) 之间的关系，定义为：
- 对比损失(contrastive loss)：计算成对样本的匹配程度，主要用于降维中。计算公式为：
- 噪声对抗估计（Noise Contrastive Estimation, NCE）：在NLP任务中一种降低计算复杂度的方法，将语言模型估计问题简化为一个二分类问题。
- 负采样（Negative Sampling, NEG）：表示负采样，是NCE的一个简化版本，目的是提高训练速度，改善所得词向量的质量。采用了相对简单的随机负采样，本文中选择数据集中一个是正样本，其他均为负样本。
问题提出
目前，表示学习的主要问题在于，网络学习到的特征往往都只适用于特定的任务，其泛化性能有待提升。最近的无监督学习都沿用了最普遍的方法：预测未来的、缺失的或上下文的特征，因此无监督学习可以定义为预测问题，将预测到的特征再用于表示学习。
论文主要工作：
1、将高维数据编码到一个更容易对任务进行建模的低维隐空间中；
2、在隐空间中运用了一个强大的自回归模型，来预测未来特征或步骤；
3、为了实现端到端的网络训练，使用了对抗噪声估计作为损失函数。
本文的直观思路是学习能编码高维信息的不同部分的underlying shared information的表征，同时抛弃掉更local的low-level信息和噪声。简单来说，按那位大佬的说法，预测未来输出是不可能的，你怎么知道下一步的输出是什么。那么，要做的是就是预测的输出与实际的下一步输出尽可能相似，要做到这一点，就需要Prediction中尽可能包含invariance和global的structure。作者将这些部分定义为“slow features”，并用speech任务中的phonemes和intonation，图像任务中的objects或books中的story line来举例。
预测高维数据的难点之一是均方误差和交叉熵这样的单峰损失效果不好，而如果使用一个强大的条件生成模型对每个细节进行重建，就会需要很大的计算量，并且会忽略了数据集 \(x\) 中的上下文关系 \(c\)。同时，使用label，这种高级潜在变量，也会丢失大量信息。（如一张图片最后被编码成10bit向量代表1024个类中的一个）从而 \(p(x|c)\) 并不能最优地抽取\(x\) 和 \(c\) 的共享信息。
最后作者提出了最大化 target x (future)和 context c (present) 的表征的交互信息的方法来抽取输入共享的潜在特征：
这里进一步解释一些互信息（mutual infomation），互信息实际上就是表示两个变量之间的相关性，上式也就是互信息的定义式的变形， \(I(x;c)\) 表示 \(x\) 与 \(c\) 的关系，但具体是什么关系呢？可以看如下的推导：
最终的结果是\(H(x)-H(x|c)\)，其中 \(H(x)\) 为\(x\)的熵，用来衡量\(x\)的不确定度，定义如下：
而 \(I(x;c)=H(x)-H(x|c)\) 也就说明了 \(x\) 与 \(c\)的互信息 即表示由于 \(c\) 的引入而使 \(x\) 熵减小的量，也就是 \(x\) 不确定度减小的量。因此，放在论文中的含义来看，最大化 \(I(x;c)\) 也就是通过充分学习现在的上下文 \(c\) 最大程度的减小了未来 \(x\) 的不确定度，从而起到了预测的效果，所以CPC希望网络可以最大化 \(x\) 和 \(c\) 之间的互信息。
Method
Contrastive Predicting Coding
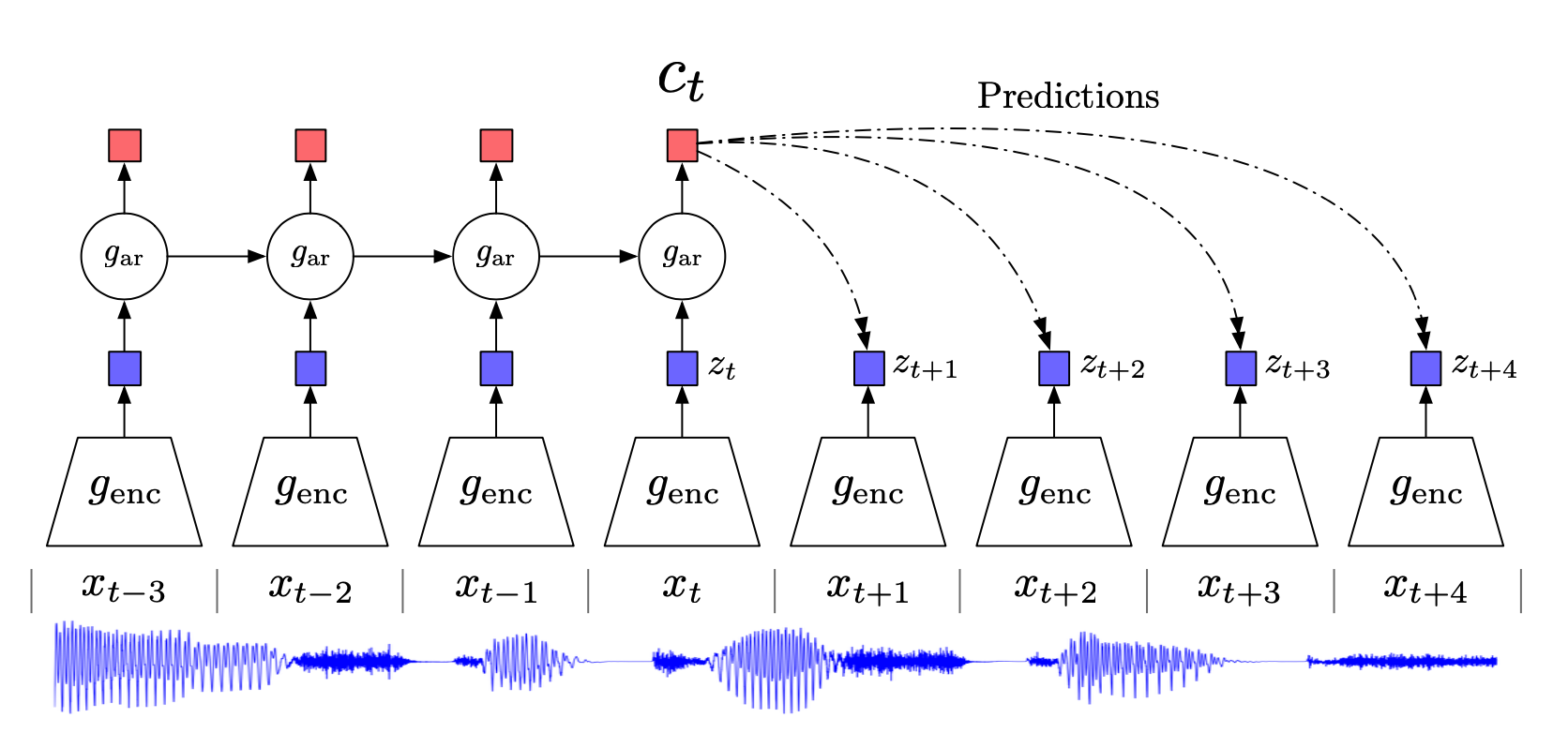
在这个图里，raw data是最下面的语音信号 \(\{x_t\}\)，我们想要找到一个好的representation vector \(\{z_t\}\)，这个\(\{z_t\}\) 不仅能尽可能地保留原信号 \(\{x_t\}\) 的重要信息，也有很好的预测能力。首先我们在原信号上选取一些时间窗口frames，对每一个frame，我们用一个有编码能力的函数（比如autoencoder或者cnn）\(g_{enc}\)。然后得到representation vector
接下来为了做预测，我们把\(\{z_t\}\) 放到一个可以做预测的model里，论文里不失一般性地用\(g_{ar}\) 来表示这个可以做预测的有自回归model，通常大家会用RNN(LSTM)，我们用t时刻及其之前的若干时刻输入这个回归模型，得到t时刻的涵盖了对过去信息的memory的输出 \(c_t=g_{ar}(z_{\leq t})\)。
接下来，我们希望 \(c_t\)是足够好的，是具有预测性质的。怎么评价它好不好呢？我们可以用 \(c_t\) 去预测之后k个时刻的latent vector（k是我们感兴趣的预测的步长）这里记作 \(\hat{z}_{t+1},\hat{z}_{t+2},...,\hat{z}_{t+k}\) 然后我们希望 \(\hat{z}_{t+i}\)（预测的latent vector）和 \(z_{t+i}\) (真实的 \(x_{t+i}\) 的latent vector）尽可能相似。
如果要用当前的 \(c_t\) 去预测 \(k\) 个时刻后的 \(z_{t+k}\) ，之前提到作者不采用生成模型 \(p(x_{t+k}|c_t)\) 进行预测，而是最大化 \(c_t\) 和 \(x_{t+k}\) 之间的互信息使得预测的 \(\hat{z}_{t+i}\) 与真实的 \(z_{t+i}\) 尽可能的相似。根据等式 (1)，我们没办法控制互信息中的 \(x\) 和 c 的联合分布概率 \(p(x,c)\) ，因此作者提出了一个密度比的概念，如下：
这里原作直接用线性矩阵 \(W_1,W_2,...,W_k\) 乘以 \(c_t\) 做的预测（也可以用rnn去做），然后用向量内积来衡量相似度。
于是也就有了原作里令人百思不得其解的函数：
这里\(f_k()\)其实是在计算 \(c_t\) 的预测和 \(x_{t+k}\)（真实的未来值）符不符合。
InfoNCE Loss
现在可以引入contrastive的概念了。
CPC用到了 Noise-Contrastive Estimation(NCE) Loss, 具体在这篇文献里定义为InfoNCE:
选取\(X=\{x_1,x_2,...,x_N\}\),这里面有一个是positive sample 来自于\(p(x_{t+k}|c_t)\), 其他N-1个是negative sample（noise sample）来自于 \(p(x_{t+k})\). Loss function定义如下：
怎么理解这个loss function呢。\(p(x_{t+k}|c_t)\) 指的是，我们选正在用的那个声音信号的\(x_{t+k}\)，而 \(p(x_{t+k})\) 指的是我们可以随便从其他的声音信号里选择一个片段。回忆一下，我们刚才说过，\(f_k()\)其实是在计算 \(c_t\) 的预测和 \(x_{t+k}\)（未来值）符不符合。那么对于随便从其他声音信号里选出的 \(x_j\)\(f_k(x_j,c_t)\) 应是相对较小的。
因此为了优化该损失，我们希望分子尽可能大，分母尽可能小。这也就符合我们对于 \(x\) 和 \(c\) 互信息的要求，即正样本对之间的互信息更大，负样本对之间的互信息更小。优化该损失，实际上就是最大化 \(x_{t+k}\) 和 \(c_t\) 间的互信息。上式实际上是一个正确分类正样本的多分类交叉熵损失。现在考虑该损失的最佳情况，假设 \(x_i\)是 \(c_t\) 预测的结果，即正样本，那么 \(x_i\) 被采样的概率如下，这实际上也就是等式2中定义的的最优输出结果：
可以看到 \(f_k(_{t+k},c_t)\) 确实与 \(\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}\) 成比例，并且与负样本选择的数量 \(N-1\) 无关，与前面所定义的密度比的概念相符合。
Mutual Information Estimation
虽然我们已经能够训练这个网络，但实际上我们可以具体推导 InfoNCE 和互信息之间的关系，以证明优化 InfoNCE loss 确实对在最大化互信息有帮助。由前面可以知道， \(f_k(_{t+k},c_t)\) 是由 \(\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}\) 决定，因此将其带入等式4中，并且将 \(X\) 分为正样本 \(x_{t+k}\) 和负样本 \(X_{neg}\) ：
所以最终得到：
优化 InfoNCE（最小化 \(L_N^{opt}\) ）也就是最大化 \(x_{t+k}\) 和 \(c_t\) 之间的互信息的下限，并且 \(N\) 越大，上面第三步中的约等于就越准确。另一方面，我们增加 \(N\) 的数量同样可以增大 \(I(x_{t+k},c_t)\) 的下限，因此有些其他方法会增大负样本的数量来提高效果。
Experiments for Vision
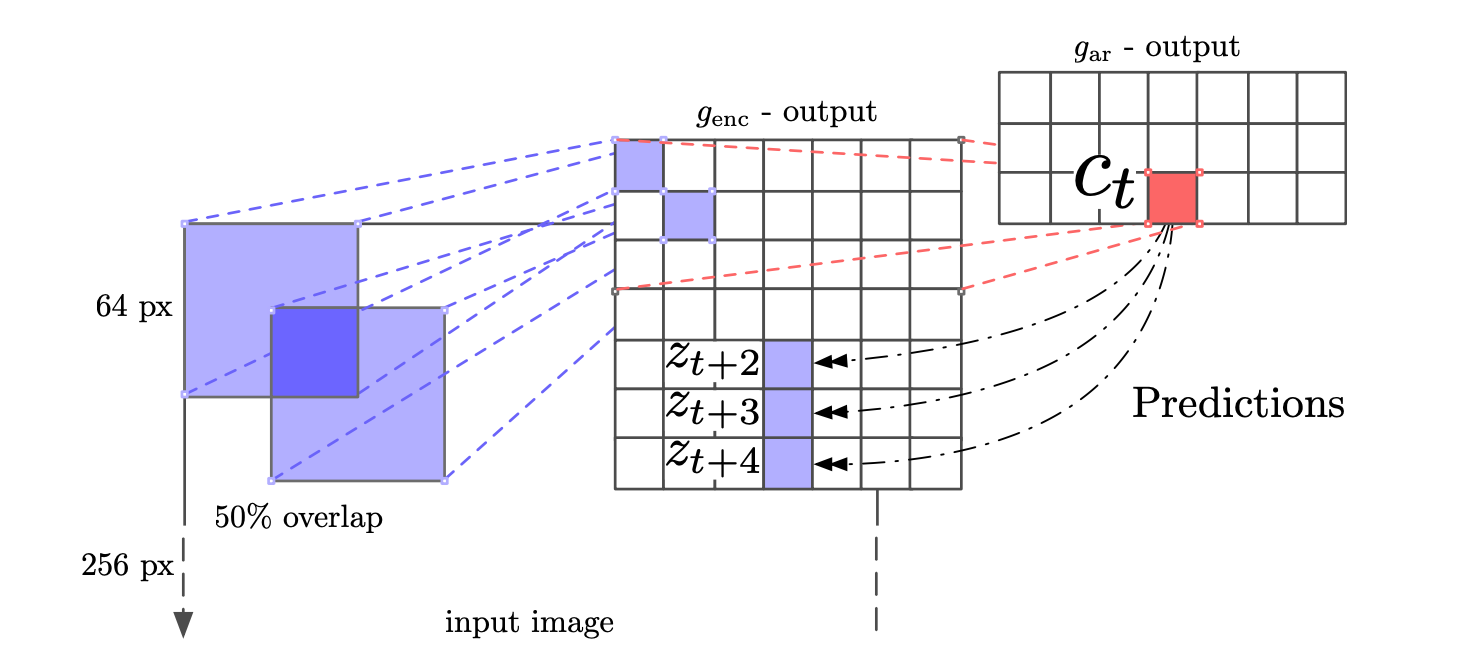
前面的 CPC 架构图是以语音模型为例，对于语音和文本，可以利用不同的\(k\)时间步长，来采集正样本，而负样本可以从序列随机取样来得到。
对于图像任务，可以使用类似 pixelCNN 的自回归模型将其转化成一个序列类型，用前几个 patch 作为输入，预测之后的 patch:
