概述

SSM的概念由来已久，但这里我们特指深度学习中的SSM，一般认为其开篇之作是2021年的 S4，不算太老，而SSM最新最火的变体大概是Mamba。当然，当我们谈到SSM时，也可能泛指一切线性RNN模型，这样RWKV、RetNet还有此前LRU都可以归入此类。不少SSM变体致力于成为Transformer的竞争者，尽管笔者并不认为有完全替代的可能性，但SSM本身优雅的数学性质也值得学习一番。

尽管我们说SSM起源于S4，但在S4之前，SSM有一篇非常强大的奠基之作《HiPPO: Recurrent Memory with Optimal Polynomial Projections》（简称HiPPO），所以本文从HiPPO开始说起。

另外值得一提的是，SSM代表作HiPPO、S4、Mamba的一作都是Albert Gu，他还有很多篇SSM相关的作品，毫不夸张地说，这些工作筑起了SSM大厦的基础。不论SSM前景如何，这种坚持不懈地钻研同一个课题的精神都值得我们由衷地敬佩。

今天，基本上你能叫出的任何语言模型都是 Transformer 模型。OpenAI 的 ChatGPT、谷歌的 Gemini 和 GitHub 的 Copilot 等都是由 Transformer 驱动的，仅举几个例子。然而，Transformer 存在一个基本缺陷：它们由 Attention 驱动，其扩展速度与序列长度呈二次方关系。简单来说，对于快速交流（让 ChatGPT 讲一个笑话），这没问题。但对于需要大量文字的查询（让 ChatGPT 总结一份 100 页的文档），Transformer 可能会变得过于缓慢。

SSM系列就是这种线性时间语言模型

状态空间模型(State Space Model, SSM)

什么是状态空间？

状态空间包含完全描述系统所需的最小变量数。它是通过定义系统的可能状态来数学地表示问题的方法。

让我们稍微简化一下。想象我们正在迷宫中导航。 “状态空间”是所有可能位置（状态）的地图。每个点代表迷宫中一个独特的位置，具有特定的细节，比如你离出口有多远。

“状态空间表示”是对此图的简化描述。它显示了当前的位置（当前状态）、可以前往的地方（可能的未来状态），以及哪些变化能进入下一个状态（向右或向左）。

描述状态的变量，在我们的例子中是 \(X\) 和 \(Y\) 坐标，以及到出口的距离，可以表示为“状态向量”。

听起来熟悉吗？这是因为语言模型中的嵌入或向量也常被用来描述输入序列的“状态”。例如，你当前位置（状态向量）的向量可能看起来有点像这样：

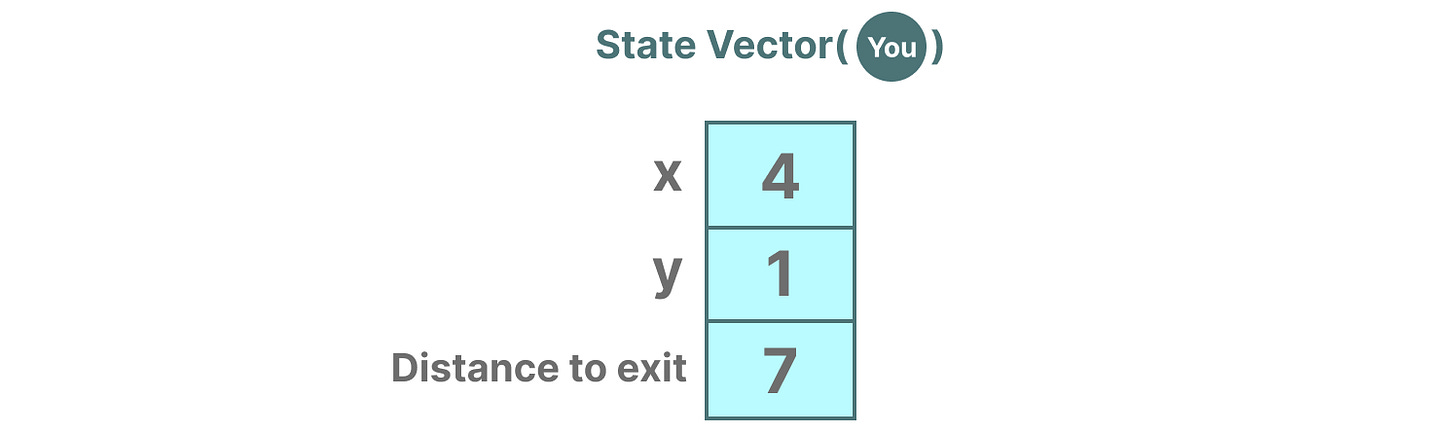
在神经网络中，系统的“状态”通常是其隐藏状态，在大型语言模型的背景下，生成新标记最重要的方面之一。

什么是状态空间模型？

SSMs 是用于描述这些状态表示并基于某些输入预测其下一个状态可能是什么的模型。

传统上，在时间 \(t\)，状态空间模型（SSMs）:

将输入序列 \(x(t)\) 进行映射（例如，在迷宫中向左下方移动）
转换为潜在状态表示 \(h(t)\)（例如，距离出口和 \(x/y\) 坐标）
并推导出预测输出序列 \(y(t)\)（例如，再次向左移动以更快到达出口）
然而，它不是使用离散序列（如向左移动一次）作为输入，而是接受一个连续序列并预测输出序列。

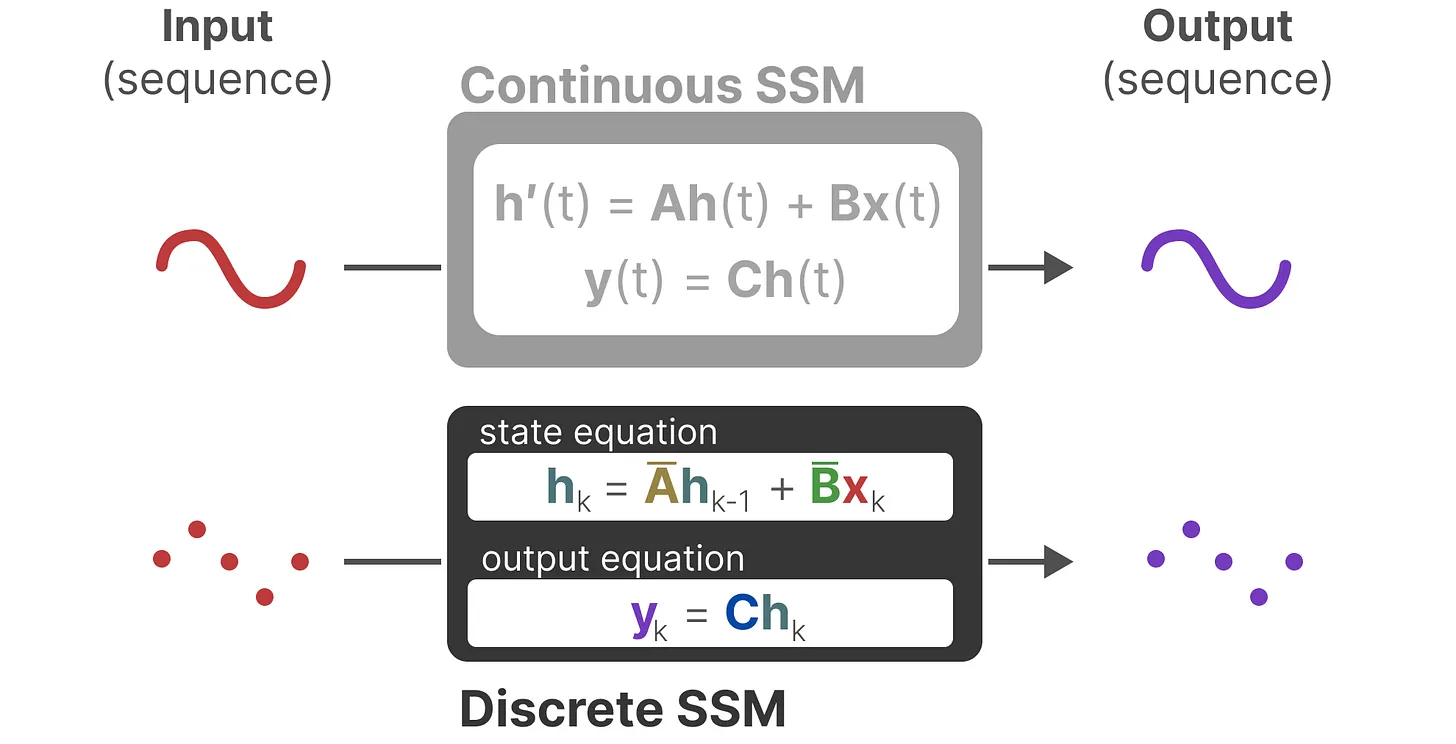
SSMs假设动态系统（如 3D 空间中移动的物体），可以通过下面两个方程对其在时间 \(t\) 的状态进行预测。

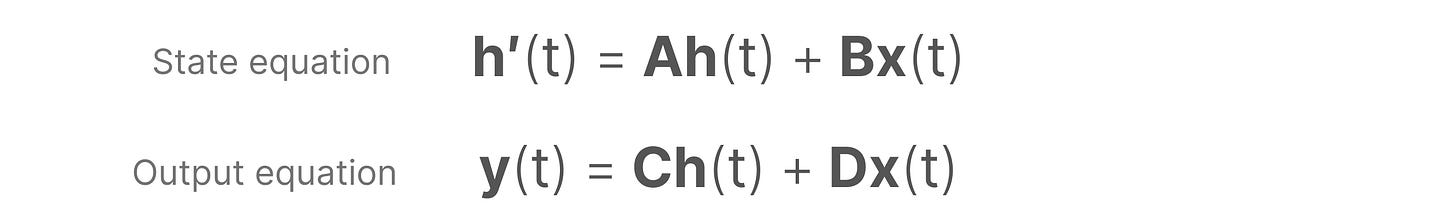
我们希望通过数学方程，把系统的历史状态和输入信号，转换成一种“状态表示” \(h(t)\)。有了这个 \(h(t)\)，我们就能根据输入信号，预测系统接下来会怎么变化、会输出什么结果。

这两个方程是状态空间模型的核心。其中，\(h(t)\) 指的是在任意给定时间 \(t\) 的潜在状态表示，而 \(x(t)\)指的是某些输入。

状态方程
输出方程描述了状态是如何通过矩阵 C 转换为输出，以及输入是如何通过矩阵 D 影响输出的。这里同样有两个重要的矩阵

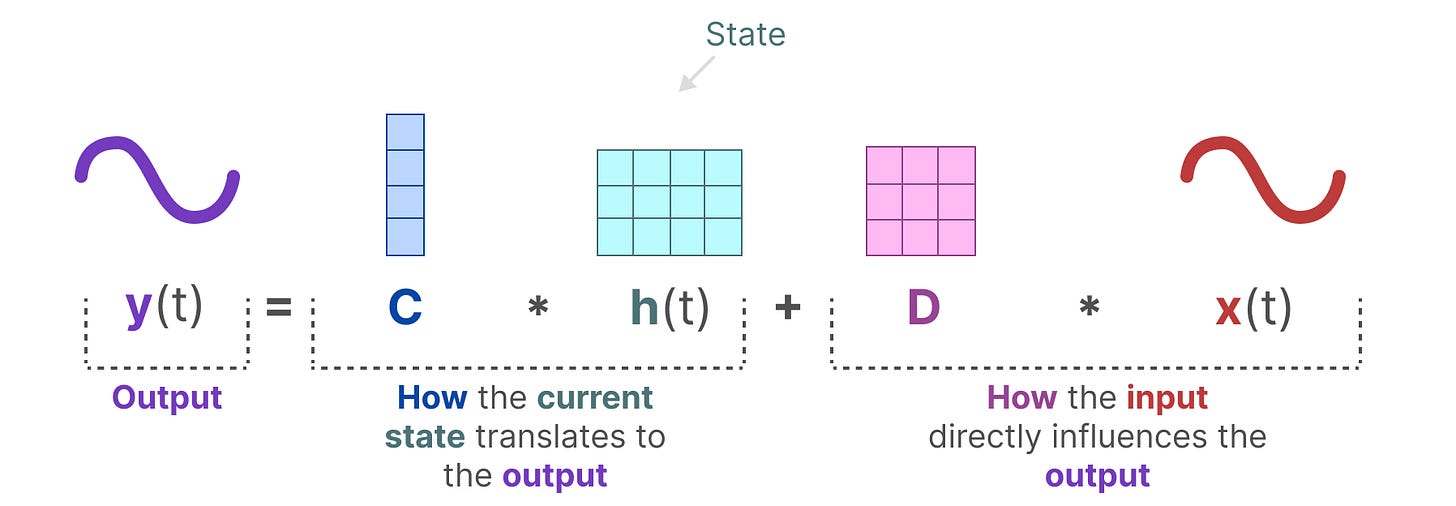
状态空间模型架构

可视化这两个方程，我们得到以下架构：

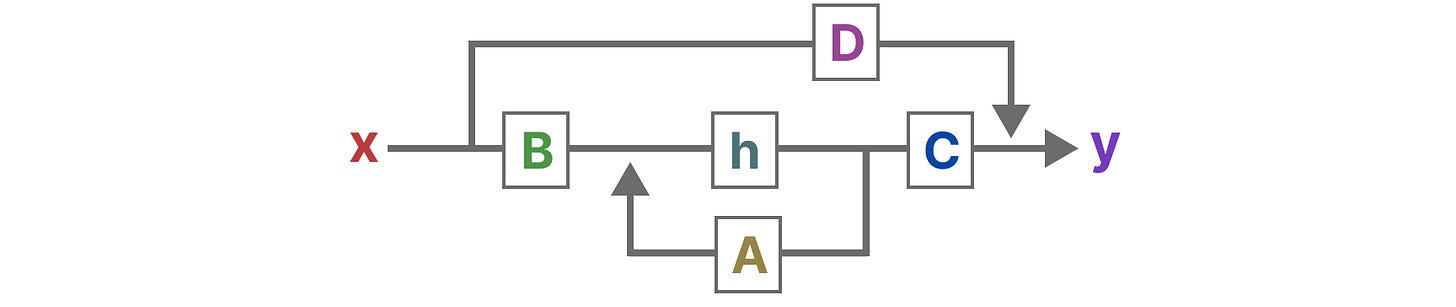
让我们一步一步地了解这些矩阵如何影响学习过程。

假设我们有一些输入信号 x(t)，这个信号首先被矩阵 \(B\) 乘以，该矩阵描述了输入如何影响系统。
更新后的状态（类似于神经网络的隐藏状态）是一个包含环境核心“知识”的潜在空间。我们用矩阵 A 乘以状态，矩阵 A 描述了所有内部状态如何连接，因为它们代表了系统的潜在动态。
然后，我们使用矩阵 C 来描述状态如何转换为输出。
最后，我们可以利用矩阵 \(D\) 直接从输入到输出提供信号。这通常也被称为残差连接。
SSM 通常被视为以下形式，而不包含残差连接。

从连续信号到离散信号

在自然界或许多工程系统中，信号随时间连续变化（如温度、速度等）。但在实际应用（如文本序列、数字采样）中，我们通常只在特定时刻获得输入数据。如果系统模型（如状态空间模型，SSM）是连续的，而输入却是离散的，那么直接分析和计算就很困难。

为了做到这一点，我们使用零阶保持（Zero-order hold ）技术。它把离散输入“变成”连续信号，使得连续时间的模型可以处理。具体来说，每当收到一个新的离散输入，就把这个值“保持”到下一个输入到来为止。这样得到一个阶梯状的连续信号，如下图所示

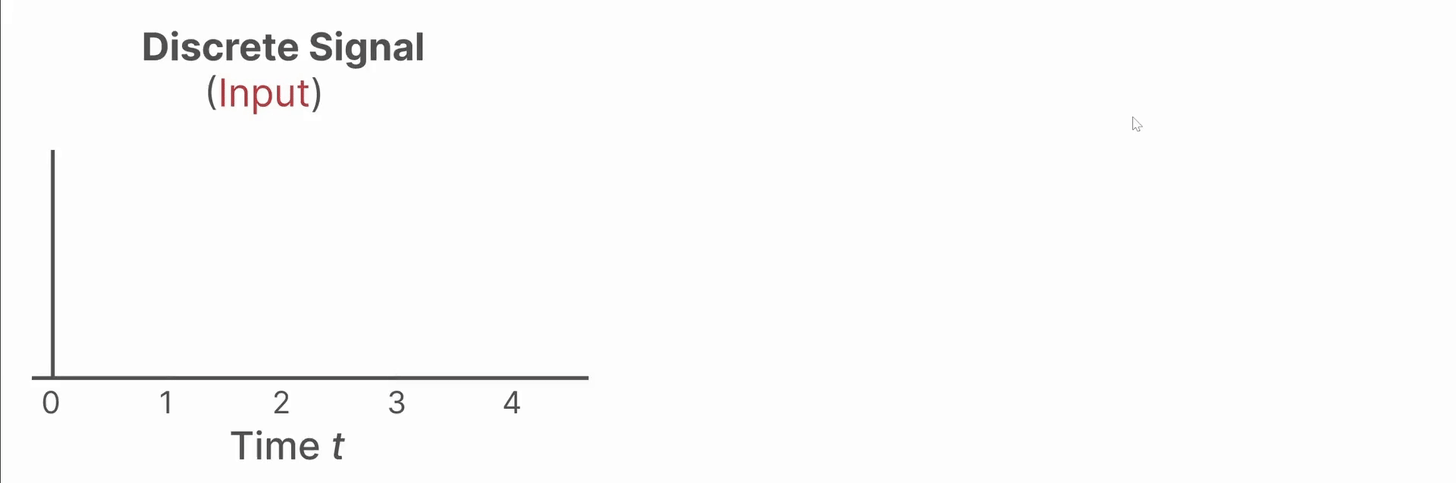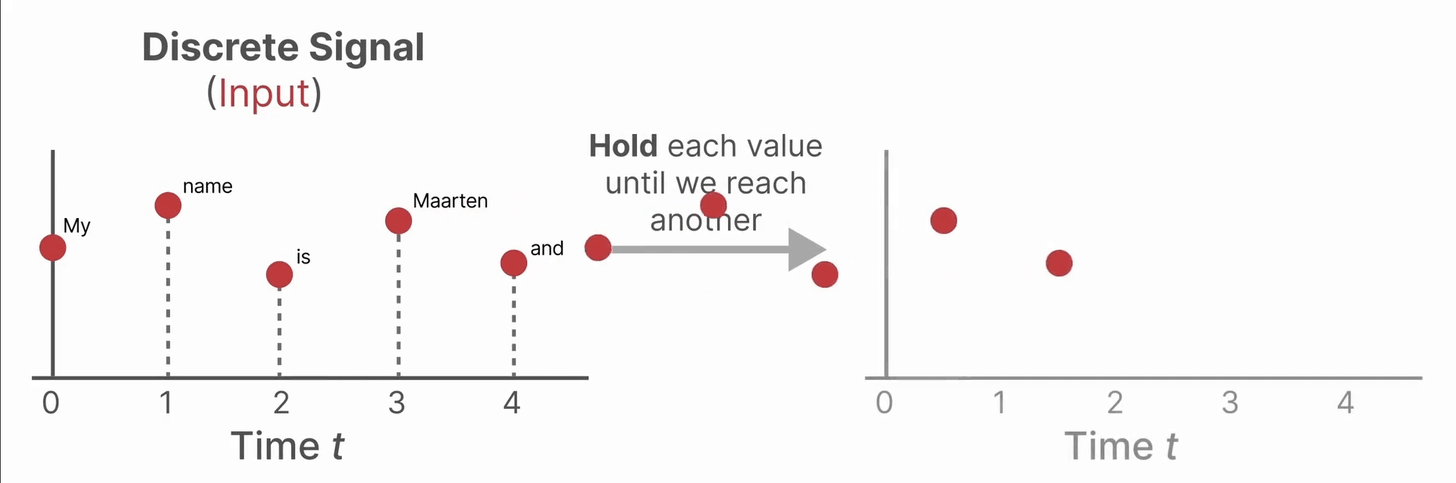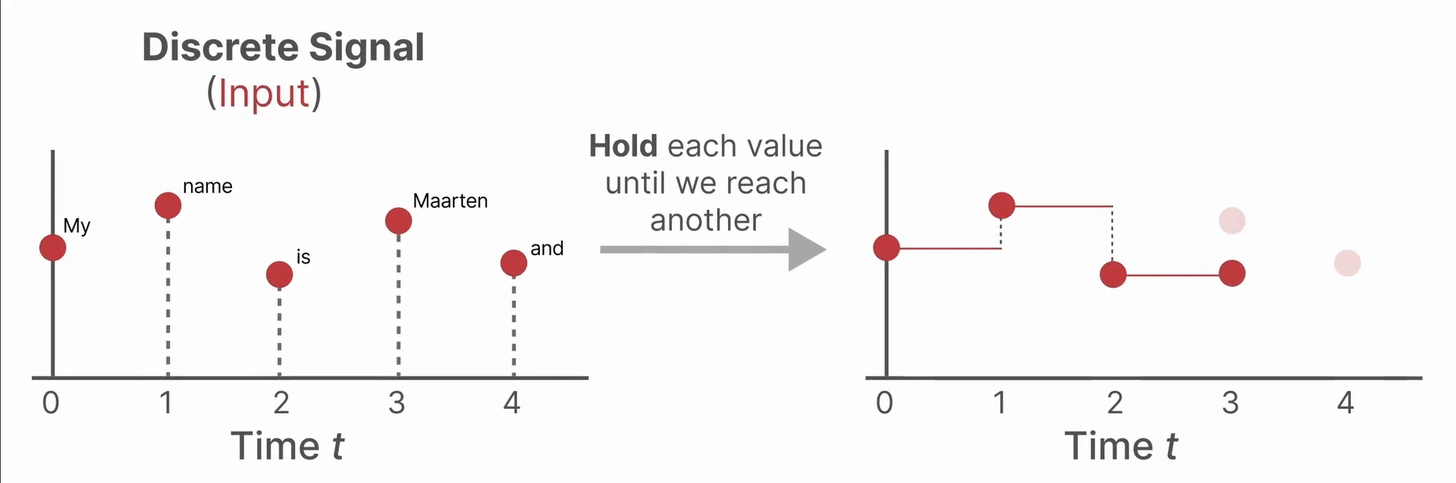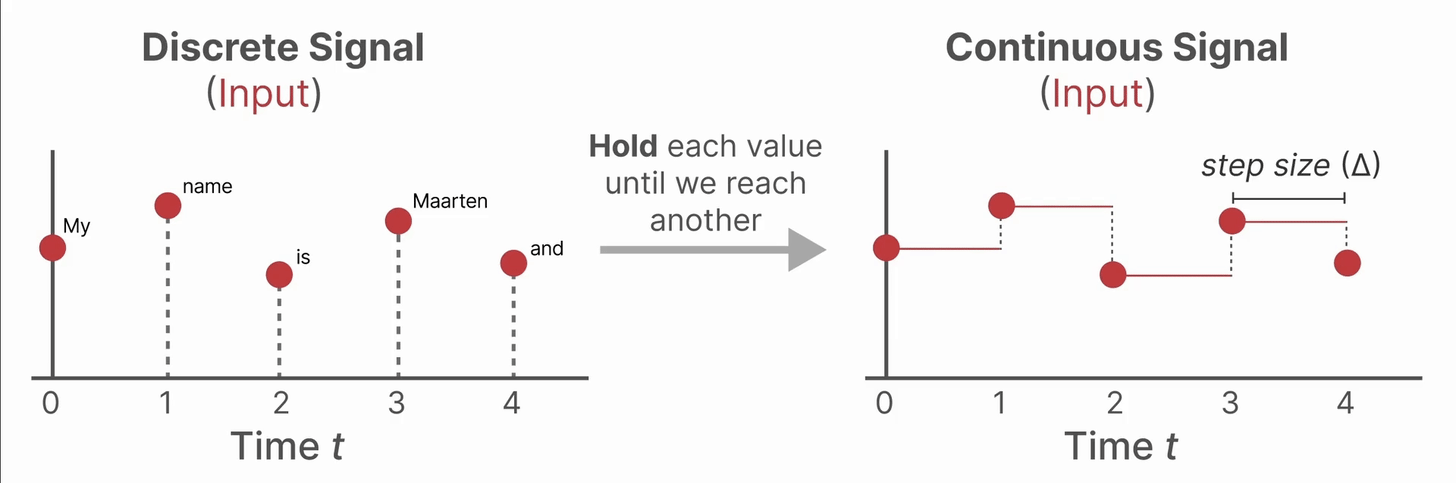
保持每个输入值的时间长度称为“步长”，记作 \(\Delta\)。决定了离散化的“分辨率”，也可以设为可学习的参数，让模型自动适应最优的采样频率。

现在我们有了连续的输入信号，我们可以生成连续的输出，对于输出可以根据输入的时间步长采样就变成了离散的输出。

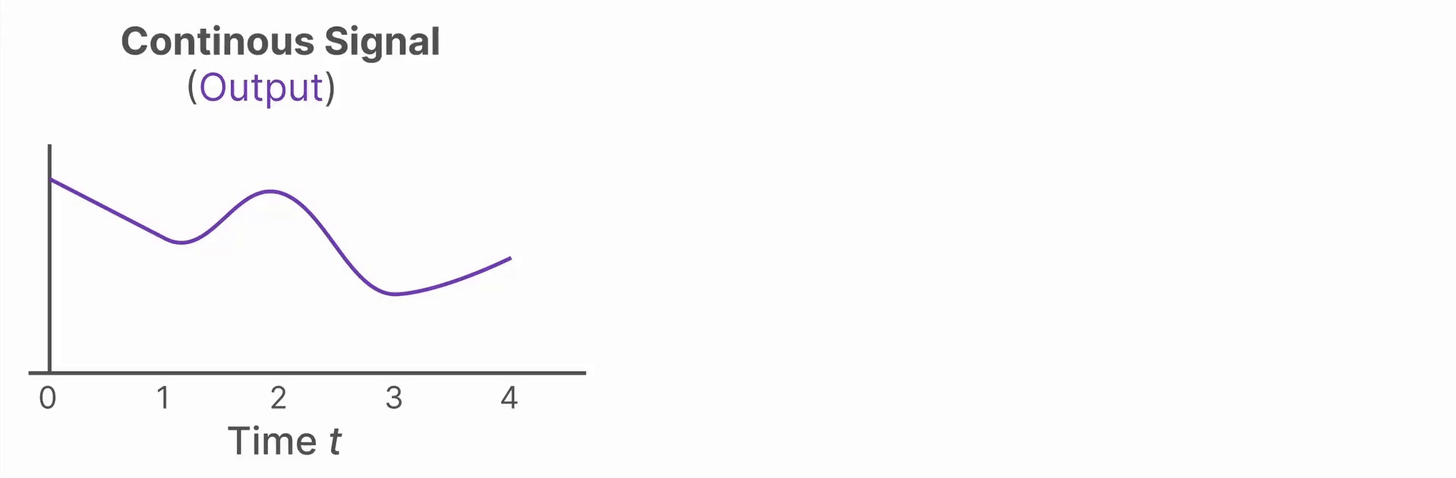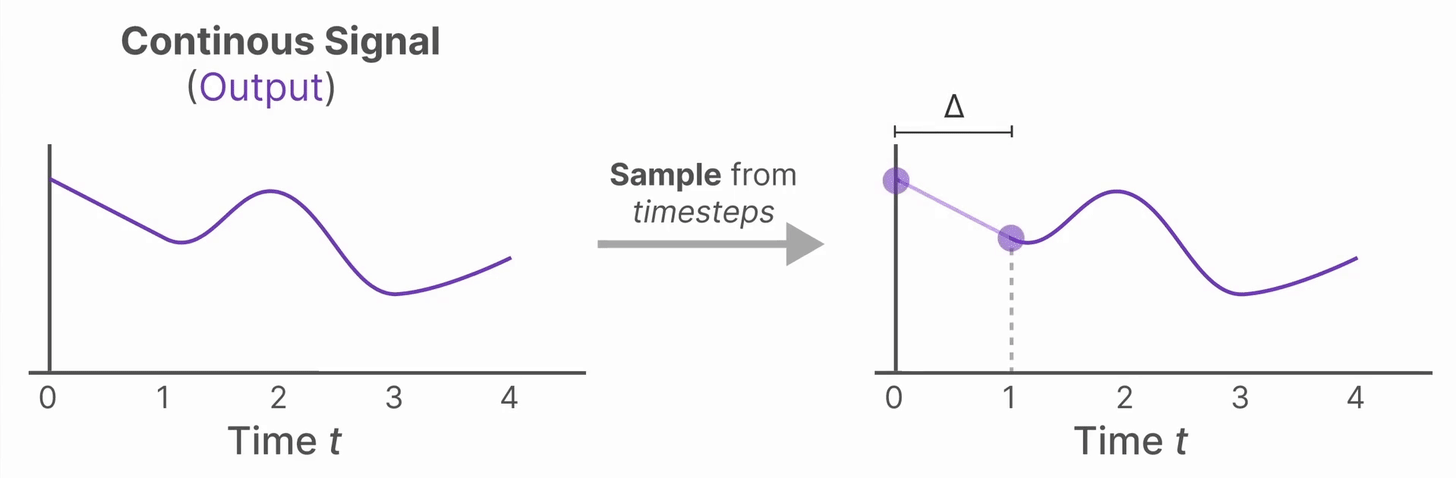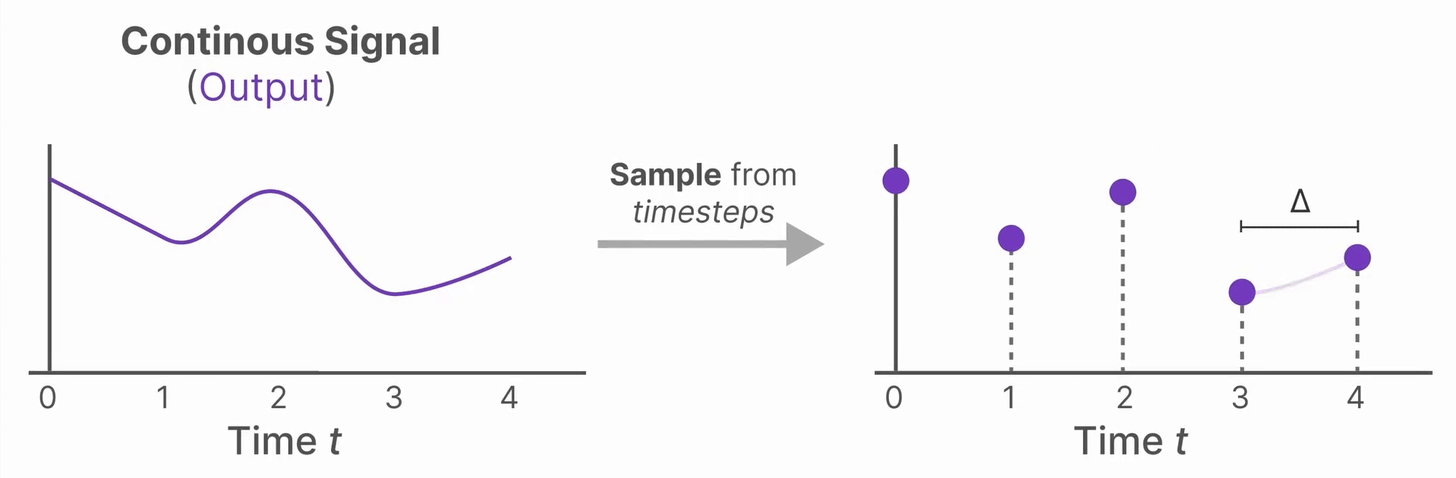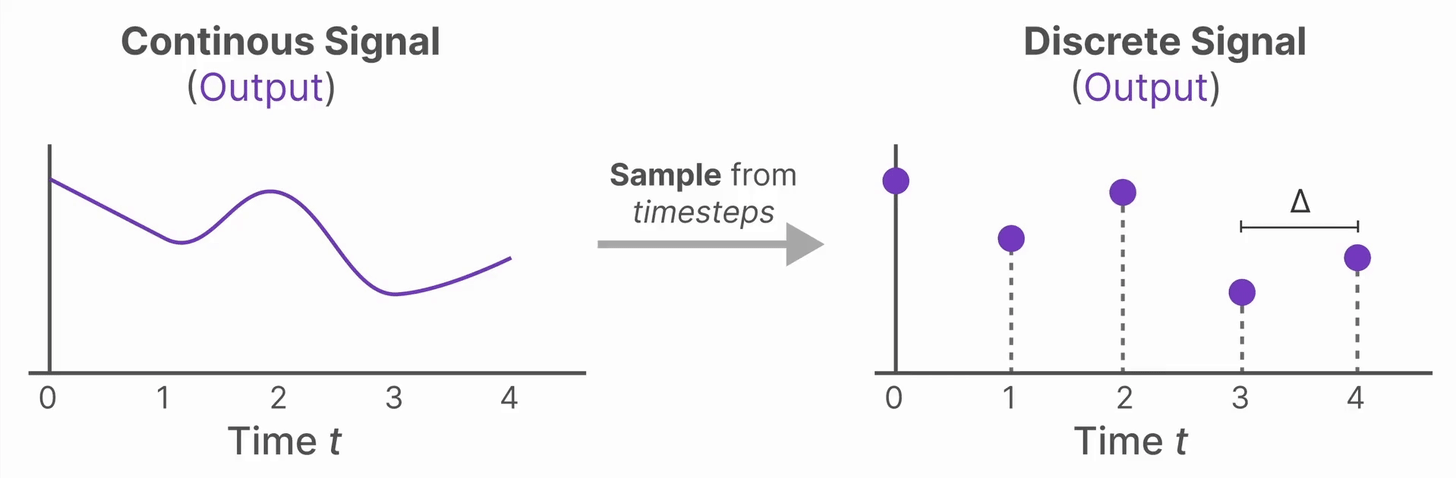
从数学上讲，我们可以将零阶保持应用到状态转移矩阵 \(A\) 和输入矩阵 \(B\) 也需要离散化，变成适用于离散时间的参数。

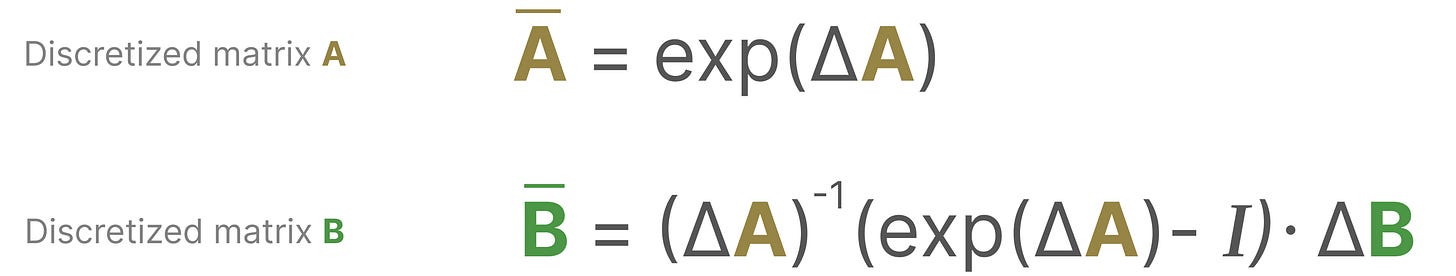
原本是 \(x(t) \rightarrow y(t)\)，即输入和输出都是时间的连续函数。现在我们通过Zero-order hold，把输入和输出都变成了序列 \(x_k \rightarrow y_k\)，\(k\) 表示离散时间步。

矩阵 A 的重要性

毫无疑问，SSM 公式的最重要方面之一是矩阵 A。它捕捉了先前的状态信息以构建新的状态。

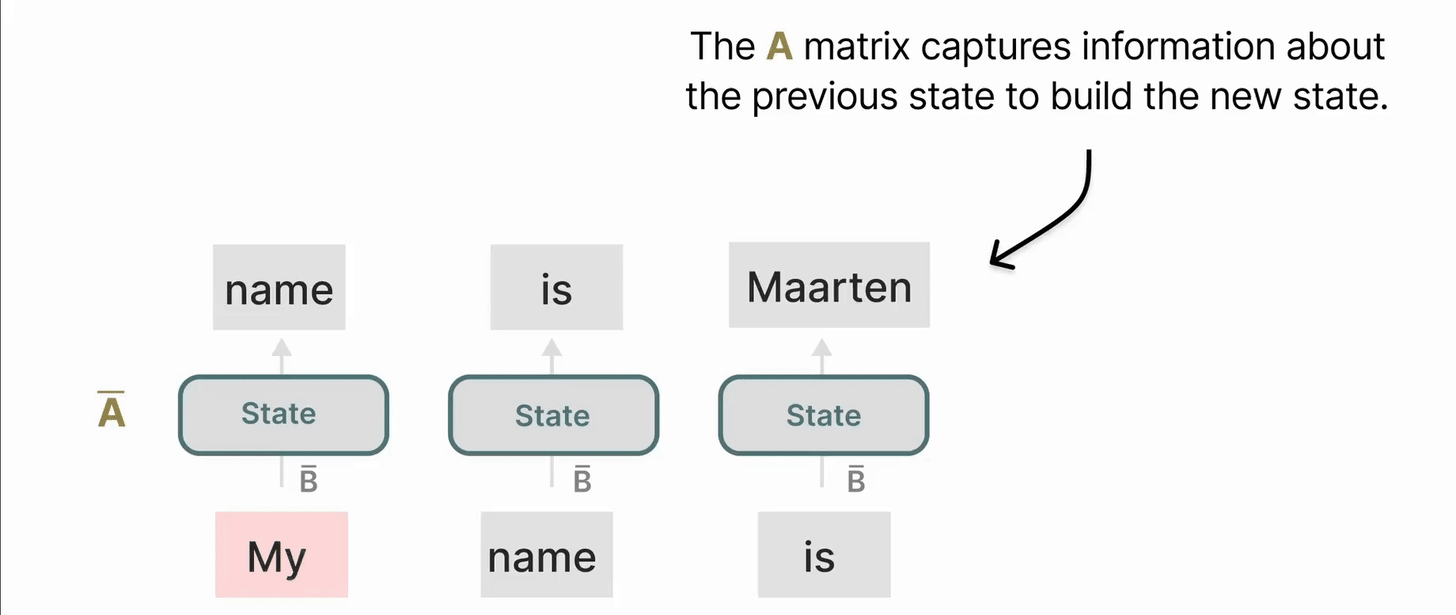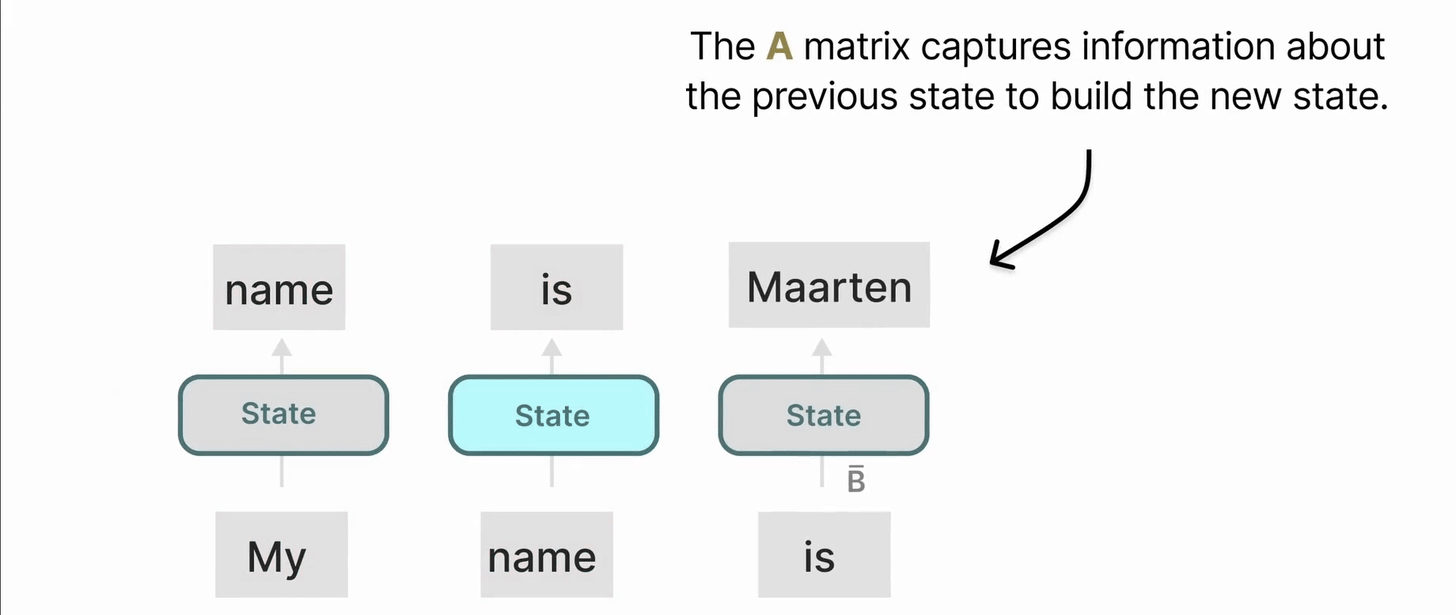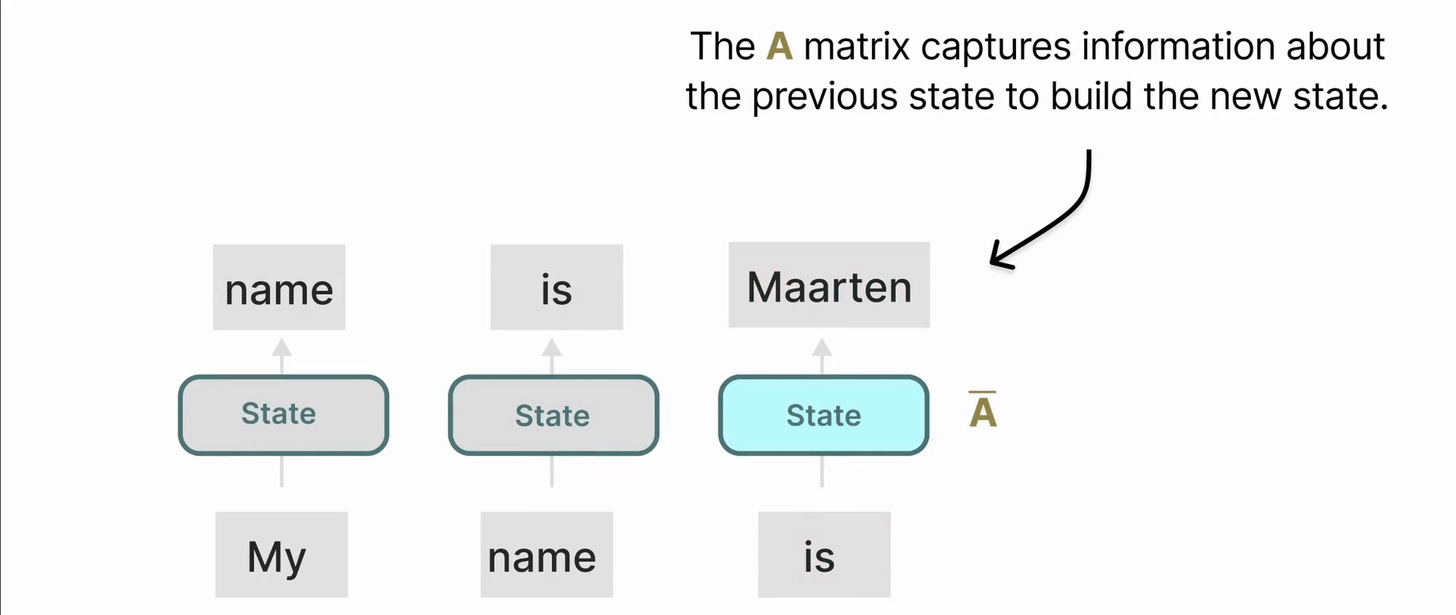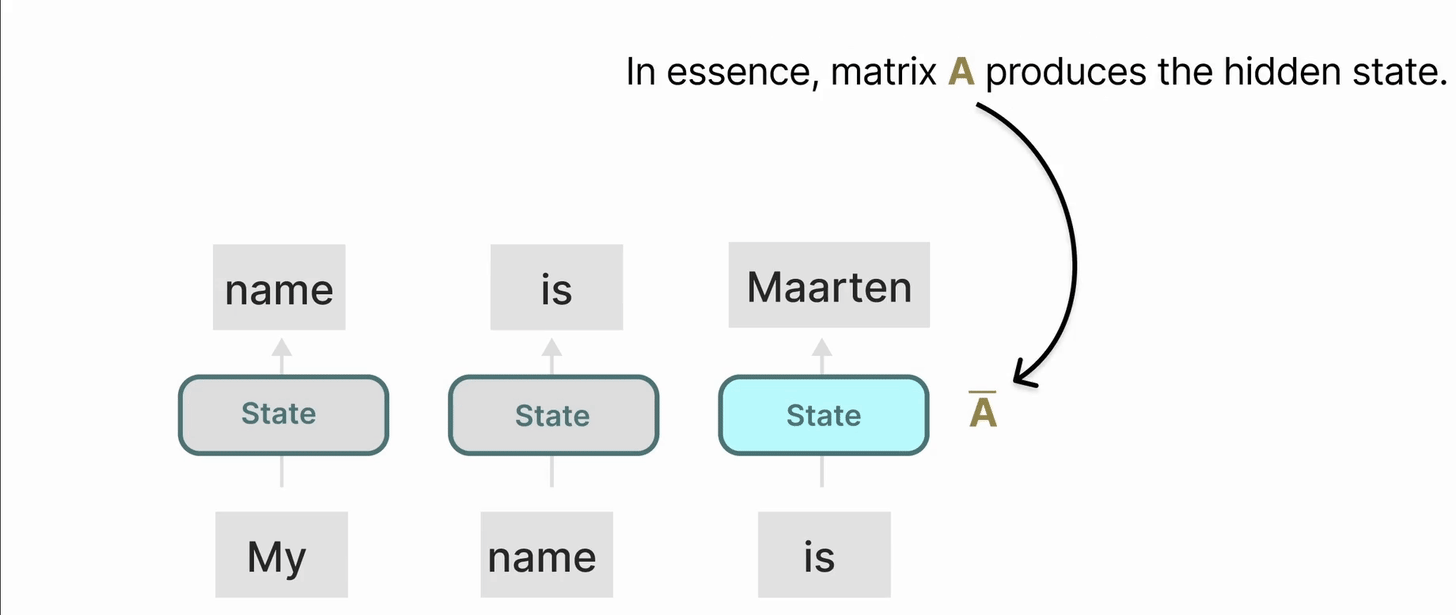
从本质上讲，矩阵 A 产生了隐藏状态：

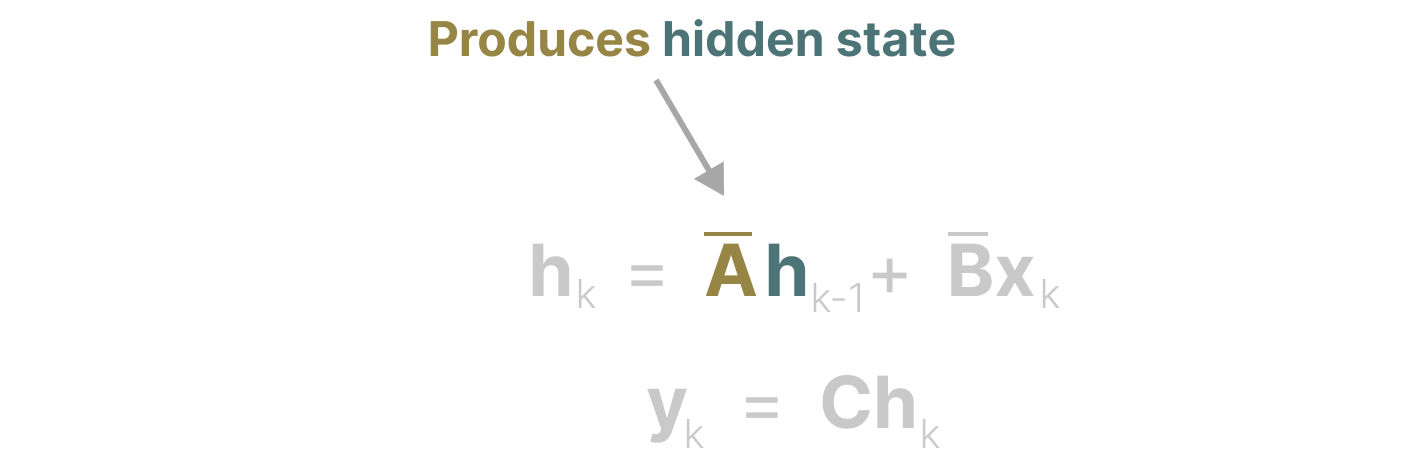
矩阵 \(A\) 决定了当前状态如何由前一个状态演化而来。\(A\) 的设计直接影响了模型对历史信息的“记忆长度”和“记忆方式”。

如果 \(A\) 设计得比较“短视”，比如只有最近的几个状态有影响，那么模型只能记住最近的几个 token（输入）。
如果 \(A\) 设计得“长视”或者有特殊结构（比如对角化、低秩、带有遗忘门等），就可能让模型把所有历史 token的信息都融入到当前状态中，实现“长时记忆”。
总的来说，\(A\) 决定了模型记忆历史的能力。那么我们如何创建矩阵 \(A\) 以保留大量记忆（上下文大小）呢？

HiPPO

我们可以使用HIPPO，即高阶多项式投影算子。HiPPO 试图将其迄今为止看到的所有输入信号压缩成一个系数向量。

详情可以可以参考：

S4(Structured State Space for Sequences)

S4是对HiPPO的进一步补充和完成，它的关键一笔是提出了 \(A\) 等价于“对角+低秩”的矩阵形式，为剩余部分的分析奠定了基础。因为一开始 \(A\) 是分段定义的形式，而不是矩阵运算形式，这样的定义不利于应用现有的线性代数工具进行一般化分析。

S4 是一种最近出现的状态空间模型（SSM）架构。在这里，只是总结其中的重要部分，但如果想要更深入地了解 S4，可以阅读https://kexue.fm/archives/10162 和 https://srush.github.io/annotated-s4/

从高层次来看，S4 学习如何通过一个中间状态 \(h(t)\) 将输入 \(x(t)\) 映射到输出 \(y(t)\) 。在这里， \(x\) 、 \(y\) 和 \(h\) 是 \(t\) 的函数，因为 SSM 被设计成连续数据（如音频、传感器数据和图像）可以比较好的工作。S4 通过三个连续参数矩阵 \(A\) 、 \(B\) 和 \(C\) 将它们联系起来。这些参数通过以下两个方程相互关联：

\[ \begin{aligned}h'(t)&=\mathbf{A}h(t)+\mathbf{B}x(t)\\y(t)&=\mathbf{C}h(t)\end{aligned} \]

在实践中，我们总是处理离散数据，如文本。这需要我们将 SSM 离散化，通过使用

\(Δ\)将连续参数 \(\mathbf{A}\)，\(\mathbf{B}\)，\(\mathbf{C}\) 转换为离散参数 \(\mathbf{\bar{A}}\)，\(\mathbf{\bar{B}}\)，\(\mathbf{C}\)。一旦离散化，我们就可以通过以下两个方程来表示 SSM：

\[ \begin{aligned}h_t&=\mathbf{\bar{A}}h_{t-1}+\mathbf{\bar{B}}x_t\\y_t&=\mathbf{C}h_t\end{aligned} \]

这些方程构成了一个递归，类似于在循环神经网络（RNN）。在每一步 \(t\) ，我们将前一个时间步的隐藏状态 \(h_{t−1}\) 与当前输入 \(x_t\) 结合，以创建新的隐藏状态 \(h_t\) 。下面这张图显示了如何预测句子中的下一个单词（在这种情况下，预测“and”跟在“My name is Jack”后面）。

以这种方式，我们实际上可以将 S4 作为 RNN 一次生成一个标记。然而，S4 真正酷的地方在于你还可以将其用作卷积神经网络（CNN）。在上面的例子中，让我们看看当我们把之前提到的离散方程扩展到尝试计算 \(h_3\) 时会发生什么。为了简单起见，让我们假设 \(x_{−1}=0\) 。

\[ \begin{aligned}h_0&=\mathbf{\bar{B}}x_0\\h_1&=\mathbf{\bar{A}}(\mathbf{\bar{B}}x_0)+\mathbf{\bar{B}}x_1\\h_2&=\mathbf{\bar{A}}(\mathbf{\bar{A}}(\mathbf{\bar{B}}x_0)+\mathbf{\bar{B}}x_1)+\mathbf{\bar{B}}x_2\\h_3&=\mathbf{\bar{A}}(\mathbf{\bar{A}}(\mathbf{\bar{A}}(\mathbf{\bar{B}}x_0)+\mathbf{\bar{B}}x_1)+\mathbf{\bar{B}}x_2)+\mathbf{\bar{B}}x_3\end{aligned} \]

计算 \(h_3\) 后，我们可以将其代入 \(y_3\) 的方程中，以预测下一个单词。

\[ \begin{aligned}y_3&=\mathbf{C}(\mathbf{\bar{A}}(\mathbf{\bar{A}}(\mathbf{\bar{A}}(\mathbf{\bar{B}}x_0)+\mathbf{\bar{B}}x_1)+\mathbf{\bar{B}}x_2)+\mathbf{\bar{B}}x_3)\\y_3&=\mathbf{C\bar{A}\bar{A}\bar{A}\bar{B}}x_0+\mathbf{C\bar{A}\bar{A}\bar{B}}x_1+\mathbf{C\bar{A}\bar{B}}x_2+\mathbf{C\bar{B}}x_3\end{aligned} \]

注意到， \(y_3\) 实际上可以计算为一个点积，其中右边的向量只是我们的输入 \(x\) ：

\[ y_3=\begin{pmatrix}\mathbf{C\bar{A}\bar{A}\bar{A}\bar{B}} & \mathbf{C\bar{A}\bar{A}\bar{B}} & \mathbf{C\bar{A}\bar{B}} & \mathbf{C\bar{B}}\end{pmatrix}\begin{pmatrix}x_0\\x_1\\x_2\\x_3\end{pmatrix} \]

因为 \(\mathbf{\bar{A}}\)， \(\mathbf{\bar{B}}\) 和 \(\mathbf{C}\) 都是常数，我们可以预先计算左端向量并将其保存为我们的卷积核 \(\mathbf{\bar{K}}\) 。这使得我们能够通过以下两个方程轻松地通过卷积计算 \(y\) ：

\[ \begin{aligned}\mathbf{\bar{K}}&=\begin{pmatrix}\mathbf{C\bar{B}} & \mathbf{C\bar{A}\bar{B}} & \cdots & \mathbf{C\bar{A}^k\bar{B}}\end{pmatrix}\\y&=\mathbf{\bar{K}} * x\end{aligned} \]

重要的是，“RNN 模式”和“CNN 模式”，在数学上是等价的。这使得 S4 可以根据需要执行的任务进行变形，其输出没有差异。我们可以在 S4 论文的表 1 中比较这些“模式”之间的差异，该表显示了每种形式的训练和推理的运行时复杂度（粗体表示每个指标的最佳结果）。

可以注意到 CNN 模式更适合训练，而 RNN 模式更适合推理。在 CNN 模式下，我们可以利用并行性一次性训练多个示例。在 RNN 模式下，尽管我们一次只能计算一步，但每一步都需要相同的工作量。因为 S4 可以使用这两种模式，所以它实际上得到了两者的最佳结合：快速训练，以及更快的推理。

Mamba

现在我们可以探讨 Mamba 提出的第一个主要观点：选择性。让我们回顾一下定义 S4 离散形式的两个方程：

\[ \begin{aligned}h_t&=\mathbf{\bar{A}}h_{t-1}+\mathbf{\bar{B}}x_t\\y_t&=\mathbf{C}h_t\end{aligned} \]

选择性

请注意，在 S4 中，离散参数 \(\mathbf{\bar{A}}\)， \(\mathbf{\bar{B}}\) 和 \(\mathbf{C}\) 是常数。然而，Mamba 使这些参数根据输入而变化。我们最终会得到类似以下的内容：

\[ \begin{aligned}h_t&=s_\mathbf{\bar{A}}(x_t)h_{t-1}+s_\mathbf{\bar{B}}(x_t)x_t\\y_t&=s_\mathbf{C}(x_t)h_t\end{aligned} \]

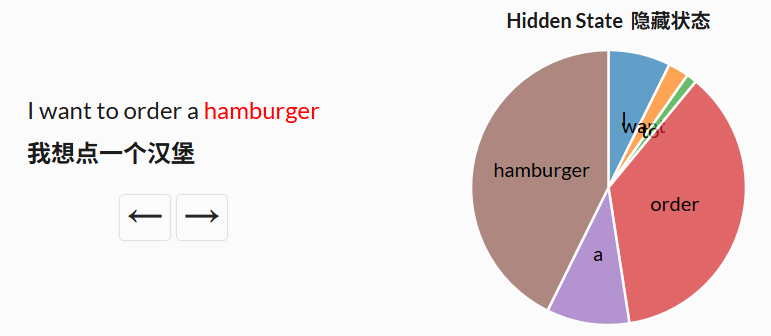
作者认为选择性，或者说输入依赖性，对于许多任务来说很重要。可以这样思考：因为 S4 没有选择性，它被迫对输入的所有部分进行完全相同的处理。然而，当你阅读一个句子时，一些词不可避免地比其他词更重要。想象一下，我们有一个根据意图对句子进行分类的模型，我们给它提供的句子是：“我想点一个汉堡。”如果没有选择性，S4 在处理每个词时都会花费相同的“努力”。点击下面的按钮，看看句子是如何逐个词被处理的。

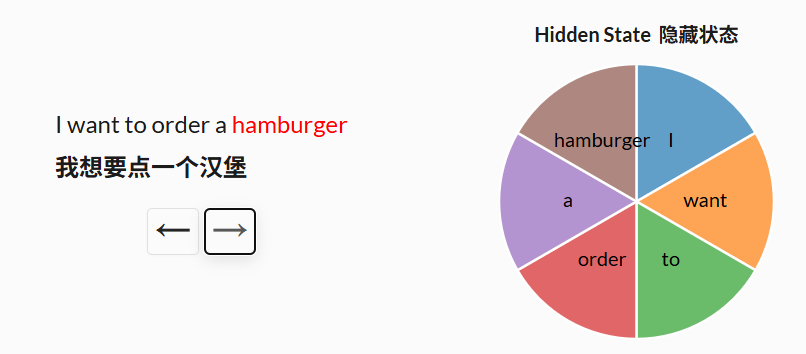
但如果你是一个试图分类句子意图的模型，你可能更希望“关注”一些词而不是其他词。单词“想要”和“要”在句子的潜在含义中真正贡献了多少价值？实际上，如果我们能更多地用有限的脑力关注像“订单”这样的词，以了解用户想要做什么，以及“汉堡”这样的词，以了解用户在点什么，那就太好了。通过使模型参数成为输入的函数，Mamba 使得关注对当前任务更重要的输入部分成为可能。

然而，选择性给我们带来了问题。让我们回顾一下我们之前计算的卷积核 \(\mathbf{\bar{K}}\)