PCA原理总结

PCA的思想

PCA顾名思义，就是找出数据里最主要的方面，用数据里最主要的方面来代替原始数据。具体的，假如我们的数据集是n维的，共有m个数据\((𝑥(1),𝑥(2),...,𝑥(𝑚))\)。我们希望将这m个数据的维度从n维降到n'维，希望这m个n'维的数据集尽可能的代表原始数据集。我们知道数据从n维降到n'维肯定会有损失，但是我们希望损失尽可能的小。那么如何让这n'维的数据尽可能表示原来的数据呢？

我们先看看最简单的情况，也就是n=2，n'=1,也就是将数据从二维降维到一维。数据如下图。我们希望找到某一个维度方向，它可以代表这两个维度的数据。图中列了两个向量方向，\(u_1\)和\(𝑢_2\)，那么哪个向量可以更好的代表原始数据集呢？从直观上也可以看出，\(𝑢_1\)比\(𝑢_2\)好。

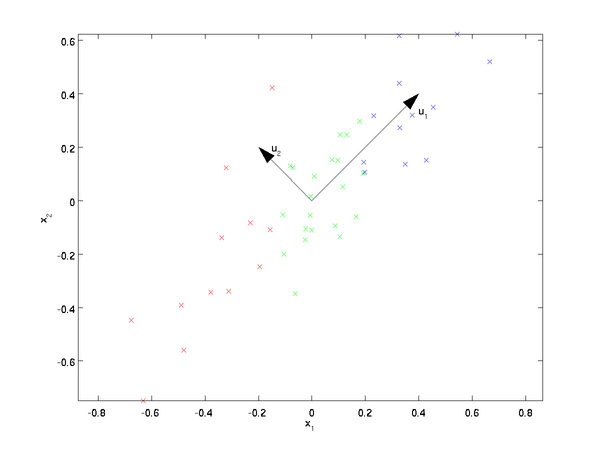
为什么\(𝑢_1\)比\(𝑢_2\)好呢？可以有两种解释，第一种解释是样本点到这个直线的距离足够近，第二种解释是样本点在这个直线上的投影能尽可能的分开。

假如我们把n'从1维推广到任意维，则我们的希望降维的标准为：样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。

基于上面的两种标准，我们可以得到PCA的两种等价推导。

PCA的推导:基于最小投影距离

我们首先看第一种解释的推导，即样本点到这个超平面的距离足够近。

假设m个n维数据\((𝑥^{(1)},𝑥^{(2)},...,𝑥^{(𝑚)})\)都已经进行了中心化，即\(∑_{𝑖=1}^𝑚𝑥^{(𝑖)}=0\)。经过投影变换后得到的新坐标系为\(\{𝑤_1,𝑤_2,...,𝑤_𝑛\}\),其中𝑤 是标准正交基，即\(||𝑤||^2=1,𝑤^𝑇_𝑖𝑤_𝑗=0\)。

如果我们将数据从n维降到n'维，即丢弃新坐标系中的部分坐标，则新的坐标系为\(\{𝑤_1,𝑤_2,...,𝑤_{𝑛^′}\}\),样本点\(𝑥^{(𝑖)}\)在n'维坐标系中的投影为：\(𝑧^{(𝑖)}=(𝑧^{(𝑖)}_1,𝑧^{(𝑖)}_2,...,𝑧^{(𝑖)}_{𝑛^′})^𝑇\).其中，\(𝑧^{(𝑖)}_𝑗=𝑤^𝑇_𝑗𝑥^{(𝑖)}\)是\(𝑥^{(𝑖)}\)在低维坐标系里第j维的坐标。

如果我们用\(𝑧^{(𝑖)}\)来恢复原始数据\(𝑥^{(𝑖)}\),则得到的恢复数据 \(\overline{x}^{(i)}=∑_{j=1}^{n^′}z_j^{(i)}w_j=Wz^{(i)}\),其中，\(W\)为标准正交基组成的矩阵。

现在我们考虑整个样本集，我们希望所有的样本到这个超平面的距离足够近，即最小化下式：

\[ \sum\limits_{i=1}^{m}||\overline{x}^{(i)} - x^{(i)}||_2^2 \]

将这个式子进行整理，可以得到:

\[ \begin{aligned} \sum\limits_{i=1}^{m}||\overline{x}^{(i)} - x^{(i)}||_2^2 & = \sum\limits_{i=1}^{m}|| Wz^{(i)} - x^{(i)}||_2^2 \\& = \sum\limits_{i=1}^{m}(Wz^{(i)})^T(Wz^{(i)}) - 2\sum\limits_{i=1}^{m}(Wz^{(i)})^Tx^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}W^Tx^{(i)} +\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}z^{(i)}+\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = - \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = -tr( W^T（\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T})W) + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = -tr( W^TXX^TW) + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \end{aligned} \]

其中第（1）步用到了\(\overline{x}^{(i)}=Wz^{(i)}\),第二步用到了平方和展开，第（3）步用到了矩阵转置公式,第（4）步用到了\(z^{(i)}=W^Tx^{(i)}\)，第（5）步合并同类项，第（6）步用到了𝑧(𝑖)=𝑊𝑇𝑥(𝑖)z(i)=WTx(i)和矩阵的迹,第7步将代数和表达为矩阵形式。

注意到\(\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}\)是数据集的协方差矩阵，\(W\)的每一个向量\(𝑤_𝑗\)是标准正交基。而\(\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)}\)是一个常量。最小化上式等价于：

\[ \underbrace{arg\;min}_{W}\;-tr( W^TXX^TW) \;\;s.t. W^TW=I \]

这个最小化不难，直接观察也可以发现最小值对应的W由协方差矩阵\(𝑋𝑋^𝑇\)最大的n'个特征值对应的特征向量组成。当然用数学推导也很容易。利用拉格朗日函数可以得到

\[ J(W) = -tr( W^TXX^TW + \lambda(W^TW-I)) \]

对W求导有\(−𝑋𝑋^𝑇𝑊+\lambda𝑊=0\), 整理下即为：

\[ XX^TW=\lambda W \]

这样可以更清楚的看出，\(W\)为\(XX^T\)的n'个特征向量组成的矩阵，而\(λ\)为\(XX^T\)的若干特征值组成的矩阵，特征值在主对角线上，其余位置为0。当我们将数据集从n维降到n'维时，需要找到最大的n'个特征值对应的特征向量。这n'个特征向量组成的矩阵W即为我们需要的矩阵。对于原始数据集，我们只需要用\(𝑧^{(𝑖)}=𝑊^𝑇𝑥^{(𝑖)}\),就可以把原始数据集降维到最小投影距离的n'维数据集。

如果你熟悉谱聚类的优化过程，就会发现和PCA的非常类似，只不过谱聚类是求前k个最小的特征值对应的特征向量，而PCA是求前k个最大的特征值对应的特征向量。

PCA的推导:基于最大投影方差

现在我们再来看看基于最大投影方差的推导。

对于任意一个样本\(𝑥^{(𝑖)}\)，在新的坐标系中的投影为\(𝑊^𝑇𝑥^{(𝑖)}\),在新坐标系中的投影方差为\(𝑥^{(𝑖)𝑇}𝑊𝑊^𝑇𝑥^{(𝑖)}\)，要使所有的样本的投影方差和最大，也就是最大化\(\sum\limits_{i=1}^{m}W^Tx^{(i)}x^{(i)T}W\)的迹,即：

\[ \underbrace{arg\;max}_{W}\;tr( W^TXX^TW) \;\;s.t. W^TW=I \]

观察第二节的基于最小投影距离的优化目标，可以发现完全一样，只是一个是加负号的最小化，一个是最大化。

利用拉格朗日函数可以得到

\[ J(W) = tr( W^TXX^TW + \lambda(W^TW-I)) \]

对W求导有\(𝑋𝑋^𝑇𝑊+\lambda𝑊=0\), 整理下即为：

\[ XX^TW=（-\lambda）W \]

和上面一样可以看出，\(W\)为\(𝑋𝑋^𝑇\)的n'个特征向量组成的矩阵，而−λ为\(𝑋𝑋^𝑇\)的若干特征值组成的矩阵，特征值在主对角线上，其余位置为0。当我们将数据集从n维降到n'维时，需要找到最大的n'个特征值对应的特征向量。这n'个特征向量组成的矩阵W即为我们需要的矩阵。对于原始数据集，我们只需要用\(z^{(i)}=W^Tx^{(i)}\),就可以把原始数据集降维到最小投影距离的n'维数据集。

PCA算法流程

从上面两节我们可以看出，求样本\(𝑥^{(𝑖)}\)的n'维的主成分其实就是求样本集的协方差矩阵\(𝑋𝑋^𝑇\)的前n'个特征值对应特征向量矩阵W，然后对于每个样本\(𝑥^{(𝑖)}\),做如下变换\(𝑧^{(𝑖)}=𝑊^𝑇𝑥^{(𝑖)}\)，即达到降维的PCA目的。

下面我们看看具体的算法流程。

输入：n维样本集\(𝐷=(𝑥^{(1)},𝑥^{(2)},...,𝑥^{(𝑚)})\)，要降维到的维数n'.

输出：降维后的样本集𝐷′

1) 对所有的样本进行中心化： \(x^{(i)}=x^{(i)}−\frac{1}{m}∑_{j=1}^mx^{(j)}\)

2) 计算样本的协方差矩阵\(𝑋𝑋^𝑇\)

3) 对矩阵\(𝑋𝑋^𝑇\)进行特征值分解

4）取出最大的n'个特征值对应的特征向量\((𝑤_1,𝑤_2,...,𝑤_{𝑛^{′}})\), 将所有的特征向量标准化后，组成特征向量矩阵W。

5）对样本集中的每一个样本\(𝑥^{(𝑖)}\),转化为新的样本\(𝑧^{(𝑖)}=𝑊^𝑇𝑥^{(𝑖)}\)

6) 得到输出样本集\(𝐷^{′}=(𝑧^{(1)},𝑧^{(2)},...,𝑧^{(𝑚)})\)

有时候，我们不指定降维后的n'的值，而是换种方式，指定一个降维到的主成分比重阈值t。这个阈值t在（0,1]之间。假如我们的n个特征值为\(\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_n\),则n'可以通过下式得到:

\[ \frac{\sum\limits_{i=1}^{n'}\lambda_i}{\sum\limits_{i=1}^{n}\lambda_i} \geq t \]

PCA实例

下面举一个简单的例子，说明PCA的过程。

假设我们的数据集有10个二维数据(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0), (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9)，需要用PCA降到1维特征。

首先我们对样本中心化，这里样本的均值为(1.81, 1.91),所有的样本减去这个均值向量后，即中心化后的数据集为(0.69, 0.49), (-1.31, -1.21), (0.39, 0.99), (0.09, 0.29), (1.29, 1.09), (0.49, 0.79), (0.19, -0.31), (-0.81, -0.81), (-0.31, -0.31), (-0.71, -1.01)。

现在我们开始求样本的协方差矩阵，由于我们是二维的，则协方差矩阵为：

\[ \mathbf{XX^T} = \left( \begin{array}{ccc} cov(x_1,x_1) & cov(x_1,x_2)\\ cov(x_2,x_1) & cov(x_2,x_2) \end{array} \right) \]

对于我们的数据，求出协方差矩阵为：

\[ \mathbf{XX^T} = \left( \begin{array}{ccc} 0.616555556 & 0.615444444\\ 0.615444444 & 0.716555556 \end{array} \right) \]

求出特征值为（0.0490833989， 1.28402771），对应的特征向量分别为：(0.735178656,0.677873399)𝑇(−0.677873399,−0.735178656)𝑇(0.735178656,0.677873399)T(−0.677873399,−0.735178656)T,由于最大的k=1个特征值为1.28402771，对于的k=1个特征向量为(−0.677873399,−0.735178656)𝑇(−0.677873399,−0.735178656)T. 则我们的W=(−0.677873399,−0.735178656)𝑇(−0.677873399,−0.735178656)T

我们对所有的数据集进行投影𝑧(𝑖)=𝑊𝑇𝑥(𝑖)z(i)=WTx(i)，得到PCA降维后的10个一维数据集为：(-0.827970186， 1.77758033， -0.992197494， -0.274210416， -1.67580142， -0.912949103， 0.0991094375， 1.14457216, 0.438046137， 1.22382056)

核主成分分析KPCA介绍

在上面的PCA算法中，我们假设存在一个线性的超平面，可以让我们对数据进行投影。但是有些时候，数据不是线性的，不能直接进行PCA降维。这里就需要用到和支持向量机一样的核函数的思想，先把数据集从n维映射到线性可分的高维N>n,然后再从N维降维到一个低维度n', 这里的维度之间满足n'<n<N。

使用了核函数的主成分分析一般称之为核主成分分析(Kernelized PCA, 以下简称KPCA。假设高维空间的数据是由n维空间的数据通过映射𝜙产生。

则对于n维空间的特征分解：

\[ \sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}W=\lambda W \]

映射为

\[ \sum\limits_{i=1}^{m}\phi(x^{(i)})\phi(x^{(i)})^TW=\lambda W \]

通过在高维空间进行协方差矩阵的特征值分解，然后用和PCA一样的方法进行降维。一般来说，映射𝜙不用显式的计算，而是在需要计算的时候通过核函数完成。由于KPCA需要核函数的运算，因此它的计算量要比PCA大很多。

PCA算法总结

这里对PCA算法做一个总结。作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点，出现了很多PCA的变种，比如第六节的为解决非线性降维的KPCA，还有解决内存限制的增量PCA方法Incremental PCA，以及解决稀疏数据降维的PCA方法Sparse PCA等。

PCA算法的主要优点有：

1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。

2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。

3）计算方法简单，主要运算是特征值分解，易于实现。

PCA算法的主要缺点有：

1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

线性判别分析LDA原理总结

在主成分分析（PCA）原理总结中，我们对降维算法PCA做了总结。这里我们就对另外一种经典的降维方法线性判别分析（Linear Discriminant Analysis, 以下简称LDA）做一个总结。LDA在模式识别领域（比如人脸识别，舰艇识别等图形图像识别领域）中有非常广泛的应用，因此我们有必要了解下它的算法原理。

在学习LDA之前，有必要将其自然语言处理领域的LDA区别开来，在自然语言处理领域， LDA是隐含狄利克雷分布（Latent Dirichlet Allocation，简称LDA），他是一种处理文档的主题模型。我们本文只讨论线性判别分析，因此后面所有的LDA均指线性判别分析。

LDA的思想

LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。什么意思呢？我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。

可能还是有点抽象，我们先看看最简单的情况。假设我们有两类数据分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

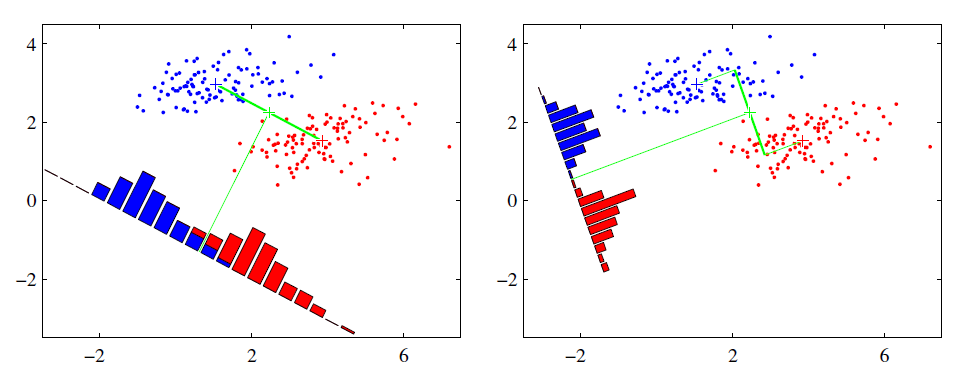
上图中国提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好，因为右图的黑色数据和蓝色数据各个较为集中，且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了，当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。

在我们将上面直观的内容转化为可以度量的问题之前，我们先了解些必要的数学基础知识，这些在后面讲解具体LDA原理时会用到。

瑞利商（Rayleigh quotient）与广义瑞利商（genralized Rayleigh quotient）

我们首先来看看瑞利商的定义。瑞利商是指这样的函数\(R(A,x)\):

\[ R(A,x) = \frac{x^HAx}{x^Hx} \]

其中\(𝑥\)为非零向量，而\(𝐴\)为\(𝑛×𝑛\)的Hermitan矩阵。所谓的Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵，即\(𝐴^𝐻=𝐴\)。如果我们的矩阵A是实矩阵，则满足\(𝐴^𝑇=𝐴\)的矩阵即为Hermitan矩阵。

瑞利商\(𝑅(𝐴,𝑥)\)有一个非常重要的性质，即它的最大值等于矩阵\(𝐴\)最大的特征值，而最小值等于矩阵\(𝐴\)的最小的特征值，也就是满足

\[ \lambda_{min} \leq \frac{x^HAx}{x^Hx} \leq \lambda_{max} \]

具体的证明这里就不给出了。当向量\(𝑥\)是标准正交基时，即满足\(𝑥^𝐻𝑥=1\)时，瑞利商退化为：\(𝑅(𝐴,𝑥)=𝑥^𝐻𝐴𝑥\)，这个形式在谱聚类和PCA中都有出现。

以上就是瑞利商的内容，现在我们再看看广义瑞利商。广义瑞利商是指这样的函数\(𝑅(𝐴,𝐵,𝑥)\):

\[ R(A,B,x) = \frac{x^HAx}{x^HBx} \]

其中𝑥为非零向量，而𝐴,𝐵为\(𝑛×𝑛\) 的Hermitan矩阵。𝐵为正定矩阵。它的最大值和最小值是什么呢？其实我们只要通过将其通过标准化就可以转化为瑞利商的格式。我们令\(𝑥=𝐵^{−1/2}𝑥^′\), 则分母转化为：

\[ x^HBx = x'^H(B^{-1/2})^HBB^{-1/2}x' = x'^HB^{-1/2}BB^{-1/2}x' = x'^Hx' \]

而分子转化为：