Path Aggregation Blcok

Apr 25, 2024
2 views
Computer Vision
# Object Detection # CV

FPN

1.结构区别

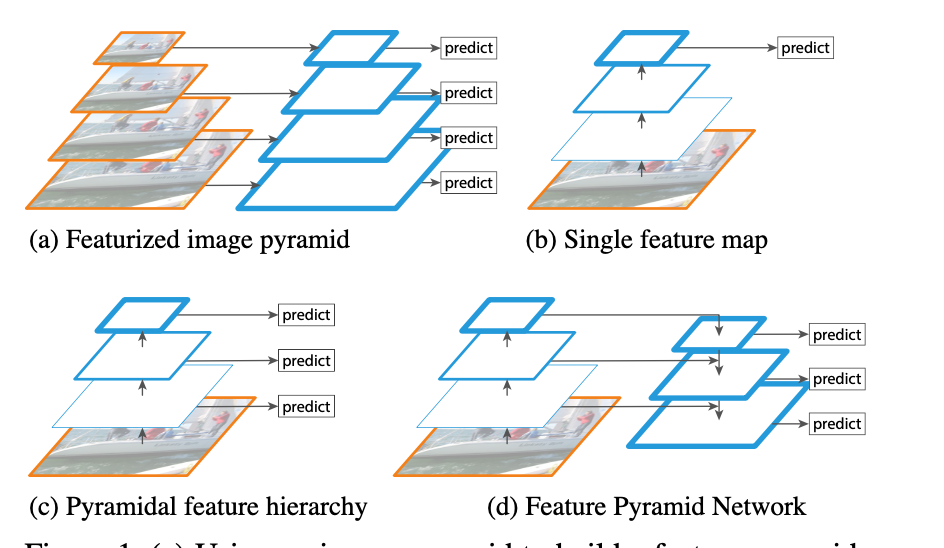
image

（a）图片金字塔生成特征金字塔：缩放图片比例

（b）通常的CNN网络结构

（c）多尺度特征融合的方式：像SSD（Single Shot Detector）就是采用这种多尺度特征融合的方式，没有上采样过程，即从网络不同层抽取不同尺度的特征做预测，这种方式不会增加额外的计算量。作者认为SSD算法中没有用到足够低层的特征（在SSD中，最低层的特征是VGG网络的conv4_3），而在作者看来足够低层的特征对于检测小物体是很有帮助的。

（d）FPN：这是本文要讲的网络，FPN主要解决的是物体检测中的多尺度问题，通过简单的网络连接改变，在基本不增加原有模型计算量的情况下，大幅度提升了小物体检测的性能。通过高层特征进行上采样和低层特征进行自顶向下的连接，而且每一层都会进行预测。

2.详细结构

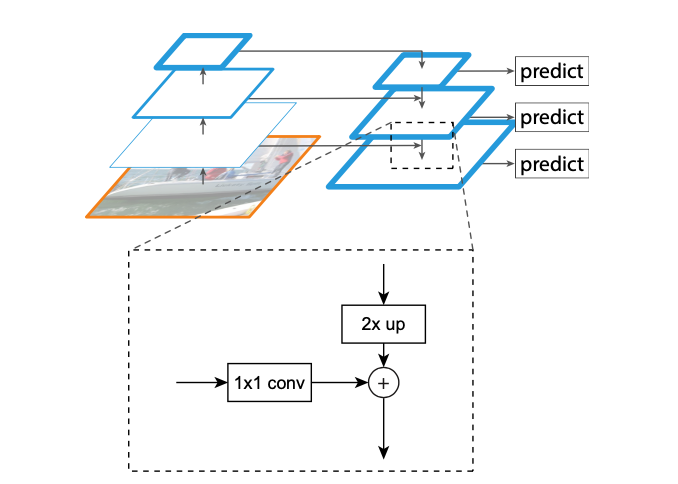
image

算法大致结构如下：一个自底向上的线路，一个自顶向下的线路，横向连接（lateral connection）。图中放大的区域就是横向连接，这里1*1的卷积核的主要作用是减少卷积核的个数，也就是减少了feature map的个数，并不改变feature map的尺寸大小。

  1. 自底向上：
  2. 自上而下：
  3. 横向连接：

PAN

PAN来自论文：Path Aggregation Network for Instance Segmentation。https://arxiv.org/abs/1803.01534

其结构如下所示：

image

FPN加入top-down的旁路连接，能给feature增加high-level语义,有利于分类。但是PAN论文作者觉得low-level的feature很有利于定位，虽然FPN中P5也间接融合了low-level的特征，但是信息流动路线太长了如红色虚线所示，其中会经过超多conv操作，本文在FPN的P2-P5又加了low-level的特征，最底层的特征流动到N2-N5只需要经过很少的层如绿色需要所示，主要目的是加速信息融合,缩短底层特征和高层特征之间的信息路径。down-top的融合做法是：

image

ASFF

ASFF来自论文：Learning Spatial Fusion for Single-Shot Object Detection

https://arxiv.org/pdf/1911.09516.pdf

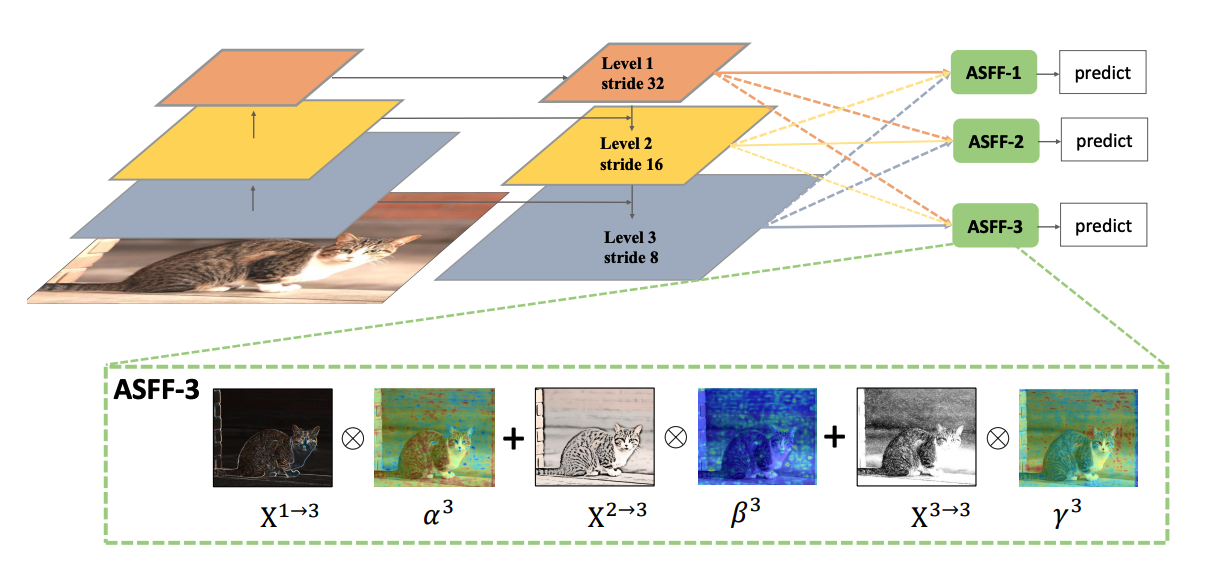
image

FPN操作是一个非常常用的用于对付大小尺寸物体检测的办法，作者指出FPN的缺点是不同尺度之间存在语义gap，举例来说基于iou准则，某个gt bbox只会分配到某一个特定层，而其余层级对应区域会认为是背景(但是其余层学习出来的语义特征其实也是连续相似的，并不是完全不能用的)，如果图像中包含大小对象，则不同级别的特征之间的冲突往往会占据要素金字塔的主要部分，这种不一致会干扰训练期间的梯度计算，并降低特征金字塔的有效性。一句话就是：目前这种concat或者add的融合方式不够科学。本文觉得应该自适应融合，自动找出最合适的融合特征, 简要思想就是：原来的FPN add方式现在变成了add基础上多了一个可学习系数，该参数是自动学习的，可以实现自适应融合效果，类似于全连接参数。

class ASFF(nn.Module): 
     def __init__(self, level, rfb=False, vis=False): 
        super(ASFF, self).__init__() 
        self.level = level 
        self.dim = [512, 256, 256] 
        self.inter_dim = self.dim[self.level] 
        # 每个level融合前，需要先调整到一样的尺度
        if level==0: 
            self.stride_level_1 = add_conv(256, self.inter_dim, 3, 2) 
            self.stride_level_2 = add_conv(256, self.inter_dim, 3, 2) 
            self.expand = add_conv(self.inter_dim, 1024, 3, 1) 
        elif level==1: 
            self.compress_level_0 = add_conv(512, self.inter_dim, 1, 1) 
            self.stride_level_2 = add_conv(256, self.inter_dim, 3, 2) 
           self.expand = add_conv(self.inter_dim, 512, 3, 1) 
       elif level==2: 
           self.compress_level_0 = add_conv(512, self.inter_dim, 1, 1) 
           self.expand = add_conv(self.inter_dim, 256, 3, 1) 
       compress_c = 8 if rfb else 16  #when adding rfb, we use half number of channels to save memory 

       self.weight_level_0 = add_conv(self.inter_dim, compress_c, 1, 1) 
       self.weight_level_1 = add_conv(self.inter_dim, compress_c, 1, 1) 
       self.weight_level_2 = add_conv(self.inter_dim, compress_c, 1, 1) 

       self.weight_levels = nn.Conv2d(compress_c*3, 3, kernel_size=1, stride=1, padding=0) 
       self.vis= vis 

    def forward(self, x_level_0, x_level_1, x_level_2): 
        if self.level==0: 
           level_0_resized = x_level_0 
           level_1_resized = self.stride_level_1(x_level_1) 

           level_2_downsampled_inter =F.max_pool2d(x_level_2, 3, stride=2, padding=1) 
           level_2_resized = self.stride_level_2(level_2_downsampled_inter) 

       elif self.level==1: 
           level_0_compressed = self.compress_level_0(x_level_0) 
           level_0_resized =F.interpolate(level_0_compressed, scale_factor=2, mode='nearest') 
           level_1_resized =x_level_1 
           level_2_resized =self.stride_level_2(x_level_2) 
       elif self.level==2: 
           level_0_compressed = self.compress_level_0(x_level_0) 
           level_0_resized =F.interpolate(level_0_compressed, scale_factor=4, mode='nearest') 
           level_1_resized =F.interpolate(x_level_1, scale_factor=2, mode='nearest') 
          level_2_resized =x_level_2 

       level_0_weight_v = self.weight_level_0(level_0_resized) 
       level_1_weight_v = self.weight_level_1(level_1_resized) 
       level_2_weight_v = self.weight_level_2(level_2_resized) 
       levels_weight_v = torch.cat((level_0_weight_v, level_1_weight_v, level_2_weight_v),1) 
       # 学习的3个尺度权重
       levels_weight = self.weight_levels(levels_weight_v) 
       levels_weight = F.softmax(levels_weight, dim=1) 
       # 自适应权重融合
       fused_out_reduced = level_0_resized * levels_weight[:,0:1,:,:]+\ 
                           level_1_resized * levels_weight[:,1:2,:,:]+\ 
                           level_2_resized * levels_weight[:,2:,:,:] 

       out = self.expand(fused_out_reduced) 

       if self.vis: 
           return out, levels_weight, fused_out_reduced.sum(dim=1) 
       else: 
          return out

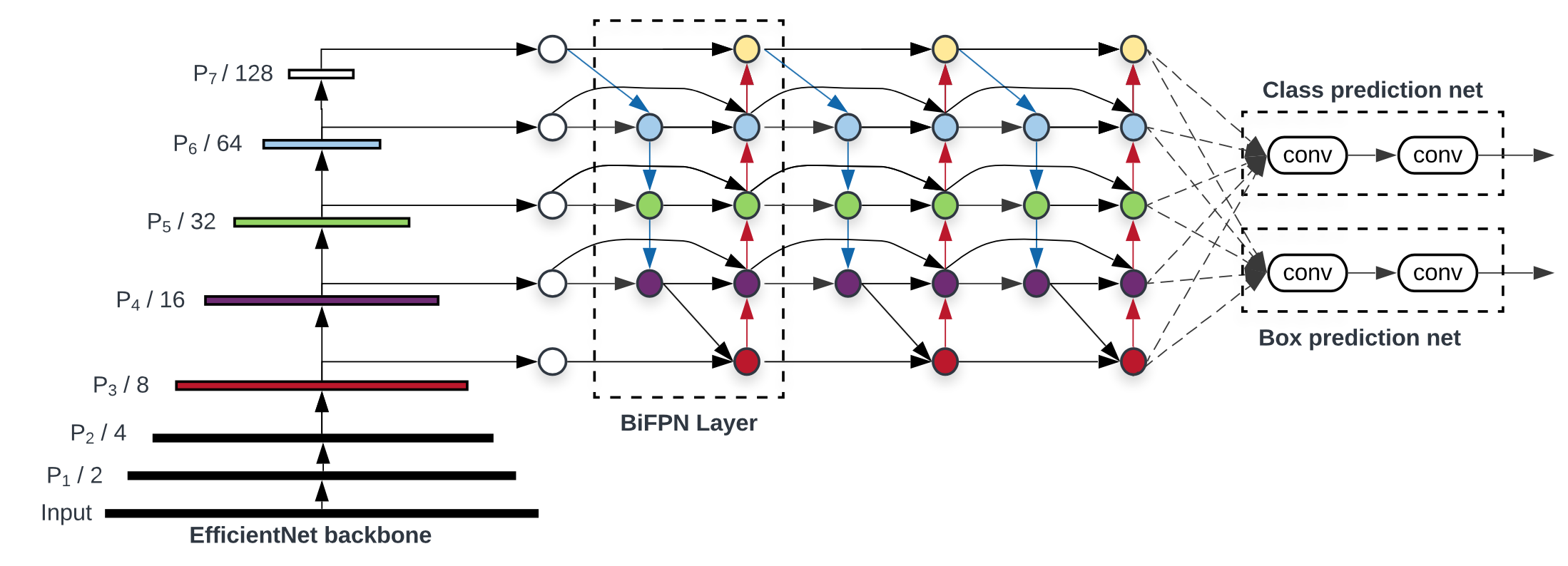
BiFPN（EfficientDet）

image

根据研究表明, PANET实际上在准确性上强于NAS-NET, 因此在应用领域, 更多人使用PANET, 但是PANET也有个问题, 它的计算成本也有点高, 为了实现优化的交叉链接, Efficient的作者对原始的PANET做了修改(图e/f).

作者在研究中发现:

  1. 如果一个节点只有一个输入边并且没有特征融合, 那么它对特征网络的融合贡献较小, 这个节点可以删除(Simplified PANET)
  2. 如果原始输入与输出节点处于同一级别, 则在它们之间添加一条额外的连接路径, 以便在不增加成本的情况下融合更多功能(BiFPN). 这点其实跟skip connection很相似.
  3. 将每个双向（自上而下＆自下而上）路径作为一个特征网络层, 并且重复叠加相同的特征网络层多次, 以实现更高层次的特征融合(BiFPN Layers). 具体重复几次是速度和精度之间的权衡, 因此会在下面的复合缩放部分介绍.
    上图最右侧便是最终优化过后的特征网络BiFPN.

Weighted BiFPN

多尺度特征融合旨在聚合不同分辨率的特征. 尽管我们获得了优化的特征网络, 但是我们同样面临一个和之前的FPN, PANET一样的困境, 那就是特征融合阶段所有的节点输入权重都是均等的, 我们做的仅仅是简单的相加. 但实际上, 由于不同特征的分辨率不同, 这些特征对最终融合后输出特征的贡献通常是不相等的, 我们需要对不同特征节点的输入有所偏重, 然而手动分配权重繁琐且无法泛化, 因此我们可以用神经网络去训练权重的分配, 让网络自己学习最佳值.

EfficientDet的作者分析了三种加权特征融合方式.

  1. Unbounded fusion:
    $$
    O_i=\sum_iw_i\cdot I_i
    $$

\(w_i\) 是可学习的权重, 可以是特征标量也可以是通道矢量, 亦或是像素的多维张量. 但是由于这些权重是无界的, 因此可能导致训练不稳定.

2. Softmax-based fusion:

\[ O_i = \sum_i\frac{e^{w_i}}{\sum_je^{w_j}}\cdot I_i \]

在分类网络中我们了解到, 如果希望权重值在0-1的有界范围内, 最好的办法之一就是通过Softmax将这些值转换为概率分布, 其中的概率值代表权重的重要性. 但是Softmax的计算成本是高昂的, 那有没有更好的方式呢?

3.Fast normalized fusion:

\[ O_i = \sum_i\frac{w_i}{\sum_j\epsilon + w_j}\cdot I_i \]

Relu是我们常用的激活函数, Relu的输出永远≥ 0, 再通过简单的正则化我们就可以将输出权重值控制在在0-1范围内. 这种方式相对前两种方式, 更加简单和高效, 因此EfficientDet中使用快速归一化融合特征网络.

EfficientDet结构

组合了backbone（使用了EfficientNet）和BiFPN（特征网络）和Box prediction net，整个框架就是EfficientDet的基本模型，结构如下图：

image