Kernel Logistic Regression
介绍如何将Kernel Trick引入到Logistic Regression,以及LR与SVM的结合
SVM与正则化
首先回顾Soft-Margin SVM的原始问题:
其中是训练数据违反边界的多少,没有违反的话,,反之,换句话说,目标函数的第二项就可以表示模型的损失。现在换一种方式来写,将二者结合起来: ,这一个等式就代表了上面的约束条件,这样上述问题,就与下面的无约束问题等价
这种形式与之前的L2 正则项很类似:
在L2中,通过最小化的同时控制的大小,防止模型过度复杂。从正则化的角度来看的话,Soft-Margin 的SVM其实就属于一种正则化模型,如下的对比:
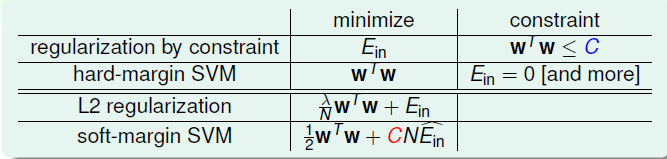
其中SVM中的与L2中的对应,越大,表示注重,那么就越小,正则化的效果相对就弱。
不过从正则化角度考虑Soft-Margin SVM的话,因为错误函数不是可微分的,因此不容易求解,因此我们采用的是二次规划来求解的。
SVM With Soft Binary Classification
上面我们定义了作为SVM的一种特殊的误差函数,也被叫做hinge error mesure,下面对比一下几种常见二分类的损失函数: PLA, Logistic Regression, Soft-Margin SVM,令:
然后把三者的图像绘出来,如下:
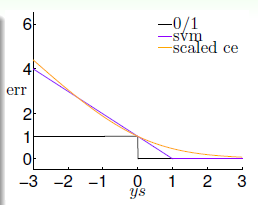
我们可以看出来SVM与LR的误差函数很类似,都表示0/1误差的上限,我们知道误差函数对于一个模型来说是至关重要的,那么从这个角度看的话,再结合第一部分Soft-Margin SVM与L2的正则项的形式很相似,那我们可以在一定程度上认为:Soft margin SVM L2 Regulared LR。 不过二者各有优点,比如SVM可以通过Kernel Trick 分类非线性的数据,而LR通过最大似然的方式则可以得到属于某类的概率值。
那我们可以将二者结合起来,也就是说使用SVM来做“软分类”,最终得到某类的概率值,有两种很直接的方式如下:
- 第一种: 首先使用SVM得到,然后直接使用sigmod函数计算概率,得到模型:
- 第二种: 使用SVM得到,然后作为LR的初始,再运行LR得到最终的模型
第一种方式最直接,也可以得到概率,但是没有用到LR的优点,比如最大似然。而第二种则没有用到Kernel Trick,充其量只是加快了LR的收敛速度。那么我们应该如何融合两者的优势呢?下面给出一个可能的模型,如下:
首先使用Kernel SVM得到, 对数据做变换,如果令, 那么后面就是一个很简单的LR模型:这样来看,第一个阶段其实就属于一种基于SVM的特征转换,或者说某种映射,将数据映射到了z-space,得到新的数据:。然后在新数据上跑一个LR模型,得到最终的结果,这里需要注意的是,得到的是一个一维的实数,这样大大减少了LR的计算复杂度。LR的两个参数的作用则是fine-tune(微调),平移或者放缩。一般情况下,如果SVM的效果好的话,。
这样一来,新的模型就可以结合了SVM与LR二者的优势,这种模型最早是由Platt提出的,因此也叫作Platt’s Model of Probabilistic SVM(概率模型),具体步骤总结如下:

如果把Kernel体现到模型的话,直接展开即可,最后的模型就是:
需要说明的是,这种模型是利用SVM的解,然后将其作为了LR的在Z-Space的近似解,实质上并没有真正的在Z-Space求解LR(A,B只是起到了微调作用),它的主要贡献是得到了概率SVM模型。
Kernel Logistic Regression(核逻辑回归)
这一部分则是介绍如何真正的在Z-Space使用Log-Reg模型,而非使用SVM的近似解,说到空间映射,Kernel Trick(核技巧)不得不提,那我们如何将Kernel运用到LR中呢?核到底是如何起作用的,回想SVM,我们从SVM的标准问题,转到对偶问题,然后因为对偶问题涉及到了Z-Space的内积,计算量很大,由此引出了Kernel Trick,,进而求出,实际上,只有将最优解表示为的线性组合,才能够利用核函数K,因为模型中需要计算:
试想如果最优解不是的线性组合,那模型中的就无法转为核函数的表达式了,那么核就无用武之地了(反过来想想,我们将数据从X-space转换到Z-Space的一个目的就是可以线性可分)。 因此,我们就可以得到一个结论,如果模型最优的是Z-Space的线性组合,那么我们就可以把Kernel Trick运用到该模型中。举几个前面的例子:
- SVM: ,其中是对偶问题中的拉格朗日乘子
- PLA: ,这里的则是在修正的过程中,这个点被分错误的次数
- LR: ,这里的可以理解为在用梯度下降法更新的步长
- …
上面的三种模型中的可以被数据表示,也就是说,我们都可以把Kernel Trick加到模型中(可以用来解决非线性可分),那到底有什么特征的模型,才满足条件呢?下面给出一个很重要的定理: Representer Theorem:
对于任意的正则化的线性模型,目标函数如下:
均有最优的参数
简单证明如下:
设最优解,其中
反证法,假设,将上述的分为两部分,先看第二部分的err,, 这部分与无关,看第一部分的正则项: ,矛盾产生,因为比有更小的误差。从而最优解与在同一个超平面,定理得证。
而前面介绍的L2正则化的Logistic Regression的目标函数:
很显然,LR的最优解: ,既然这样,那么我们就直接不再求,直接求解,然后加入Kernel Function,这样目标函数如下:
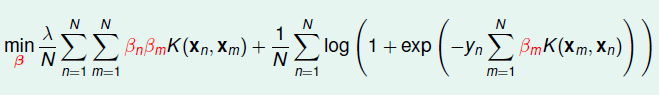
这是一个无约束的优化问题,可以使用梯度下降等方式来来得到最优解。
到此,我们成功将Kernel 加入到了Logistic Regression,得到的模型一般叫做Kernel Logistics Regression(KLR),这样就可以很好地解决非线性问题了。
最后说一句KLR其实相当于ββ的线性模型了,核函数KK 就相当于特征转换,左侧的写成矩阵形式就是: βTKβ相当于正则项。此外,在Kernel SVM中很稀疏,有很多项为0,Kernel LR中的则大部分都不为0。