池化： 池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。本质是 降采样，可以大幅减少网络的参数量。

常用的池化有：均值池化（mean pooling）、最大池化（max pooling）。

pooling操作没有参数量！！！

下面来说说这两种池化的区别与作用：

均值池化

主要用来抑制邻域值之间差别过大，造成的方差过大。
如，输入（2,10），通过均值池化后是（6），
对于输入的整体信息保存的很好，在计算机视觉中：因为一般前景的值大于背景，并且背景较多，所以对背景的保留效果好

反传

mean pooling的前向传播就是把一个patch中的值求取平均来做pooling，那么反向传播的过程也就是把某个元素的梯度等分为n份分配给前一层，这样就保证池化前后的梯度（残差）之和保持不变，还是比较理解的，图示如下

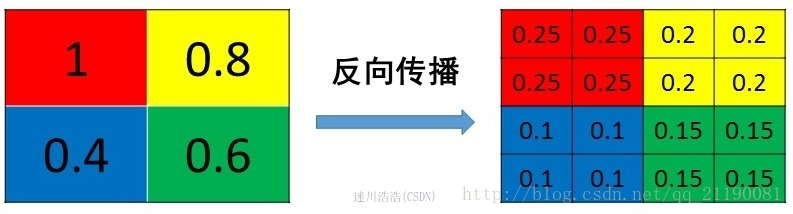
mean pooling比较容易让人理解错的地方就是会简单的认为直接把梯度复制N遍之后直接反向传播回去，但是这样会造成loss之和变为原来的N倍，网络是会产生梯度爆炸的。

最大池化

能够抑制网络参数误差造成的估计均值偏移的现象。
如，输入（1,5,3），最大池化后是（5），假如输入中的参数1，有误差，变为了1.5，这时输入是（1.5,5,3）,最大池化后结果还是（5）
在计算机视觉中：对纹理的提取较好！

反传

max pooling也要满足梯度之和不变的原则，max pooling的前向传播是把patch中最大的值传递给后一层，而其他像素的值直接被舍弃掉。那么反向传播也就是把梯度直接传给前一层某一个像素，而其他像素不接受梯度，也就是为0。所以max pooling操作和mean pooling操作不同点在于需要记录下池化操作时到底哪个像素的值是最大，也就是max id，这个可以看caffe源码的pooling_layer.cpp，下面是caffe框架max pooling部分的源码

// If max pooling, we will initialize the vector index part.
if (this->layer_param_.pooling_param().pool() == PoolingParameter_PoolMethod_MAX && top.size() == 1)
{
max_idx_.Reshape(bottom[0]->num(), channels_, pooled_height_,pooled_width_);
}

源码中有一个max_idx_的变量，这个变量就是记录最大值所在位置的，因为在反向传播中要用到，那么假设前向传播和反向传播的过程就如下图所示

性质

池化操作除了可以明显的减少参数量外，还能够保持对平移、伸缩、旋转等操作的不变性。

以平移不变性为例说明：
下图是输入维度是4×1，池化窗口3×1，步长为1，池化结果如下：

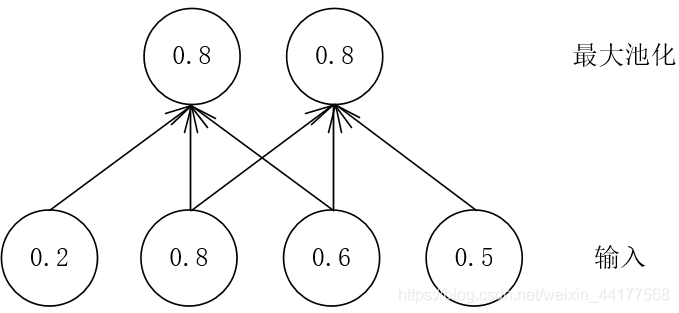
假如输入右移一位，发现最大池化后，结果是一致的。

当然上面只是举个例子，对于实际中的文本或图片数据，池化后肯定是有误差的，但是这点误差换来了参数量的大幅减少，训练速度大幅提升是划算的。