Reading

双指针

Jan 19, 2026
730 views
Algorithm
#Greedy

11. 盛最多水的容器

题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

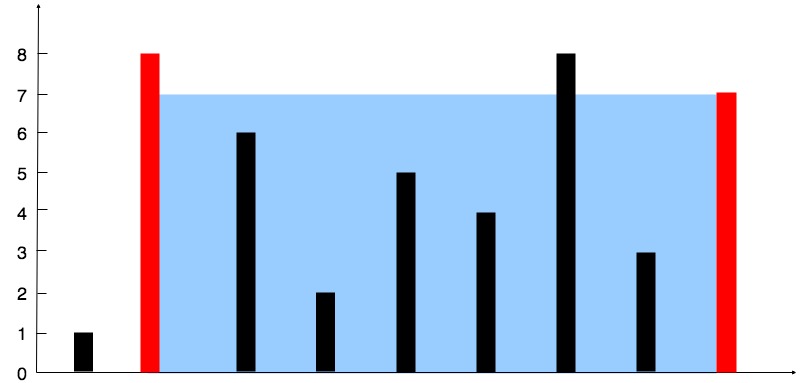
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1


提示：

  • n == height.length
  • 2 <= n <= 105
  • 0 <= height[i] <= 104

题解

在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 \(min(1,7)∗8=8\)。

此时我们需要移动一个指针。移动哪一个呢？直觉告诉我们，应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由两个指针指向的数字中较小值∗指针之间的距离决定的。如果我们移动数字较大的那个指针，那么前者「两个指针指向的数字中较小值」不会增加，后者「指针之间的距离」会减小，那么这个乘积会减小。因此，我们移动数字较大的那个指针是不合理的。因此，我们移动 数字较小的那个指针。

证明

在上面的分析部分，我们对这个问题有了一点初步的想法。这里我们定量地进行证明。

考虑第一步，假设当前左指针和右指针指向的数分别为 \(x\) 和 \(y\)，不失一般性，我们假设 \(x≤y\)。同时，两个指针之间的距离为 \(t\)。那么，它们组成的容器的容量为：

\[min(x,y)∗t=x∗t\]

我们可以断定，如果我们保持左指针的位置不变，那么无论右指针在哪里，这个容器的容量都不会超过 \(x∗t \)了。注意这里右指针只能向左移动，因为 我们考虑的是第一步，也就是 指针还指向数组的左右边界的时候。

我们任意向左移动右指针，指向的数为 \(y_1\)，两个指针之间的距离为 \(t_1\) ，那么显然有 \(t_1<t\)，并且 \(min(x,y_1 )≤min(x,y)\)：

  • 如果 \(y_1≤y\)，那么 \(min(x,y_1 )≤min(x,y)\)；
  • 如果 \(y_1>y\)，那么 \(min(x,y_1)=x=min(x,y)\)。

因此有：\(min(x,y_t)∗t_1<min(x,y)∗t\)

即无论我们怎么移动右指针，得到的容器的容量都小于移动前容器的容量。也就是说，这个左指针对应的数不会作为容器的边界了，那么我们就可以丢弃这个位置，将左指针向右移动一个位置，此时新的左指针于原先的右指针之间的左右位置，才可能会作为容器的边界。

这样以来，我们将问题的规模减小了 1，被我们丢弃的那个位置就相当于消失了。此时的左右指针，就指向了一个新的、规模减少了的问题的数组的左右边界，因此，我们可以继续像之前 考虑第一步 那样考虑这个问题：

求出当前双指针对应的容器的容量；

对应数字较小的那个指针以后不可能作为容器的边界了，将其丢弃，并移动对应的指针。

最后的答案是什么？

答案就是我们每次以双指针为左右边界（也就是「数组」的左右边界）计算出的容量中的最大值。

class Solution:
    def maxArea(self, height: List[int]) -> int:
        l, r = 0, len(height) - 1
        ans = 0
        while l < r:
            area = min(height[l], height[r]) * (r - l)
            ans = max(ans, area)
            if height[l] <= height[r]:
                l += 1
            else:
                r -= 1
        return ans

42. 接雨水

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

  • n == height.length
  • 1 <= n <= 2 * 104
  • 0 <= height[i] <= 105

题解

想象你在数组的任意一个位置 \(i\)，这个位置上方能积多少水？首先找到他左边最高的柱子leftmax，然后找到右边最高的柱子rightmax，则位置 \(i \)的积水量为min(leftmax, rightmax) - height[i]。
在双指针法中为什么leftmax<rightmax时就可以确定left处的积水量呢？这是因为此时left的左右屏障都以确定，且左边更短，储水量取决于leftmax，我们不需要知道left右边最高的高度是多少，只知道右边已经有一个比leftmax更高的屏障，确保水不会从右边流走，所以该位置的储水量就是leftmax-height[left]。

class Solution(object):
    def trap(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        n = len(height)
        left, right = 0, n-1
        left_max, right_max = 0, 0
        res = 0
        while left < right:
            left_max = max(left_max, height[left])
            right_max = max(right_max, height[right])
            if height[left] < height[ right]:
                res += min(right_max, left_max) - height[left]
                left += 1
            else:
                res += min(left_max, right_max) - height[right]
                right -= 1
        return res

240. 搜索二维矩阵 II

题目

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  • 每行的元素从左到右升序排列。
  • 每列的元素从上到下升序排列。


示例 1：

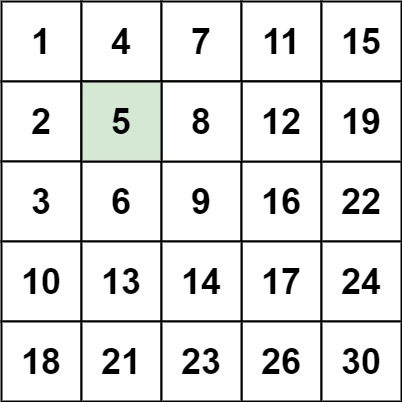
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

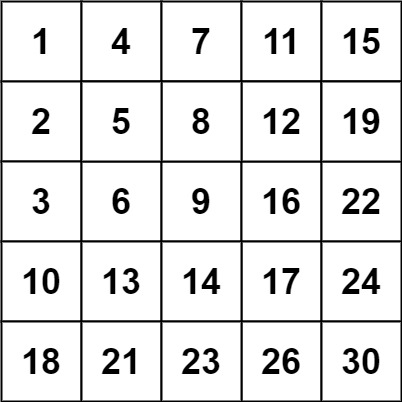
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false


提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= n, m <= 300
  • -109 <= matrix[i][j] <= 109
  • 每行的所有元素从左到右升序排列
  • 每列的所有元素从上到下升序排列
  • -109 <= target <= 109

题解

针对这种具有特定排序性质的矩阵，最优的解法是从矩阵的右上角（或左下角）开始搜索，类似于二叉搜索树（BST）的逻辑。

这种方法通常被称为“Z字形查找”或“鞍部点搜索”。

核心思路

我们可以将矩阵的右上角元素 \((0, n-1)\) 作为起始点。假设当前元素为 \(x\)，目标值为 \(\text{target}\)：

1. 如果 \(x = \text{target}\)：找到了目标值，返回 true。

2. 如果 \(x > \text{target}\)：

  • 由于列是升序排列的，位于 \(x\)下方的所有元素都必然大于 \(x\)，因此也必然大于 \(\text{target}\)。
  • 这意味着当前列不可能包含目标值。
  • 操作：向左移动一列（col--）。

3. 如果 \(x < \text{target}\)：

  • 由于行是升序排列的，位于 \(x\) 左侧的所有元素都必然小于 \(x\)，因此也必然小于 \(\text{target}\)。
  • 这意味着当前行不可能包含目标值。
  • 操作：向下移动一行（row++）。

重复上述步骤，直到找到目标值或超出矩阵边界。

def searchMatrix(matrix: list[list[int]], target: int) -> bool:
    # 处理边界情况
    if not matrix or not matrix[0]:
        return False
    
    m, n = len(matrix), len(matrix[0])
    
    # 从右上角开始 (row=0, col=n-1)
    row, col = 0, n - 1
    
    while row < m and col >= 0:
        current_val = matrix[row][col]
        
        if current_val == target:
            return True
        elif current_val > target:
            # 当前值比目标大，说明这一列剩下的数都比目标大，排除当前列，向左移
            col -= 1
        else:
            # 当前值比目标小，说明这一行左边的数都比目标小，排除当前行，向下移
            row += 1
            
    return False

复杂度分析

假设矩阵的大小为 \(m \times n\)。

  • 时间复杂度：\(O(m + n)\)
    • 在每一步迭代中，我们要么将行索引增加 \(1\)，要么将列索引减少 \(1\)。
    • 因此，我们最多会遍历 $$m$$ 行和 $$n$$ 列。
    • 总的搜索步数不会超过 \(m + n\)。这比对每一行进行二分查找的 \(O(m \log n)\) 要快（特别是当 \(m \approx n\) 时）。

* 空间复杂度：\(O(1)\)

    • 我们只需要常数级别的额外空间来存储 row和 col指针，不需要使用额外的递归栈或数据结构。

为什么不能从左上角开始？

如果从左上角 \((0, 0)\)开始，该元素是最小的。如果 \(\text{target}\)大于当前元素，我们既可以向右移动（变大），也可以向下移动（变大）。这就产生了歧义，无法像右上角那样通过一次比较就确定排除一行或一列，从而导致算法退化为回溯或更复杂的搜索。

如果 \(x < \text{target}\)，为什么不用 col++

简单来说：不用 col++（向右移），是因为我们能确定当前位置右边的元素一定比 target大

让我们通过逻辑推导来详细拆解一下：

  1. 为什么我们在当前列 col？

算法是从右上角开始的。如果我们现在的列指针在 col，说明我们是从 col + 1移动过来的（也就是之前执行过 col--）。

  1. 为什么之前会离开 col + 1列？

我们只有在遇到一个元素 大于target时，才会向左移动（col--）。

这意味着，在之前的某一行（设为 \(r'\)，其中 \(r' \le \text{current\_row}\)），我们一定在 col + 1列遇到过一个值 \(matrix[r'][col+1] > \text{target}\)。

  1. 列的升序性质决定了右边不可行

根据矩阵特性：每一列从上到下是升序的。

既然在之前的行 \(r'\)，col + 1列的值已经比 target大了，那么在当前行 current_row（因为它在 \(r'\)下方），col + 1列的值只会更大。

用数学语言描述：

\[matrix[\text{current\_row}][col+1] \ge matrix[r'][col+1] > \text{target}\]

### 结论

当 \(x < \text{target}\) 时：

1. 向左看（同一行左边）：因为行是升序，左边的数更小，肯定不是目标。

2. 向右看（同一行右边）：根据上面的推导，右边的数虽然比 \(x\) 大，但一定比 target 大，所以也不可能是目标。

3. 向下看（同一列下方）：这是唯一的希望，因为下方的数比 \(x\) 大，有可能等于 target。

所以，我们只能选择 row++。