INCOMING TRANSMISSION

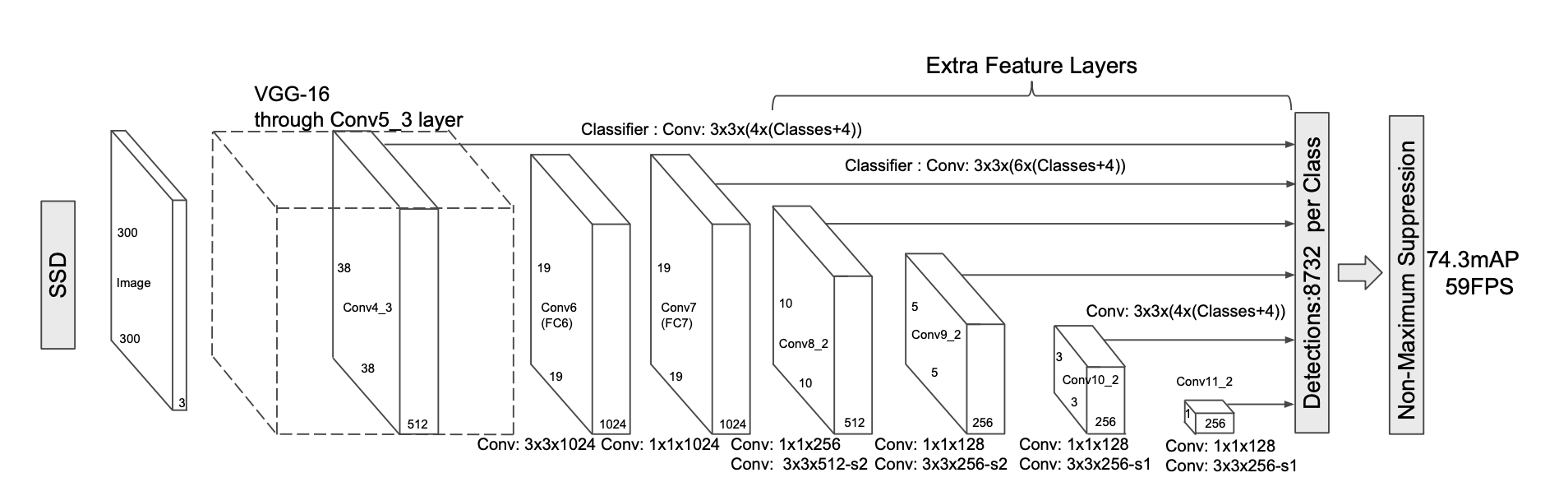
一、传统的图像金字塔 最开始在深度学习方法流行之前，对于不同尺度的目标，大家普遍使用将原图构建出不同分辨率的图像金字塔，再对每层金字塔用固定输入分辨率的分类器在该层滑动来检测目标，以求在金字塔底部检测出小目标；或者只用一个原图，在原图上，用不同分辨率的分类器来检测目标，以求在比较小的窗口分类器中检测到小目标。经典的基于简单矩形特征(Haar)+级联Adaboost与Hog特征+SVM的DPM目标识别框架，均使用图像金字塔的方式处理多尺度目标，早期的CNN目标识别框架同样采用该方式，但对图像金字塔中的每一层分别进行CNN提取特征，耗时与内存消耗均无法满足需求。但该方式毫无疑问仍然是最优的。值得一提的是，其实目前大多数深度学习算法提交结果进行排名的时候，大多使用多尺度测试。同时类似于SNIP使用...

SoftNMS/DIoUNMS softnms参考： SoftNMS 可以看到，SoftNMS与传统NMS的区别在于对score分数调整的处理。如果是传统的NMS操作，那么当 B 中的 b_i 和 [Math] 的IoU值大于阈值 N_t ，那么就从 B 和 S 中去除该box；对于SoftNMS而言是先计算 [Math] 与 b_i 的IoU，然后IoU经过一个函数输出最后与 s_i 相乘最终得到box的分数。 其中 s_i 的score遵循IoU越大，分数越低的原则（IoU越大，越可能是背景），所以 s_i 定义如下： 考虑到上式是不连续的，并且当达到N_t的NMS阈值时会施加突然的惩罚， 如果惩罚函数是连续的，那将是理想的，否则它可能导致检测结果的排序列表的突然改变（集合D中的scor...

SNIPER的关键是减少了SNIP的计算量。SNIP借鉴了multiscale training的思想进行训练，multiscale training是用图像金字塔作为模型的输入，这种做法虽然能够提高模型效果，但是计算量的增加也非常明显，因为模型需要处理每个scale图像的每个像素，而SNIPER（Scale Normalization for Image Pyramids with Efficient Resampling）算法以适当的比例处理ground truth（称为chips）周围的上下文区域，在训练期间每个图像生成的chips的数量会根据场景复杂度而自适应地变化，由于SNIPER在采样后的低分辨率的chips上运行，故其可以在训练期间收益于Batch Normalization，...

概述 众所周知，尽管基于Attention机制的Transformer类模型有着良好的并行性能，但它的空间和时间复杂度都是 [Math] 级别的， n 是序列长度，所以当 n 比较大时Transformer模型的计算量难以承受。近来，也有不少工作致力于降低Transformer模型的计算量，比如模型剪枝、量化、蒸馏等精简技术，又或者修改Attention结构，使得其复杂度能降低到 [Math] 甚至 [Math] 。 改变这一复杂度的思路主要有两种： 一是走稀疏化的思路，比如OpenAI的Sparse Attention，通过“只保留小区域内的数值、强制让大部分注意力为零”的方式，来减少Attention的计算量。经过特殊设计之后，Attention矩阵的大部分元素都是0，因此理论上它也能节...

总体流程 RPN RPN在Extractor输出的feature maps的基础之上，先增加了一个3x3卷积，然后利用两个1x1的卷积分别进行二分类（是否为正样本）和位置回归。进行分类的卷积核通道数为9×2（9个anchor，每个anchor二分类，使用交叉熵损失），进行回归的卷积核通道数为9×4（9个anchor，每个anchor有4个位置参数）。 接下来RPN做的事情就是利用（AnchorTargetCreator）将20000多个候选的anchor选出2000个proposal并采样256个positive 进行分类和回归位置loss计算。具体过程如下： proposal 前向过程中会做 NMS ： 1. 对所有 anchors 做前背景分类和bbox regression回归（lea...

前言 首先看论文题目。Swin Transformer： Hierarchical Vision Transformer using Shifted Windows。即：Swin Transformer是一个用了移动窗口的层级式Vision Transformer 所以Swin来自于 Shifted Windows ， 它能够使Vision Transformer像卷积神经网络一样，做层级式的特征提取，这样提取出来的特征具有多尺度的概念 ，这也是 Swin Transformer这篇论文的主要贡献。 标准的Transformer直接用到视觉领域有一些挑战，即： 多尺度问题：比如一张图片里的各种物体尺度不统一，NLP中没有这个问题； 分辨率太大：如果将图片的每一个像素值当作一个token直接输...

mAP定义及相关概念 mAP: mean Average Precision, 即各类别AP的平均值 AP: PR曲线下面积，后文会详细讲解 PR曲线: PrecisionRecall曲线 Precision: TP / (TP + FP) Recall: TP / (TP + FN) TP: IoU0.5的检测框数量（同一Ground Truth只计算一次） FP: IoU= 0, 0.1, 0.2, ..., 1共11个点时的Precision最大值，然后AP就是这11个Precision的平均值。 在VOC2010及以后，需要针对每一个不同的Recall值（包括0和1），选取其大于等于这些Recall值时的Precision最大值，然后计算PR曲线下面积作为AP值。 mAP计算示例 假...

NMS 过程： 1. 根据分类概率从小到大排序ABCDEF 1. 从最大概率F开始，F与A～E的IOU是否大于阈值 1. 大于的扔掉，从剩下的当中继续重复2～3 [代码] SoftNMS NMS算法保留score最高的预测框，并将与当前预测框重叠较多的proposals视作冗余，显然，在实际的检测任务中，这种思路有明显的缺点，比如对于稠密物体检测，当同类的两个目标距离较近时，如果使用原生的nms，就会导致其中一个目标不能被召回，为了提高这种情况下目标检测的召回率，SoftNMS应运而生。对于FasterRCNN在MSCOCO数据集上的结果，将NMS改成SoftNMS，mAP提升了1.1%。 它认为重叠较多的proposals也有可能包含有效目标，只不过重叠区域越大可能性越小。参见下图，NMS...

Preformer Performer的出发点还是标准的Attention，所以在它那里还是有 [Math] ，然后它希望将复杂度线性化，那就是需要找到新的 [Math] ，使得： [公式] 如果找到合理的从 [Math] 到 [Math] 的映射方案，便是该思路的最大难度了。 激活函数 线性Attention的常见形式如 式3，其中 [Math] 、 [Math] 是值域非负的激活函数。那么如何选取这个激活函数呢？Performer告诉我们，应该选择指数函数 [公式] 首先，我们来看它跟已有的结果有什么不一样。在 Transformers are RNNs 给出的选择是： [公式] 我们知道 1+x 正是 e^x 在 x=0 处的一阶泰勒展开，因此 [Math] 这个选择其实已经相当接近 ...

简介 承接 Transformers are RNNs 这篇论文 目的： 为了分析之前linear transformer的效果为什么不好。发现主要是两个原因造成的： 1. 无界梯度（unbounded gradient），会导致模型在训练时不稳定，收敛不好； 1. 注意力稀释（attention dilution），transformer在lower level时应该更关注局部特征，而higher level更关注全局特征，但线性transformer中的attention往往weight 更均匀化，不能聚焦在local区域上，因此称为attention稀释。 解决方案： 1. 对linear attention算出来的output接着做个normalization，形成NormForme...

01背包 描述 有N件物品和一个容量为V的背包。 第i件物品的体积是vi，价值是wi。 求解将哪些物品装入背包，可使这些物品的总体积不超过背包流量，且总价值最大。 二维动态规划 f[i][j] 表示只看前i个物品，总体积是j的情况下，总价值最大是多少。 result = max(f[n][0V]) f[i][j]: 不选第i个物品：f[i][j] = f[i1][j]; 选第i个物品：f[i][j] = f[i1][jv[i]] + w[i]（v[i]是第i个物品的体积） 两者之间取最大。 初始化：f[0][0] = 0 代码如下： [代码] 一维动态优化 从上面二维的情况来看，f[i] 只与f[i1]相关，因此只用使用一个一维数组[0v]来存储前一个状态。那么如何来实现呢？ 第一个问题：状...

起步 heapq 模块实现了适用于Python列表的最小堆排序算法。 堆是一个树状的数据结构，其中的子节点都与父母排序顺序关系。因为堆排序中的树是满二叉树，因此可以用列表来表示树的结构，使得元素 N 的子元素位于 2N + 1 和 2N + 2 的位置（对于从零开始的索引）。 本文内容将分为三个部分，第一个部分简单介绍 heapq 模块的使用；第二部分回顾堆排序算法；第三部分分析heapq中的实现。 heapq 的使用 创建堆有两个基本的方法：heappush() 和 heapify()，取出堆顶元素用 heappop()。 heappush() 是用来向已有的堆中添加元素，一般从空列表开始构建： [代码] 如果数据已经在列表中，则使用 heapify() 进行重排： [代码] 回顾堆排序算...