INCOMING TRANSMISSION

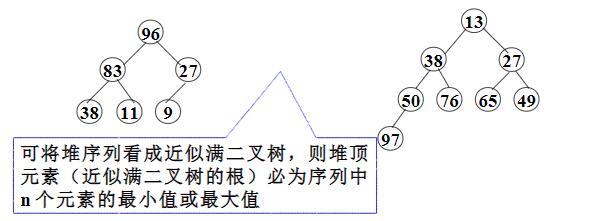
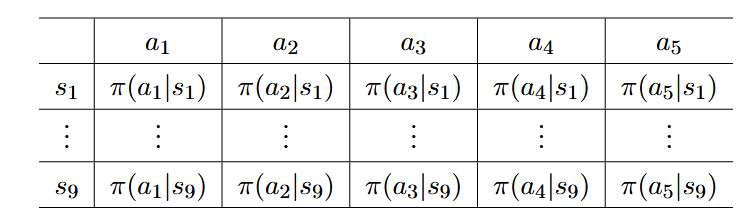
引言 时序差分（TemporalDifference，TD）方法是强化学习中的一类核心算法，它结合了动态规划与蒙特卡洛方法的优点。TD方法是无模型（modelfree）学习方法，不需要环境模型即可学习价值函数和最优策略。 TD方法的核心特点是通过比较不同时间步骤的估计值之间的差异来更新价值函数，这种差异被称为"时序差分误差"（TD error）。TD方法可以被视为解决贝尔曼方程或贝尔曼最优方程的特殊随机逼近算法。 基础TD算法：状态值函数学习 给定策略 [Math] ，基础TD算法用于估计状态值函数 [Math] 。假设我们有一些按照策略 [Math] 生成的经验样本 (s_0, r_1, s_1, ..., s_t, r_{t+1}, s_{t+1}, ...) ，TD算法的更新规则为： ...

引言 强化学习中，找到最优策略是核心目标。本文详细介绍三种能够找到最优策略的基础算法：价值迭代、策略迭代和截断策略迭代。这些算法属于动态规划范畴，需要系统模型，是后续无模型强化学习算法的重要基础。 在强化学习的发展路线中，这些算法处于"基础工具"到"算法/方法"的过渡阶段，是从"有模型"到"无模型"学习的重要桥梁。 价值迭代（Value iteration） 价值迭代算法基于收缩映射定理求解贝尔曼最优方程。其核心迭代公式为： [公式] 根据收缩映射定理，当 [Math] 时， v_k 和 [Math] 分别收敛到最优状态值和最优策略。 每次迭代包含两个步骤： 1. 策略更新步骤 （policy update step）：找到能解决以下优化问题的策略 1. 价值更新步骤（value updat...

Preformer Performer的出发点还是标准的Attention，所以在它那里还是有 [Math] ，然后它希望将复杂度线性化，那就是需要找到新的 [Math] ，使得： [公式] 如果找到合理的从 [Math] 到 [Math] 的映射方案，便是该思路的最大难度了。 激活函数 线性Attention的常见形式如 式3，其中 [Math] 、 [Math] 是值域非负的激活函数。那么如何选取这个激活函数呢？Performer告诉我们，应该选择指数函数 [公式] 首先，我们来看它跟已有的结果有什么不一样。在 Transformers are RNNs 给出的选择是： [公式] 我们知道 1+x 正是 e^x 在 x=0 处的一阶泰勒展开，因此 [Math] 这个选择其实已经相当接近 ...

01背包 描述 有N件物品和一个容量为V的背包。 第i件物品的体积是vi，价值是wi。 求解将哪些物品装入背包，可使这些物品的总体积不超过背包流量，且总价值最大。 二维动态规划 f[i][j] 表示只看前i个物品，总体积是j的情况下，总价值最大是多少。 result = max(f[n][0V]) f[i][j]: 不选第i个物品：f[i][j] = f[i1][j]; 选第i个物品：f[i][j] = f[i1][jv[i]] + w[i]（v[i]是第i个物品的体积） 两者之间取最大。 初始化：f[0][0] = 0 代码如下： [代码] 一维动态优化 从上面二维的情况来看，f[i] 只与f[i1]相关，因此只用使用一个一维数组[0v]来存储前一个状态。那么如何来实现呢？ 第一个问题：状...

起步 heapq 模块实现了适用于Python列表的最小堆排序算法。 堆是一个树状的数据结构，其中的子节点都与父母排序顺序关系。因为堆排序中的树是满二叉树，因此可以用列表来表示树的结构，使得元素 N 的子元素位于 2N + 1 和 2N + 2 的位置（对于从零开始的索引）。 本文内容将分为三个部分，第一个部分简单介绍 heapq 模块的使用；第二部分回顾堆排序算法；第三部分分析heapq中的实现。 heapq 的使用 创建堆有两个基本的方法：heappush() 和 heapify()，取出堆顶元素用 heappop()。 heappush() 是用来向已有的堆中添加元素，一般从空列表开始构建： [代码] 如果数据已经在列表中，则使用 heapify() 进行重排： [代码] 回顾堆排序算...

计数排序、基数排序、桶排序则属于非比较排序，算法时间复杂度O(n)，优于比较排序。但是也有弊端，会多占用一些空间，相当于是用空间换时间。 1. 计数排序： 计数排序的基本思想是：对每一个输入的元素a[i]，确定小于 a[i] 的元素个数。所以可以直接把 a[i] 放到它输出数组中的位置上。假设有5个数小于 a[i]，所以 a[i] 应该放在数组的第6个位置上。 实现代码如下： [代码] 2. 桶排序： 桶排序的基本思想是：把数组a划分为n个大小相同子区间（桶），每个子区间各自排序，最后合并。桶排序要求数据的分布必须均匀，不然可能会失效。计数排序是桶排序的一种特殊情况，可以把计数排序当成每个桶里只有一个元素的情况。 [代码] 算法实现步骤 1. 根据待排序集合中最大元素和最小元素的差值范围和映...

题目说明 在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。 示例 1: 输入: [3,2,1,5,6,4] 和 k = 2 输出: 5 示例 2: 输入: [3,2,3,1,2,4,5,5,6] 和 k = 4 输出: 4 题解 使用快排的思想 [代码]

Segment Anything Segment Anything（SA）项目：一个用于图像分割的新任务、新模型和新数据集 通过FM（基础模型）+prompt解决了CV中难度较大的分割任务，给计算机视觉实现基础模型+提示学习+指令学习提供了一种思路 关键：加大模型容量（构造海量的训练数据，或者构造合适的自监督任务来预训练） Segment Anything Task SAM的一部分灵感是来源于NLP中的基座模型(Foundation Model)，Foundation Model是OpenAI提出的一个概念，它指的是在超大量数据集上预训练过的大模型（如GPT系列、BERT），这些模型具有非常强大的 zeroshot 和 fewshot能力，结合prompt engineering和fine ...

引言与背景 策略梯度方法是强化学习中的一种重要方法，它标志着从基于价值的方法向基于策略的方法的重要转变。之前我们主要讨论了基于价值的方法（valuebased），而策略梯度方法则直接优化策略函数(policybased)，这是一个重要的进步。 当策略用函数表示时，策略梯度方法的核心思想是通过优化某些标量指标来获得最优策略。与传统的表格表示策略不同，策略梯度方法使用参数化函数 [Math] 来表示策略，其中 [Math] 是参数向量。这种表示方法也可以写成其他形式，如 [Math] 、 [Math] 或 [Math] 。 策略梯度方法具有多种优势： 更高效地处理大型状态/动作空间 具有更强的泛化能力 样本使用效率更高 策略表示：从表格到函数 当策略的表示从表格转变为函数时，存在以下几个关键区别...

💡 不断排除不存在解的区间，直至最后剩下一个 这里归纳最重要的部分： 分析题意，挖掘题目中隐含的 单调性； while (left < right) 退出循环的时候有 left == right 成立，因此无需考虑返回left还是right； 始终思考下一轮搜索区间是什么，如果是 [mid, right] 就对应 left = mid ，如果是 [left, mid 1] 就对应 right = mid 1，是保留 mid 还是 +1、−1 就在这样的思考中完成； 从一个元素什么时候不是解开始考虑下一轮搜索区间是什么 ，把区间分为 2个部分（一个部分肯定不存在目标元素，另一个部分有可能存在目标元素），问题会变得简单很多，这是一条 非常有用 的经验； 每一轮区间被划分成 2 部分，理解 区间划...

💡 GRPO相比PPO主要优势： 背景 GRPO是 DeepSeekMath model中提出的对PPO方法的改进策略： 强化学习(RL)在提升模型数学推理能力方面被证明是有效的 传统PPO算法需要较大训练资源 GRPO作为PPO的变体被提出,可以更高效地优化模型 PPO回顾 PPO的目标函数为: [公式] 其中: [Math] 和 [Math] 分别是当前和旧策略模型 A_t 是优势函数 [Math] 是裁剪相关的超参数 模型训练 如图1上所示，PPO需要同时训练一个Value Model [Math] 和策略模型， 同时需要reference model（通常从SFT model初始化）来限制策略模型训练保持和reference model的行为接近，而 Reward model用来计算...

kmp算法用于字符串的模式匹配，也就是找到模式字符串在目标字符串的第一次出现的位置比如abababc那么bab在其位置1处，bc在其位置5处，我们首先想到的最简单的办法就是蛮力的一个字符一个字符的匹配，但那样的时间复杂度会是O(mn)。kmp算法保证了时间复杂度为O(m+n)。 基本原理 举个例子： 发现x与c不同后，进行移动 a与x不同，再次移动 此时比较到了c与y， 于是下一步移动成了下面这样 这一次的移动与前两次的移动不同，之前每次比较到上面长字符串的字符位置后，直接把模式字符串的首字符与它对齐，这次并没有，原因是这次移动之前，y与c对齐，但是y前边的ab是与自己的前缀ab一样，于是ab并不用再比较，直接从第三个位置开始比较，如图： 所以说kmp算法对于这种情况就直接使用当前比较字符之...