INCOMING TRANSMISSION

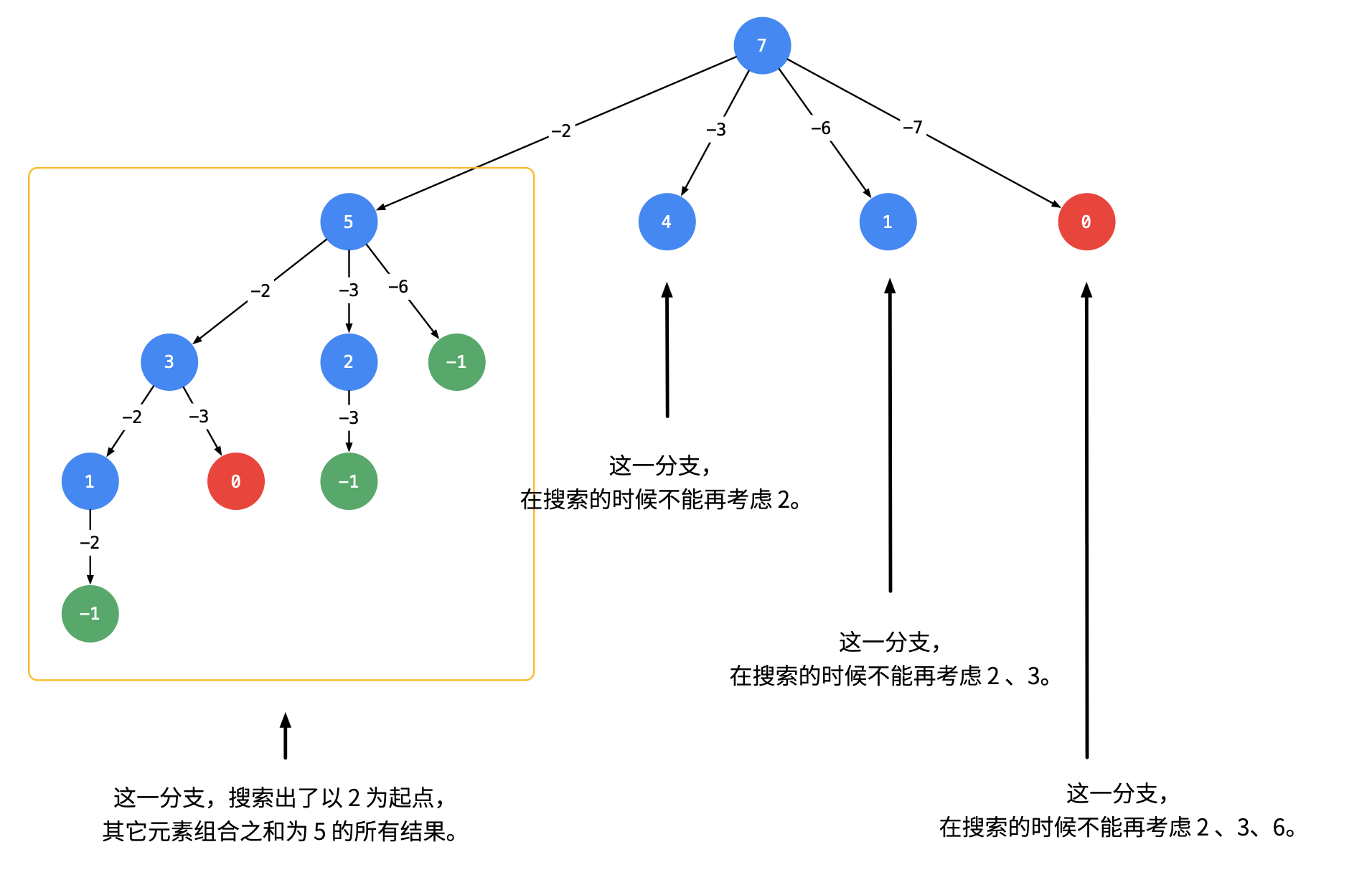
1. 可以重复选取 给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的数字可以无限制重复被选取。 画出树状搜索图如下， 为了去除重复的情况， 我们需要按照某种顺序搜索，具体做法是：每一次搜索的时候，设置下一轮搜索的起点 [代码] 2. 不能被重复选取 与上面的区别在于 1. index每次不要重复搜索，而是去寻找下一个 1. 排除重复的元素 [代码]

概述 问题定义 广义的 Gaze Estimation 泛指与眼球、眼动、视线等相关的研究，因此有不少做 saliency 和 egocentric 的论文也以 gaze 为关键词。而本文介绍的 Gaze Estimation 主要以眼睛图像或人脸图像为处理对象，估算人的视线方向或注视点位置， 如下图所示。 gaze角度的表示一般使用一个3d向量作为表示，也可以转换为pitch 和yaw角度，具体可参考 Model Gaze模型一般使用回归模型，所以这里基本只介绍一些在gaze model中使用的小技巧 Rle Loss 实际问题

01背包 描述 有N件物品和一个容量为V的背包。 第i件物品的体积是vi，价值是wi。 求解将哪些物品装入背包，可使这些物品的总体积不超过背包流量，且总价值最大。 二维动态规划 f[i][j] 表示只看前i个物品，总体积是j的情况下，总价值最大是多少。 result = max(f[n][0V]) f[i][j]: 不选第i个物品：f[i][j] = f[i1][j]; 选第i个物品：f[i][j] = f[i1][jv[i]] + w[i]（v[i]是第i个物品的体积） 两者之间取最大。 初始化：f[0][0] = 0 代码如下： [代码] 一维动态优化 从上面二维的情况来看，f[i] 只与f[i1]相关，因此只用使用一个一维数组[0v]来存储前一个状态。那么如何来实现呢？ 第一个问题：状...

起步 heapq 模块实现了适用于Python列表的最小堆排序算法。 堆是一个树状的数据结构，其中的子节点都与父母排序顺序关系。因为堆排序中的树是满二叉树，因此可以用列表来表示树的结构，使得元素 N 的子元素位于 2N + 1 和 2N + 2 的位置（对于从零开始的索引）。 本文内容将分为三个部分，第一个部分简单介绍 heapq 模块的使用；第二部分回顾堆排序算法；第三部分分析heapq中的实现。 heapq 的使用 创建堆有两个基本的方法：heappush() 和 heapify()，取出堆顶元素用 heappop()。 heappush() 是用来向已有的堆中添加元素，一般从空列表开始构建： [代码] 如果数据已经在列表中，则使用 heapify() 进行重排： [代码] 回顾堆排序算...

计数排序、基数排序、桶排序则属于非比较排序，算法时间复杂度O(n)，优于比较排序。但是也有弊端，会多占用一些空间，相当于是用空间换时间。 1. 计数排序： 计数排序的基本思想是：对每一个输入的元素a[i]，确定小于 a[i] 的元素个数。所以可以直接把 a[i] 放到它输出数组中的位置上。假设有5个数小于 a[i]，所以 a[i] 应该放在数组的第6个位置上。 实现代码如下： [代码] 2. 桶排序： 桶排序的基本思想是：把数组a划分为n个大小相同子区间（桶），每个子区间各自排序，最后合并。桶排序要求数据的分布必须均匀，不然可能会失效。计数排序是桶排序的一种特殊情况，可以把计数排序当成每个桶里只有一个元素的情况。 [代码] 算法实现步骤 1. 根据待排序集合中最大元素和最小元素的差值范围和映...

题目说明 在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。 示例 1: 输入: [3,2,1,5,6,4] 和 k = 2 输出: 5 示例 2: 输入: [3,2,3,1,2,4,5,5,6] 和 k = 4 输出: 4 题解 使用快排的思想 [代码]

💡 不断排除不存在解的区间，直至最后剩下一个 这里归纳最重要的部分： 分析题意，挖掘题目中隐含的 单调性； while (left < right) 退出循环的时候有 left == right 成立，因此无需考虑返回left还是right； 始终思考下一轮搜索区间是什么，如果是 [mid, right] 就对应 left = mid ，如果是 [left, mid 1] 就对应 right = mid 1，是保留 mid 还是 +1、−1 就在这样的思考中完成； 从一个元素什么时候不是解开始考虑下一轮搜索区间是什么 ，把区间分为 2个部分（一个部分肯定不存在目标元素，另一个部分有可能存在目标元素），问题会变得简单很多，这是一条 非常有用 的经验； 每一轮区间被划分成 2 部分，理解 区间划...

kmp算法用于字符串的模式匹配，也就是找到模式字符串在目标字符串的第一次出现的位置比如abababc那么bab在其位置1处，bc在其位置5处，我们首先想到的最简单的办法就是蛮力的一个字符一个字符的匹配，但那样的时间复杂度会是O(mn)。kmp算法保证了时间复杂度为O(m+n)。 基本原理 举个例子： 发现x与c不同后，进行移动 a与x不同，再次移动 此时比较到了c与y， 于是下一步移动成了下面这样 这一次的移动与前两次的移动不同，之前每次比较到上面长字符串的字符位置后，直接把模式字符串的首字符与它对齐，这次并没有，原因是这次移动之前，y与c对齐，但是y前边的ab是与自己的前缀ab一样，于是ab并不用再比较，直接从第三个位置开始比较，如图： 所以说kmp算法对于这种情况就直接使用当前比较字符之...

题意 给定平面上一个圆的圆心位置和半径，从圆中以均匀的概率随机选取点。 分析 拒绝取样 其实我的第一反应是用拒绝取样（Rejection Sampling）的思路来做：首先从这个圆的与坐标轴平行的外切正方形中均匀随机选取点，然后判断点是否位于圆中；如果不在，重新生成一个新的点，再次进行判断；否则直接返回。 直觉上来说，拒绝取样显然是正确的；不过我们可以用一种稍微更加形式化的方法来描述。（以下内容参考了拒绝采样（reject sampling）的简单认识，非常直观形象。） 下图是一个随机变量的密度函数曲线，试问如何获得这个随机变量的样本呢？ 如果你像我一样，已经把概率论与数理统计统统还给数学老师了，那么提示一下，概率密度函数（PDF）是累积分布函数（CDF）的导数，反映的是概率的“密集程度”。...

根据一棵树的先序遍历和中序遍历，或者后序遍历和中序遍历序列，都可以唯一地确定一棵树。 树中的节点，分为度为0，1，2的结点。如果树中只有一个节点，那么可以唯一确定一棵树，即只有一个节点的树。 当树中结点个数大于等于2的情况，树中的叶子结点和它的父亲结点中，至少有一种存在如下的情况。（为方便起见，我们先从叶子节点入手） case 1: case2: case 3: A D F / \ / \ B C E G 即，叶子结点的父亲有两个孩子，只有左孩子，只有右孩子的情况。我们只需要证明，如果树存在这三种结构中的哪一种，可以唯一确定一棵树，什么情况下又不能唯一确定一棵树呢? 1. case 1: A / \ B C 前序遍历： ABC， 后序遍历： BCA 现在，我们根据遍历序列，看看能否得到另一种...

近期，人脸识别研究领域的主要进展之一集中在了 Softmax Loss 的改进之上；本文从两种主要的改进方式——做归一化以及增加类间 margin——展开梳理，介绍了近年来基于 Softmax 的 Loss 的研究进展。 Softmax简介 Softmax Loss 因为其易于优化，收敛快等特性被广泛应用于图像分类领域。然而，直接使用 softmax loss 训练得到的 feature 拿到 retrieval，verification 等“需要设阈值”的任务时，往往并不够好。 这其中的原因还得从 Softmax 的本身的定义说起，Softmax loss 在形式上是 softmax 函数加上交叉熵损失，它的目的是让所有的类别在概率空间具有最大的对数似然，也就是保证所有的类别都能分类正确，...