INCOMING TRANSMISSION

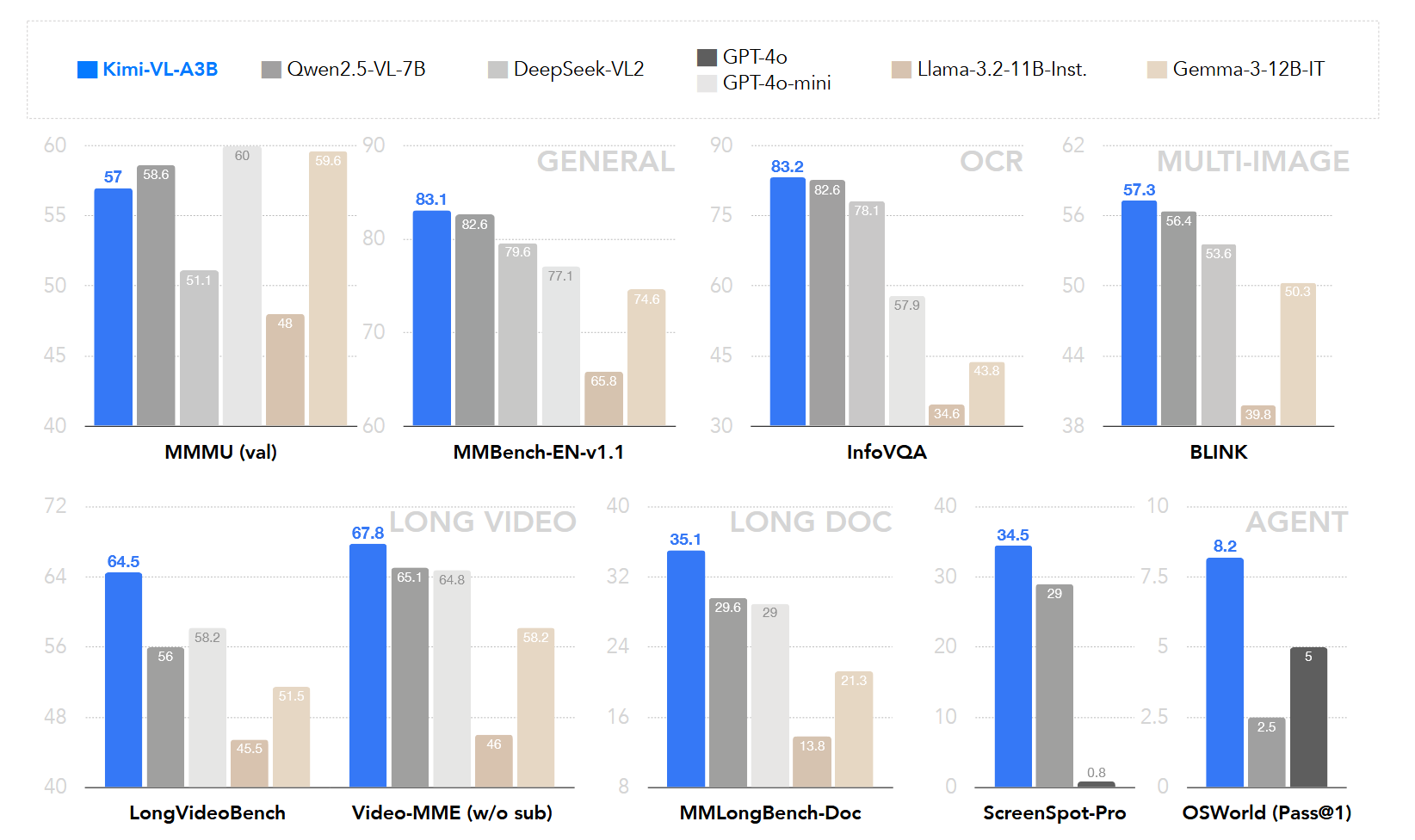
模型概述 KimiVL 是一个高效的开源混合专家视觉语言模型(VLM)，它提供先进的多模态推理、长上下文理解和强大的代理能力，同时在语言解码器中仅激活 2.8B 参数(KimiVLA3B)。该模型在多种挑战性任务中表现出色，包括一般用途的视觉语言理解、多轮代理任务、大学水平的图像和视频理解、OCR、数学推理和多图像理解等. 模型架构 KimiVL 的架构由三个主要部分组成： MoE语言模型 Moonlight MoE language model with only 2.8B activated (16B total) parameters 视觉模型 400M nativeresolution MoonViT vision encoder. MLP Projector MoonViT: 原生...

给定一个包含 n 维数据 x 的数据集 D , 简单起见，假设数据 [Math] . 由于真正对联合分布建模的时候， x，y 都是随机变量，故而只需讨论 p(X)=p(x_1,...,x_n) 即可，毕竟只需要令 x_n=y 即可。 给定一个具体的任务，如MNIST中的手写数字二值图分类，从Generative的角度进行Represent，并在Inference中Learning. 下面先介绍： 描述如何对这个MINST任务建模 p(X,Y) （Representation） 对MNIST任务建模 对于一张pixel为 [Math] 大小的图片，令 x_1 表示第一个pixel的随机变量， [Math] ，需明确： 任务目标：学习一个模型分布 [Math] ，使采样时 [Math] ， x ...

AdamW目前是大语言模型训练的默认优化器，而大部分资料对Adam跟AdamW区别的介绍都不是很明确，在此梳理一下Adam与AdamW的计算流程，明确一下二者的区别。 TLDR：AdamW将优化过程中使用的针对网络权重的衰减项（或者叫正则项）从loss中单独拿了出来，不参与Adam中一二阶动量的计算。 下面是二者的详细对比： Adam 首先是Adam，给定在迭代步数 t 时模型的参数 [Math] 与梯度 g_t ，Adam的计算公式如下： [公式] 式(1)用于计算梯度的一阶指数滑动平均 式(2)用于计算梯度的二阶项的指数滑动平均 式(3)与(4)对计算得到的指数滑动平均值进行消偏 式(5)为Adam的更新公式，其可以拆成两部分理解：动量更新与自适应学习率。 AdamW AdamW 相对与...

引言 DDPG同样使用了ActorCritic的结构，Deterministic的确定性策略是和随机策略相对而言的，对于某一些动作集合来说，它可能是连续值，或者非常高维的离散值，这样动作的空间维度极大。如果我们使用随机策略，即像DQN一样研究它所有的可能动作的概率，并计算各个可能的动作的价值的话，那需要的样本量是非常大才可行的。于是有人就想出使用确定性策略来简化这个问题。 作为随机策略，在相同的策略，在同一个状态 s 处，采用的动作 [Math] 是基于一个概率分布的，即是不确定的。而确定性策略则决定简单点，虽然在同一个状态处，采用的动作概率不同，但是最大概率只有一个，如果我们只取最大概率的动作，去掉这个概率分布，那么就简单多了。即作为确定性策略，相同的策略，在同一个状态处，动作是唯一确定的...

引言与背景 价值函数方法是强化学习中的核心技术，它解决了传统表格方法在处理大型状态或动作空间时的效率问题。本文探讨了从表格表示向函数表示的转变，这是强化学习算法发展的重要里程碑。 在强化学习的发展路径中，价值函数方法位于从基于模型到无模型、从表格表示到函数表示的演进过程中。它结合了时序差分学习的思想，并通过函数近似技术来处理复杂环境。 价值表示：从表格到函数 表格与函数表示的对比 传统的表格方法将状态值存储在一个表格中： 而函数近似方法则使用参数化函数来表示这些值，例如： [公式] 其中 [Math] 称作是状态 s 的特征向量， w 是参数向量。 两种不同的表现形式的区别主要体现在以下几个方面： 值的检索方式 值的更新方式 函数复杂度与近似能力 函数的复杂度决定了其近似的能力： 一阶线性函...

最优策略（Optimal Policy ） 之前在 贝尔曼方程中说过，状态值可以用来评估一个策略是好是坏，这里给出正式的概念： [公式] 那么此时 [Math] 比 [Math] ”更好“ 最优状态值（Optimal State Value）： 最优策略（Optimal Policy）： 性质： 为了说明上述性质， 我们研究贝尔曼最优方程 Bellman optimality equation（BOE） 贝尔曼最优方程（BOE） 定义 分析最优策略和最优状态值的工具是贝尔曼最优方程（BOE）。通过求解此方程，我们可以获得最优策略和最优状态值。 对于每个 s∈S ，BOE 的elementwise表达式为: [公式] 其中， v(s) 和 [Math] 是待求解的未知变量， π(s) 表示状态...

概述与理论背景 ActorCritic方法是强化学习中的一类重要算法，它巧妙地结合了基于策略(policybased)和基于价值(valuebased)的方法。在这种结构中，"Actor"指策略更新步骤，负责根据策略执行动作；而"Critic"指价值更新步骤，负责评估Actor的表现。从另一个角度看，ActorCritic方法本质上仍是策略梯度算法，可以通过扩展策略梯度算法获得。 ActorCritic方法在强化学习中的位置非常重要，它既保留了策略梯度方法直接优化策略的优势，又利用了值函数方法的效率。这种结合使得ActorCritic方法成为解决复杂强化学习问题的强大工具。 最简单的ActorCritic算法(QAC) QAC算法通过扩展策略梯度方法得到。策略梯度方法的核心思想是通过最大化标...

状态价值（State values） 定义 状态价值是强化学习中的核心概念，用于衡量Agent从某个状态出发、遵循特定策略后所能获得的期望回报。 数学表达为： [公式] 其中： [Math] ：状态 s 的状态价值函数（statevalue function） 或者简称为 状态价值（state value）； [Math] ：智能体遵循的策略； [Math] ：从当前时间步 t 开始的折扣回报； [Math] ：折扣因子，用于平衡即时奖励和未来奖励。 状态价值的特点 依赖于状态 s ：状态价值是条件期望，条件是智能体从状态 s 开始。 依赖于策略 [Math] ：不同策略会生成不同的轨迹，从而影响状态价值。 与时间步无关：状态价值是一个固定值，与当前时间步 t 无关。 代表一个状态的价值。如...

概述 Kimi k1.5采用了一种简化而有效的强化学习框架，其核心在于长上下文扩展和改进的策略优化方法，而不依赖于更复杂的技术如蒙特卡洛树搜索、价值函数和过程奖励模型。 问题设定 给定训练数据集 D = \{(x_i, y^_i)\}_{i=1}^n ，其中包含问题 x_i 和对应的真实答案 y^_i ，目标是训练一个策略模型 [Math] 来准确解决测试问题。在复杂推理场景中，思维链(CoT)方法提出使用一系列中间步骤 z = (z_1, z_2, ..., z_m) 来连接问题 x 和答案 y ，每个 z_i 是解决问题的重要中间步骤。 当解决问题 x 时，思维 [Math] 被自回归采样，最终答案 [Math] 。 强化学习目标 基于真实答案 y^ ，分配一个值 [Math] , Ki...

💡 引言 Trust Region Policy Optimization (TRPO) 是2015年的ICML会议上提出的一种强大的基于策略的强化学习算法。TRPO 解决了传统策略梯度方法中的一些关键问题，特别是训练不稳定和步长选择困难的问题。与传统策略梯度算法相比，TRPO 具有更高的稳健性和样本效率，能够在复杂环境中取得更好的性能。 优化基础 在深入了解 TRPO 之前，我们需要先简单回顾一些优化方法的基础知识。 梯度上升法 梯度上升法是一种迭代优化算法，用于寻找函数的局部最大值。 目标：找到使目标函数 [Math] 最大化的参数 [Math] ： [公式] 梯度上升迭代过程： 1. 在当前参数 [Math] 处计算梯度： [Math] 1. 更新参数： 梯度上升法的主要问题是学习率的...

mAP定义及相关概念 mAP: mean Average Precision, 即各类别AP的平均值 AP: PR曲线下面积，后文会详细讲解 PR曲线: PrecisionRecall曲线 Precision: TP / (TP + FP) Recall: TP / (TP + FN) TP: IoU0.5的检测框数量（同一Ground Truth只计算一次） FP: IoU= 0, 0.1, 0.2, ..., 1共11个点时的Precision最大值，然后AP就是这11个Precision的平均值。 在VOC2010及以后，需要针对每一个不同的Recall值（包括0和1），选取其大于等于这些Recall值时的Precision最大值，然后计算PR曲线下面积作为AP值。 mAP计算示例 假...

引言 时序差分（TemporalDifference，TD）方法是强化学习中的一类核心算法，它结合了动态规划与蒙特卡洛方法的优点。TD方法是无模型（modelfree）学习方法，不需要环境模型即可学习价值函数和最优策略。 TD方法的核心特点是通过比较不同时间步骤的估计值之间的差异来更新价值函数，这种差异被称为"时序差分误差"（TD error）。TD方法可以被视为解决贝尔曼方程或贝尔曼最优方程的特殊随机逼近算法。 基础TD算法：状态值函数学习 给定策略 [Math] ，基础TD算法用于估计状态值函数 [Math] 。假设我们有一些按照策略 [Math] 生成的经验样本 (s_0, r_1, s_1, ..., s_t, r_{t+1}, s_{t+1}, ...) ，TD算法的更新规则为： ...