计算几何(Computational Geometry),是一系列使用计算机解决几何问题的算法。与解析几何相比,计算几何更适合计算机运算,精度较高,运算速度较快,并且易于编写。 浮点误差 程序设计中,考虑到浮点数 double 有精度误差,在比较时,通常允许一定的误差,即对于两个数 a 、 b ,如果 [Math] ,则认为 a=b 。一般根据题目要求, d (代码中命名为 EPS)取一个较小值,如 10^{8} 。 [代码] 向量 向量(vector)是一个有大小和方向的量,在几何中,它被表示为带箭头的线段。向量可以用起点和终点的坐标来表示 —— 从点 A到点B 的向量表示为 [Math] 。 向量的书写,两个大写字母上加一个箭头(表示方向) [Math] 向量没有位置,即向量可以在平面内...
Computer Vision
2026-01-11
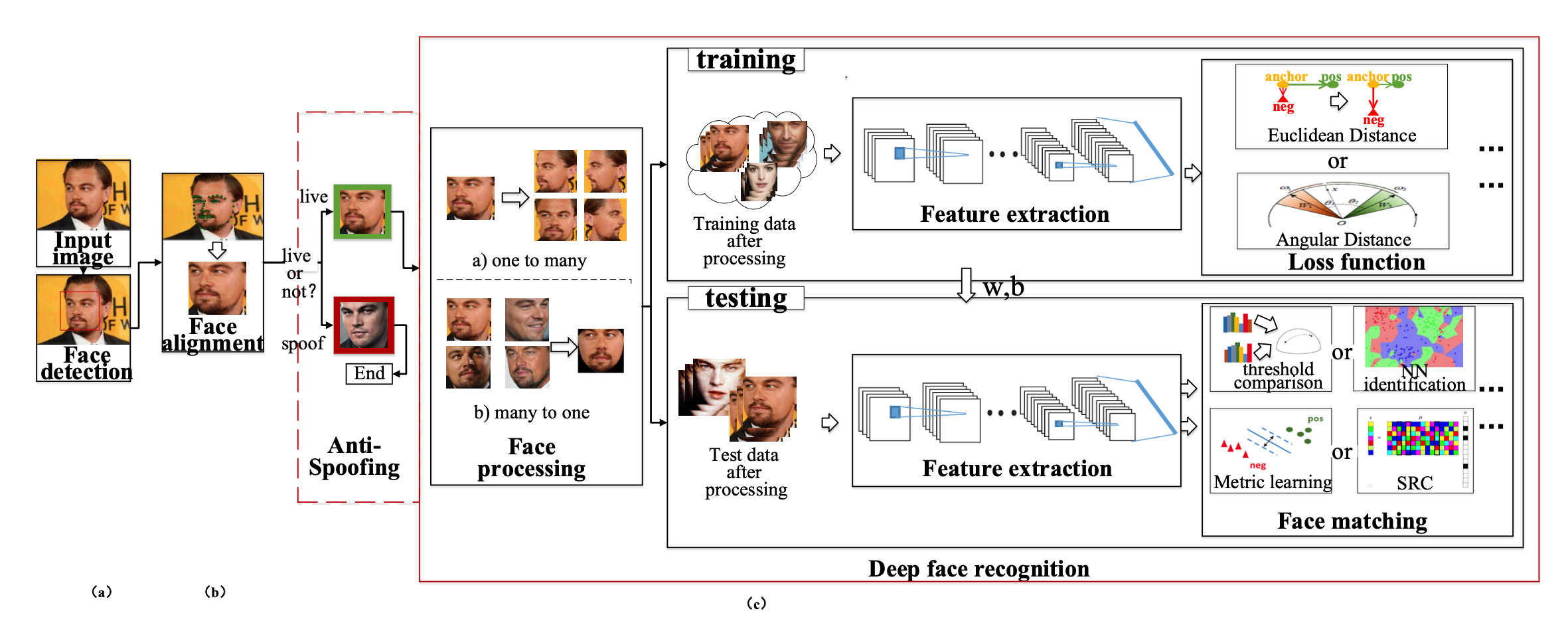
简介 一个完整的人脸识别系统包含以下几个模块 Face Detection: 人脸检测 Face Alignment:基于人脸关键点坐标对齐到正则坐标系下坐标 Face Recognition:基于对齐人脸进行识别 人脸识别的算法流程 人脸的识别流程:面部姿态处理(处理姿态,亮度,表情,遮挡),特征提取,人脸比对。 面部处理 face processing 这部分主要对姿态(主要)、亮度、表情、遮挡进行处理,可提升FR模型性能 主要包含两种处理方式: 1. "Onetomany Augmentation": 从单个图像生成不同姿态的图像,使模型学习到姿态不变性的表示 1. "Manytoone Normalization": 从多个不同姿态的图像中恢复人脸图像的标准视图 特征提取 Backb...
Reinforcement Learning
2026-01-11
引言 DDPG同样使用了ActorCritic的结构,Deterministic的确定性策略是和随机策略相对而言的,对于某一些动作集合来说,它可能是连续值,或者非常高维的离散值,这样动作的空间维度极大。如果我们使用随机策略,即像DQN一样研究它所有的可能动作的概率,并计算各个可能的动作的价值的话,那需要的样本量是非常大才可行的。于是有人就想出使用确定性策略来简化这个问题。 作为随机策略,在相同的策略,在同一个状态 s 处,采用的动作 [Math] 是基于一个概率分布的,即是不确定的。而确定性策略则决定简单点,虽然在同一个状态处,采用的动作概率不同,但是最大概率只有一个,如果我们只取最大概率的动作,去掉这个概率分布,那么就简单多了。即作为确定性策略,相同的策略,在同一个状态处,动作是唯一确定的...
Reinforcement Learning
2026-01-11
引言与背景 价值函数方法是强化学习中的核心技术,它解决了传统表格方法在处理大型状态或动作空间时的效率问题。本文探讨了从表格表示向函数表示的转变,这是强化学习算法发展的重要里程碑。 在强化学习的发展路径中,价值函数方法位于从基于模型到无模型、从表格表示到函数表示的演进过程中。它结合了时序差分学习的思想,并通过函数近似技术来处理复杂环境。 价值表示:从表格到函数 表格与函数表示的对比 传统的表格方法将状态值存储在一个表格中: 而函数近似方法则使用参数化函数来表示这些值,例如: [公式] 其中 [Math] 称作是状态 s 的特征向量, w 是参数向量。 两种不同的表现形式的区别主要体现在以下几个方面: 值的检索方式 值的更新方式 函数复杂度与近似能力 函数的复杂度决定了其近似的能力: 一阶线性函...
最优策略(Optimal Policy ) 之前在 贝尔曼方程中说过,状态值可以用来评估一个策略是好是坏,这里给出正式的概念: [公式] 那么此时 [Math] 比 [Math] ”更好“ 最优状态值(Optimal State Value): 最优策略(Optimal Policy): 性质: 为了说明上述性质, 我们研究贝尔曼最优方程 Bellman optimality equation(BOE) 贝尔曼最优方程(BOE) 定义 分析最优策略和最优状态值的工具是贝尔曼最优方程(BOE)。通过求解此方程,我们可以获得最优策略和最优状态值。 对于每个 s∈S ,BOE 的elementwise表达式为: [公式] 其中, v(s) 和 [Math] 是待求解的未知变量, π(s) 表示状态...
Reinforcement Learning
2026-01-11
概述与理论背景 ActorCritic方法是强化学习中的一类重要算法,它巧妙地结合了基于策略(policybased)和基于价值(valuebased)的方法。在这种结构中,"Actor"指策略更新步骤,负责根据策略执行动作;而"Critic"指价值更新步骤,负责评估Actor的表现。从另一个角度看,ActorCritic方法本质上仍是策略梯度算法,可以通过扩展策略梯度算法获得。 ActorCritic方法在强化学习中的位置非常重要,它既保留了策略梯度方法直接优化策略的优势,又利用了值函数方法的效率。这种结合使得ActorCritic方法成为解决复杂强化学习问题的强大工具。 最简单的ActorCritic算法(QAC) QAC算法通过扩展策略梯度方法得到。策略梯度方法的核心思想是通过最大化标...
Reinforcement Learning
2026-01-11
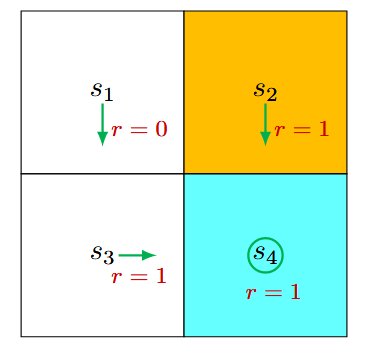
状态价值(State values) 定义 状态价值是强化学习中的核心概念,用于衡量Agent从某个状态出发、遵循特定策略后所能获得的期望回报。 数学表达为: [公式] 其中: [Math] :状态 s 的状态价值函数(statevalue function) 或者简称为 状态价值(state value); [Math] :智能体遵循的策略; [Math] :从当前时间步 t 开始的折扣回报; [Math] :折扣因子,用于平衡即时奖励和未来奖励。 状态价值的特点 依赖于状态 s :状态价值是条件期望,条件是智能体从状态 s 开始。 依赖于策略 [Math] :不同策略会生成不同的轨迹,从而影响状态价值。 与时间步无关:状态价值是一个固定值,与当前时间步 t 无关。 代表一个状态的价值。如...
Algorithm
2026-01-11
题目 给定一个无序的数组,找出数组在排序之后,相邻元素之间最大的差值。 如果数组元素个数小于 2,则返回 0。 Example 1: [代码] 解题思路:如果进行排序,这里会超时。采用桶排序 排序算法 的思想,可以在线性时间解决。 1. 首先建立桶,每个桶中只需要存放这个桶中元素的最大值和最小值。 1. 我们期望将数组中的各个数等距离分配,也就是每个桶的长度相同,也就是对于所有桶来说,桶内最大值减去桶内最小值都是一样的。可以当成公式来记。 1. 确定桶的数量,最后的加一保证了数组的最大值也能分到一个桶。为什么需要这样规定桶的尺寸呢?因为这样可以让最大的间距的两个元素在两个不同的桶中。可以证明一下,因为我们用元素范围之差除以元素个数,所以桶的尺寸就是平均的元素间距,显然最大间距的两个元素不可能...
Algorithm
2026-01-11
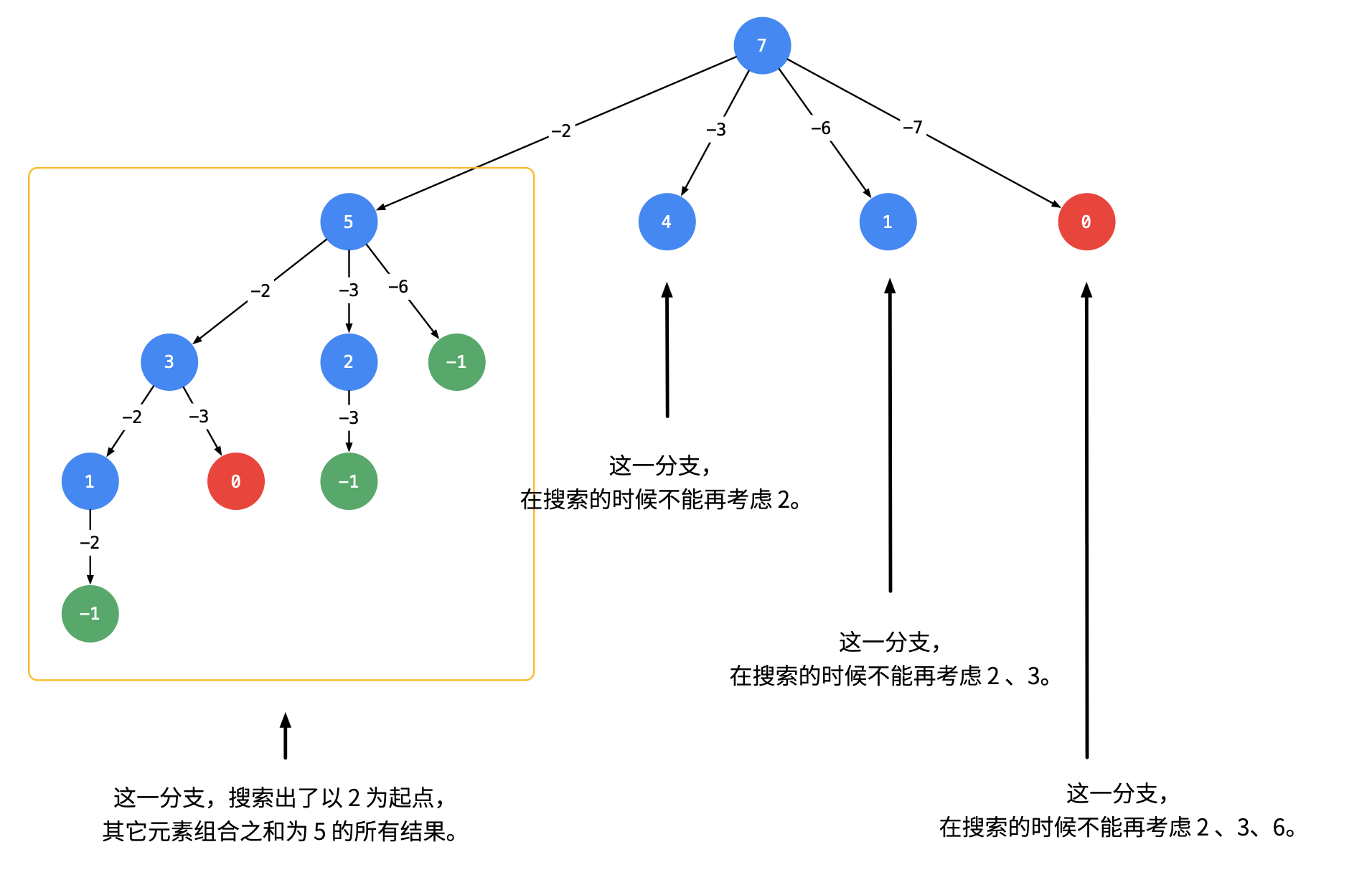
1. 可以重复选取 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的数字可以无限制重复被选取。 画出树状搜索图如下, 为了去除重复的情况, 我们需要按照某种顺序搜索,具体做法是:每一次搜索的时候,设置下一轮搜索的起点 [代码] 2. 不能被重复选取 与上面的区别在于 1. index每次不要重复搜索,而是去寻找下一个 1. 排除重复的元素 [代码]
Large Model
2026-01-11
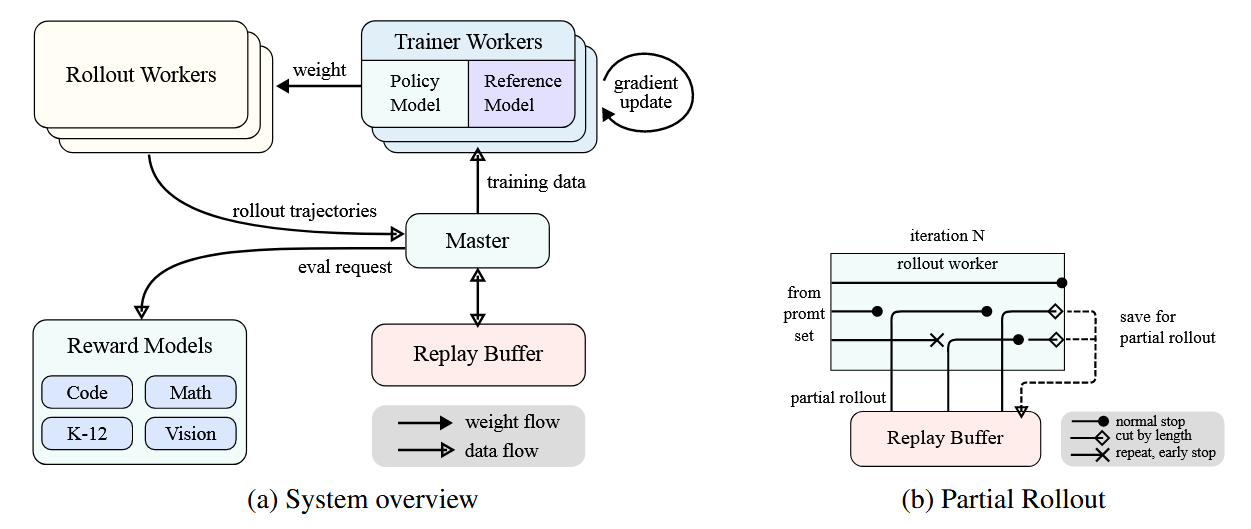
概述 Kimi k1.5采用了一种简化而有效的强化学习框架,其核心在于长上下文扩展和改进的策略优化方法,而不依赖于更复杂的技术如蒙特卡洛树搜索、价值函数和过程奖励模型。 问题设定 给定训练数据集 D = \{(x_i, y^_i)\}_{i=1}^n ,其中包含问题 x_i 和对应的真实答案 y^_i ,目标是训练一个策略模型 [Math] 来准确解决测试问题。在复杂推理场景中,思维链(CoT)方法提出使用一系列中间步骤 z = (z_1, z_2, ..., z_m) 来连接问题 x 和答案 y ,每个 z_i 是解决问题的重要中间步骤。 当解决问题 x 时,思维 [Math] 被自回归采样,最终答案 [Math] 。 强化学习目标 基于真实答案 y^ ,分配一个值 [Math] , Ki...
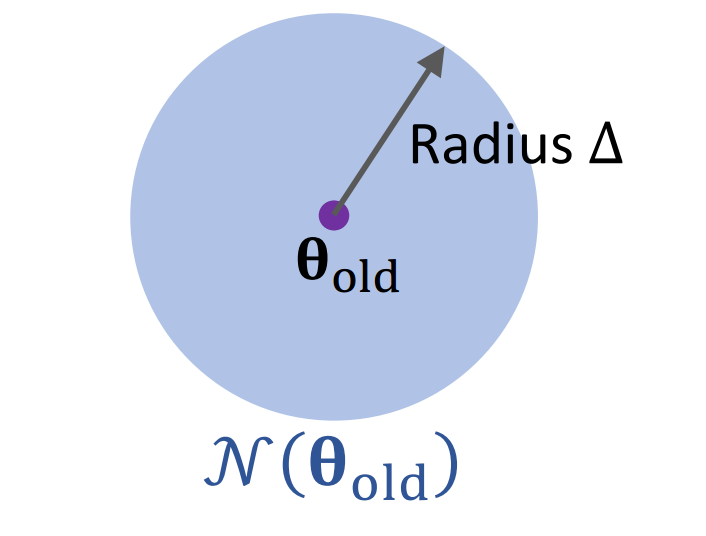
💡 引言 Trust Region Policy Optimization (TRPO) 是2015年的ICML会议上提出的一种强大的基于策略的强化学习算法。TRPO 解决了传统策略梯度方法中的一些关键问题,特别是训练不稳定和步长选择困难的问题。与传统策略梯度算法相比,TRPO 具有更高的稳健性和样本效率,能够在复杂环境中取得更好的性能。 优化基础 在深入了解 TRPO 之前,我们需要先简单回顾一些优化方法的基础知识。 梯度上升法 梯度上升法是一种迭代优化算法,用于寻找函数的局部最大值。 目标:找到使目标函数 [Math] 最大化的参数 [Math] : [公式] 梯度上升迭代过程: 1. 在当前参数 [Math] 处计算梯度: [Math] 1. 更新参数: 梯度上升法的主要问题是学习率的...
Reinforcement Learning
2026-01-11
引言 时序差分(TemporalDifference,TD)方法是强化学习中的一类核心算法,它结合了动态规划与蒙特卡洛方法的优点。TD方法是无模型(modelfree)学习方法,不需要环境模型即可学习价值函数和最优策略。 TD方法的核心特点是通过比较不同时间步骤的估计值之间的差异来更新价值函数,这种差异被称为"时序差分误差"(TD error)。TD方法可以被视为解决贝尔曼方程或贝尔曼最优方程的特殊随机逼近算法。 基础TD算法:状态值函数学习 给定策略 [Math] ,基础TD算法用于估计状态值函数 [Math] 。假设我们有一些按照策略 [Math] 生成的经验样本 (s_0, r_1, s_1, ..., s_t, r_{t+1}, s_{t+1}, ...) ,TD算法的更新规则为: ...