INCOMING TRANSMISSION

问题定义 多元二次多项式，维度为 n ，那么可以用以下公式描述该函数： [Formula] 其中 a_{i,j} 为二次项系数，共有 n^2 项， 1≤i,j≤n ，且所有的 a 不全为0，即 ∃a_{i,j}≠0 ; b_k 为一次项系数，共 n 项， 1≤k≤n ; c 为常数项。 记 f(x)=[x_1,x_2,...,x_n]^T ，则上述函数可以写作二次型的形式： 转化过程中A,b满足： A 为n阶对称方阵， A_{i,j}=a_{i,j} 因为 ∃a_{i,j}≠0 ，A不为零矩阵 b_i=b_i 为了后续计算简便，我们将二次型稍作改动： [Formula] 我们的目标就是寻找该函...

基本概念 方向导数：是一个数；反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。 偏导函数：是一个函数；是一个关于点的偏导数的函数。 梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。 方向导数 反映的是 f(x,y) 在 P_0 点沿方向 v 的变化率。 例子如下： 题目 设二元函数 f(x, y) = x^2 + y^2 ，分别计算此函数在点 (1, 2) 沿方向 w=\{3, 4\} 与方向 u=\{1, 0\} 的方向导数。 解： ...

一、IOU(Intersection over Union) 1. 特性(优点) IoU就是我们所说的交并比，是目标检测中最常用的指标，在anchorbased的方法中，他的作用不仅用来确定正样本和负样本，还可以用来评价输出框（predict box）和groundtruth的距离。 1. 可以说它可以反映预测检测框与真实检测框的检测效果。 1. 还有一个很好的特性就是尺度不变性，也就是对尺度不敏感（scale invariant）， 在regression任务中，判断predict box和gt的距离最直接的指标就是IoU。(满足非负性；同一性；对称性；三角不等性) [代码] 2. 作为损失函数会出现的问题(缺点) 1. 如果两个框没有相交，根据定义，IoU=0，不能反映两者的距离大小（重...

Introduction 目标检测中NMS需要依据候选检测目标的排序来进行筛选框，如果分类得分较低，但是定位框准确会导致在NMS中将该bbox框被排除掉，因此这个排序的可靠性就非常重要。之前的工作主要采用IOU分支（IOUNet）与Centerness得分（FCOS）来作为大量候选检测的排序依据。 然而，本文认为这些方法可以有效缓解分类得分和物体定位精度之间的不对齐问题。 但是，它们是次优解的，因为将两个不完善的预测相乘可能会导致排名依旧变差，作者经过试验表明，通过这种方法实现的性能上限非常有限。 此外，增加一个额外的网络分支来预测定位分数并不是一个很好的解决方案，并且会带来额外的计算负担。 基于上述分析，作者提出：不采用预测一个额外的定位精确度得分（IOUaware Centerness）...

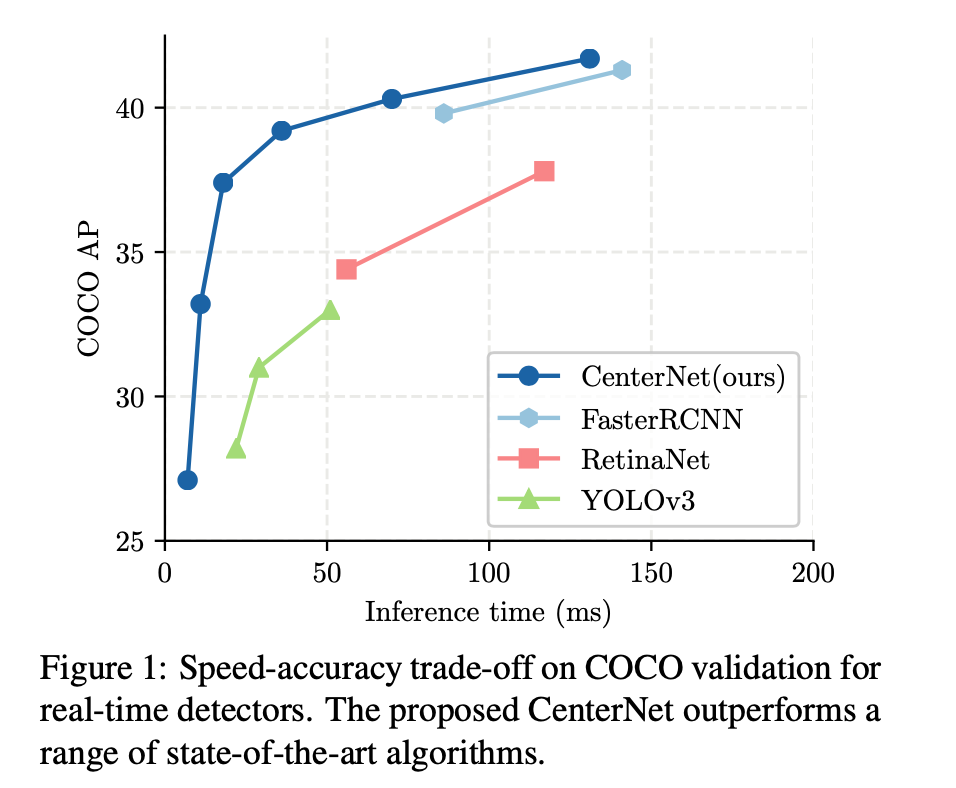
前言 anchorfree目标检测属于anchorfree系列的目标检测，相比于CornerNet做出了改进，使得检测速度和精度相比于onestage和twostage的框架都有不小的提高，尤其是与YOLOv3作比较，在相同速度的条件下，CenterNet的精度比YOLOv3提高了4个左右的点。 CenterNet不仅可以用于目标检测，还可以用于其他的一些任务，如肢体识别或者3D目标检测等等。 那CenterNet相比于之前的onestage和twostage的目标检测有什么特点？ CenterNet的“anchor”仅仅会出现在当前目标的位置处而不是整张图上撒，所以也没有所谓的box overlap大于多少多少的算positive anchor这一说，也不需要区分这个anchor是物体还是...

题目 给定一个无序的数组，找出数组在排序之后，相邻元素之间最大的差值。 如果数组元素个数小于 2，则返回 0。 Example 1: [代码] 解题思路：如果进行排序，这里会超时。采用桶排序 排序算法 的思想，可以在线性时间解决。 1. 首先建立桶，每个桶中只需要存放这个桶中元素的最大值和最小值。 1. 我们期望将数组中的各个数等距离分配，也就是每个桶的长度相同，也就是对于所有桶来说，桶内最大值减去桶内最小值都是一样的。可以当成公式来记。 1. 确定桶的数量，最后的加一保证了数组的最大值也能分到一个桶。为什么需要这样规定桶的尺寸呢？因为这样可以让最大的间距的两个元素在两个不同的桶中。可以证明一下，因为我们用元素范围之差除以元素个数，所以桶的尺寸就是平均的元素间距，显然最大间距的两个元素不可能...

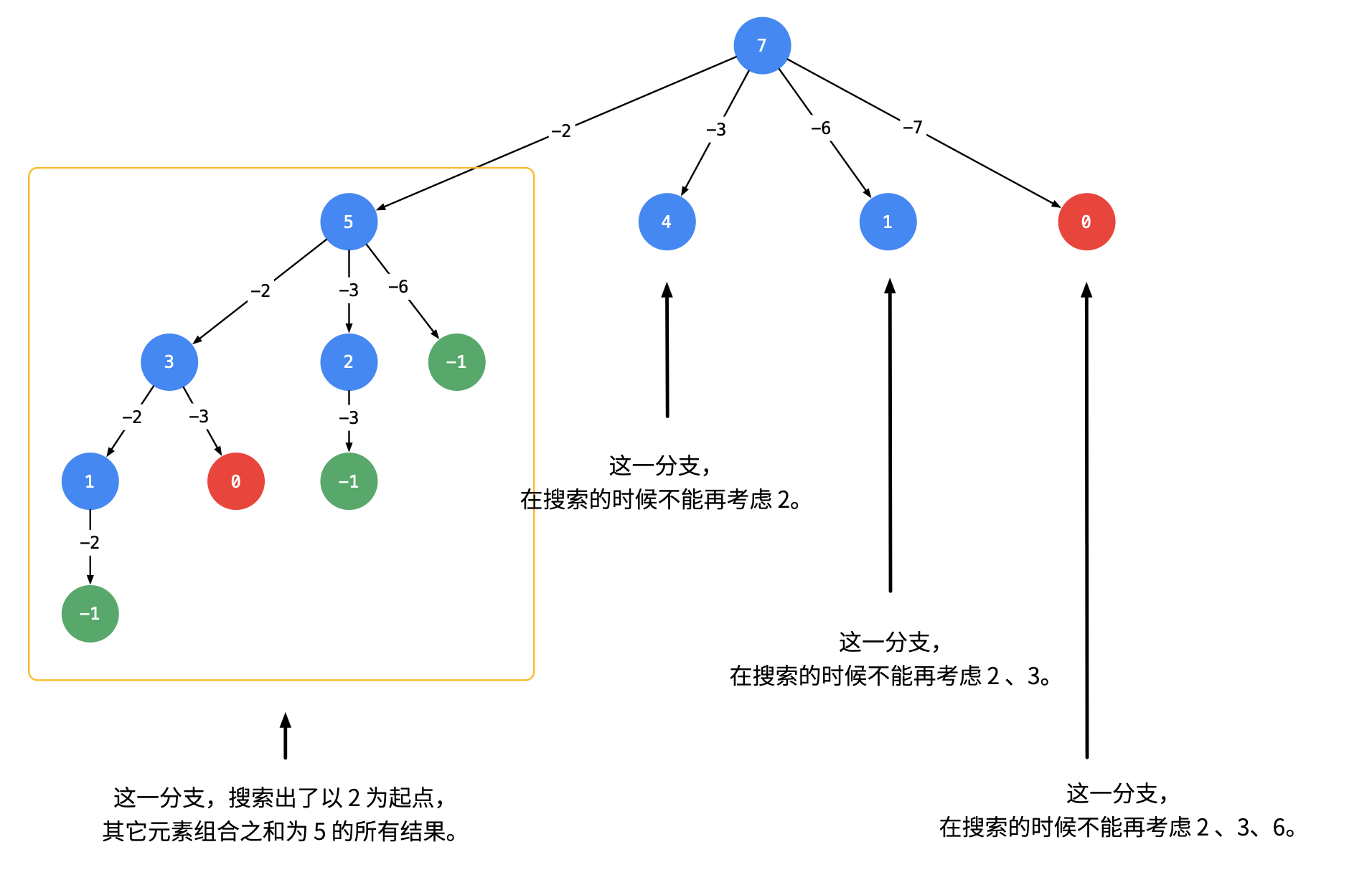
1. 可以重复选取 给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的数字可以无限制重复被选取。 画出树状搜索图如下， 为了去除重复的情况， 我们需要按照某种顺序搜索，具体做法是：每一次搜索的时候，设置下一轮搜索的起点 [代码] 2. 不能被重复选取 与上面的区别在于 1. index每次不要重复搜索，而是去寻找下一个 1. 排除重复的元素 [代码]

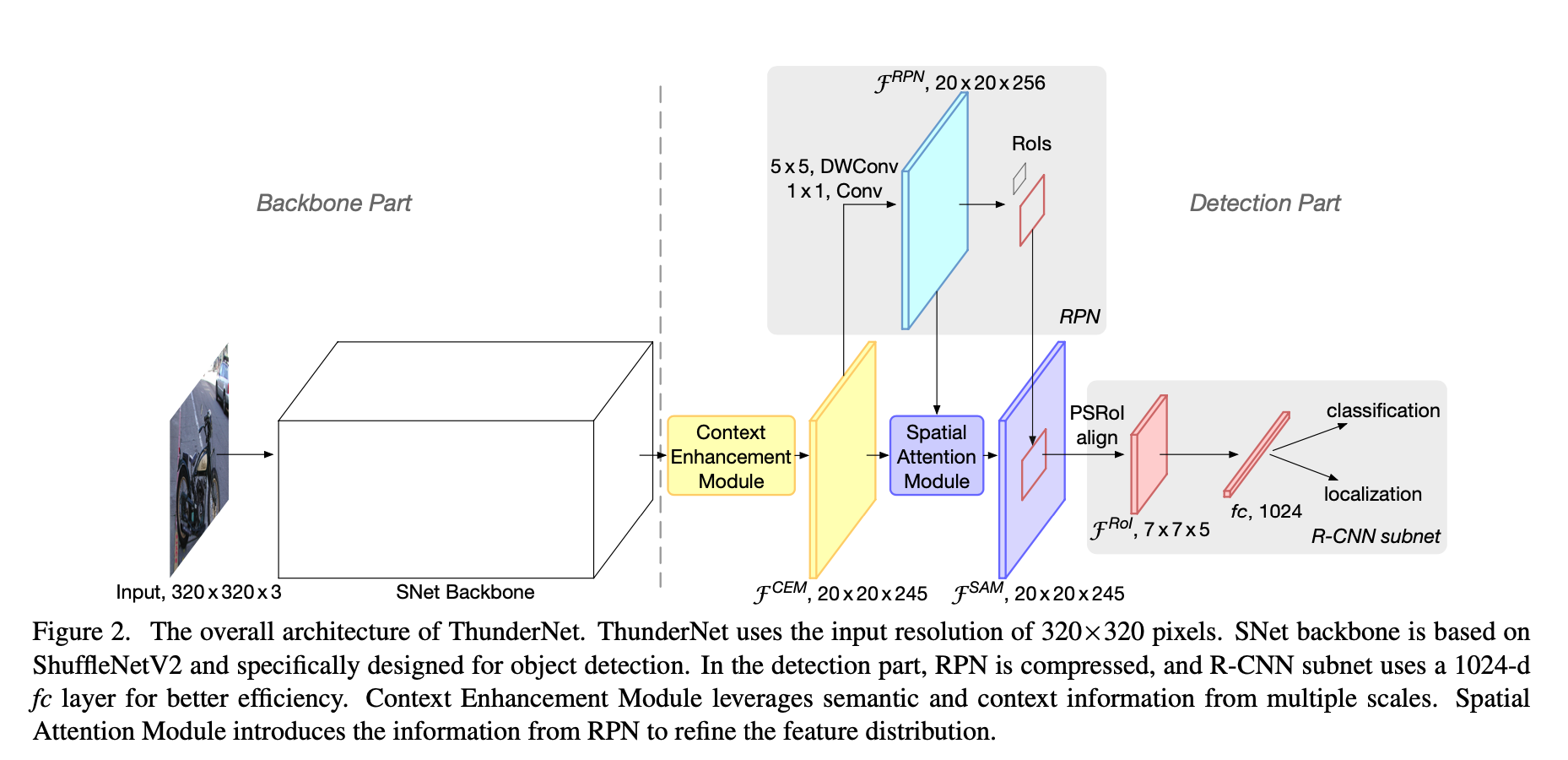
网络整体介绍 ThunderNet的整体架构如下图所示。 ThunderNet使用320×320像素作为网络的输入分辨率。整体的网络结构分为两部分：Backbone部分和Detection部分。网络的骨干部分为SNet，SNet是基于ShuffleNetV2进行修改得到的。 网络的检测部分，利用了压缩的RPN网络，修改自LightHead RCNN网络用以提高效率。 并提出Context Enhancement Module整合局部和全局特征增强网络特征表达能力。 并提出Spatial Attention Module空间注意模块，引入来自RPN的前后景信息用以优化特征分布。 backbone 部分 1.输入分辨率 为了加快推理（前向操作）速度，作者使用320320大小的输入图像。需要注意的...

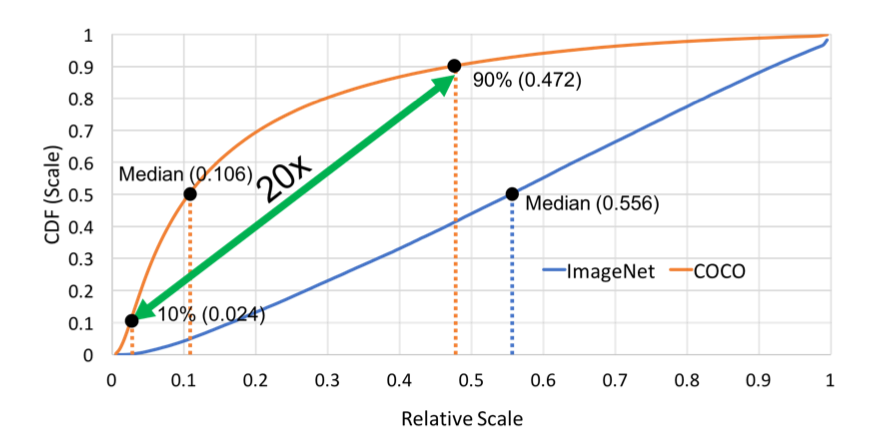
1. 检测任务的困难 图像分类算法，比如ResNeXt101 32 × 48d网络结构，在Imagenet数据集上的Top5准确率已经98%左右，Top1为85%。对于图像检测算法，最好的模型在coco数据集上的效果 AP_{50} 为62%，显然，总体上来看，准确率差了20个点左右，那么问题来了，为什么检测算法比识别算法的效果低这么多呢？ 1.1 尺度差异 作者认为原因在于，检测任务中的目标存在较大的尺度变化（large scale variation）。作者统计了Imagenet和COCO数据集的特点，如下图， 其中，横坐标表示目标相对于原图的比例，纵坐标表示累计分布（cumulation distribution function）。显然，由图中可以看出，COCO数据集中50%的目标相...

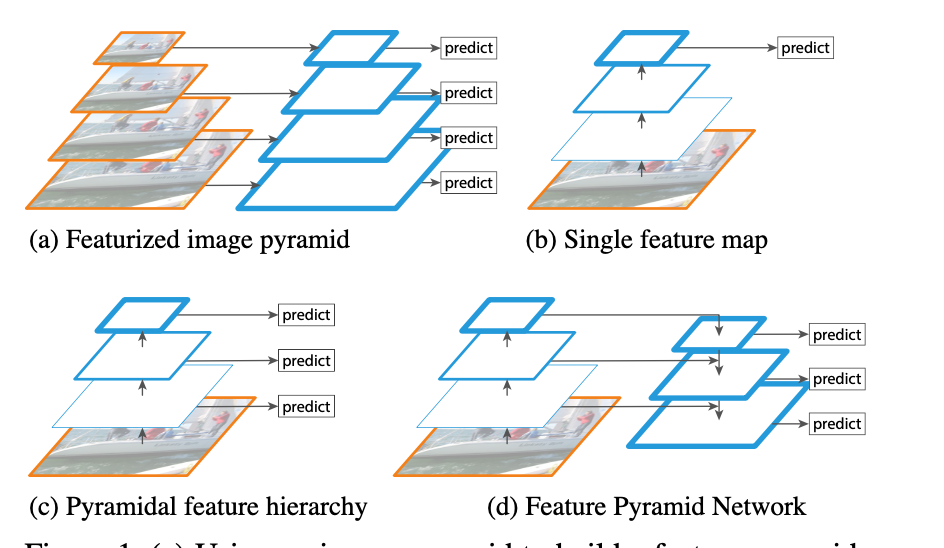
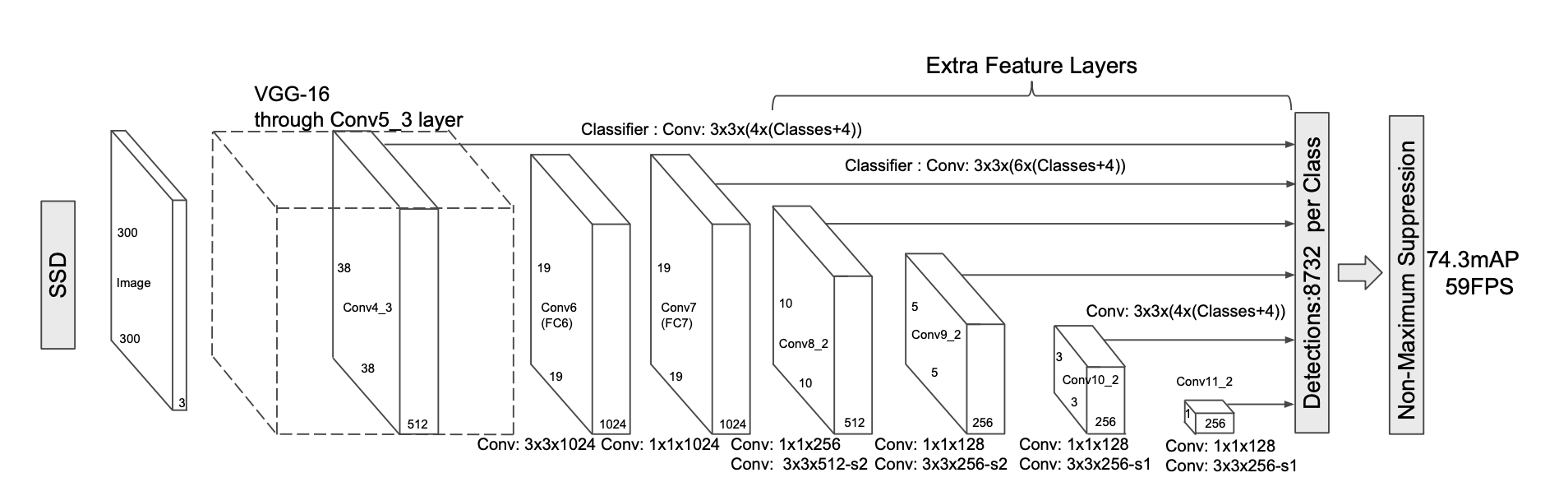
FPN 1.结构区别 （a）图片金字塔生成特征金字塔：缩放图片比例 （b）通常的CNN网络结构 （c）多尺度特征融合的方式：像SSD（Single Shot Detector）就是采用这种多尺度特征融合的方式，没有上采样过程，即从网络不同层抽取不同尺度的特征做预测，这种方式不会增加额外的计算量。作者认为SSD算法中没有用到足够低层的特征（在SSD中，最低层的特征是VGG网络的conv4_3），而在作者看来足够低层的特征对于检测小物体是很有帮助的。 （d）FPN：这是本文要讲的网络，FPN主要解决的是物体检测中的多尺度问题，通过简单的网络连接改变，在基本不增加原有模型计算量的情况下，大幅度提升了小物体检测的性能。通过高层特征进行上采样和低层特征进行自顶向下的连接，而且每一层都会进行预测。 2....

一、传统的图像金字塔 最开始在深度学习方法流行之前，对于不同尺度的目标，大家普遍使用将原图构建出不同分辨率的图像金字塔，再对每层金字塔用固定输入分辨率的分类器在该层滑动来检测目标，以求在金字塔底部检测出小目标；或者只用一个原图，在原图上，用不同分辨率的分类器来检测目标，以求在比较小的窗口分类器中检测到小目标。经典的基于简单矩形特征(Haar)+级联Adaboost与Hog特征+SVM的DPM目标识别框架，均使用图像金字塔的方式处理多尺度目标，早期的CNN目标识别框架同样采用该方式，但对图像金字塔中的每一层分别进行CNN提取特征，耗时与内存消耗均无法满足需求。但该方式毫无疑问仍然是最优的。值得一提的是，其实目前大多数深度学习算法提交结果进行排名的时候，大多使用多尺度测试。同时类似于SNIP使用...

SoftNMS/DIoUNMS softnms参考： SoftNMS 可以看到，SoftNMS与传统NMS的区别在于对score分数调整的处理。如果是传统的NMS操作，那么当 B 中的 b_i 和 [Math] 的IoU值大于阈值 N_t ，那么就从 B 和 S 中去除该box；对于SoftNMS而言是先计算 [Math] 与 b_i 的IoU，然后IoU经过一个函数输出最后与 s_i 相乘最终得到box的分数。 其中 s_i 的score遵循IoU越大，分数越低的原则（IoU越大，越可能是背景），所以 s_i 定义如下： 考虑到上式是不连续的，并且当达到N_t的NMS阈值时会施加突然的惩罚， 如果惩罚函数是连续的，那将是理想的，否则它可能导致检测结果的排序列表的突然改变（集合D中的scor...