INCOMING TRANSMISSION

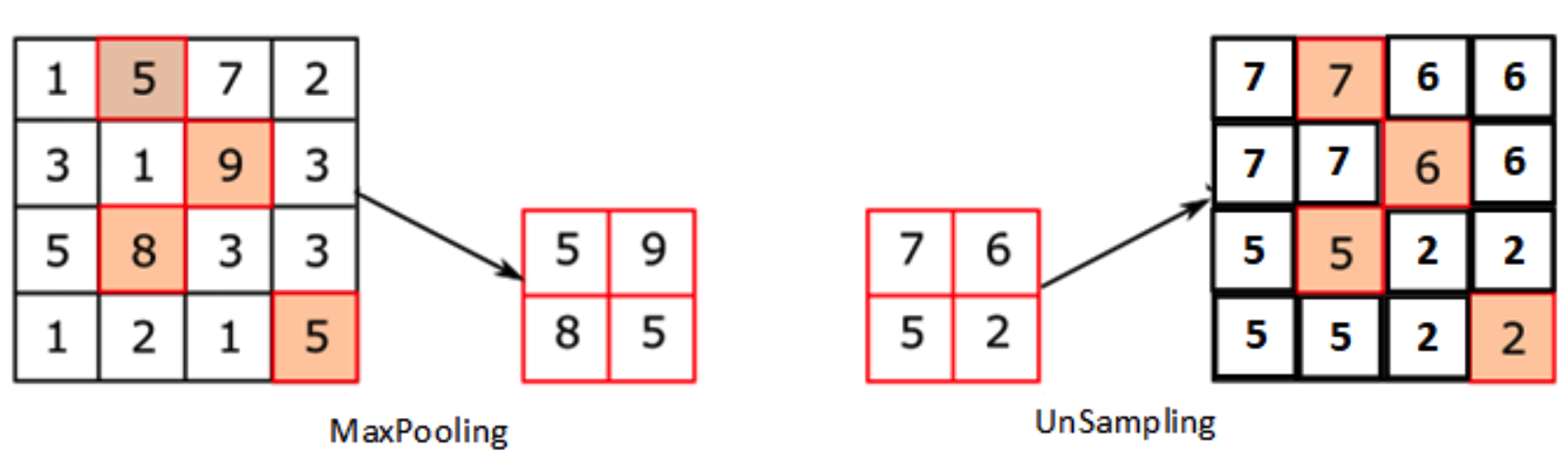
通过卷积和池化等技术可以将图像进行降维，因此，一些研究人员也想办法恢复原分辨率大小的图像，特别是在语义分割领域应用很成熟。 1、Upsampling（上采样）[没有学习过程] 在FCN、Unet等网络结构中，涉及到了上采样。上采样概念：上采样指的是任何可以让图像变成更高分辨率的技术。最简单的方式是重采样和插值：将输入图片进行rescale到一个想要的尺寸，而且计算每个点的像素点，使用如双线性插值等插值方法对其余点进行插值来完成上采样过程。 在PyTorch中，上采样的层被封装在torch.nn中的Vision Layers里面，一共有4种： PixelShuffle Upsample UpsamplingNearest2d UpsamplingBilinear2d 0）PixelShuffl...

论文地址： 🔖 https://arxiv.org/pdf/2107.11291 代码地址： 前言 一般来说，我们可以把姿态估计任务分成两个流派：Heatmapbased和Regressionbased。 其主要区别在于监督信息的不同，Heatmapbased方法监督模型学习的是高斯概率分布图，即把GroundTruth中每个点渲染成一张高斯热图，最后网络输出为K张特征图对应K个关键点，然后通过argmax或softargmax来获取最大值点作为估计结果。这种方法由于需要渲染高斯热图，且由于热图中的最值点直接对应了结果，不可避免地需要维持一个相对高分辨率的热图（常见的是64x64，再小的话误差下界过大会造成严重的精度损失），因此也就自然而然导致了很大的计算量和内存开销。 Regression...

🔖 https://stability.ai/news/stablediffusion3researchpaper 概述 SD3 模型与训练策略改进细节 SD3除了将去噪网络从 UNet 改成 DiT 外，SD3 还在模型结构与训练策略上做了很多小改进： 改变训练时噪声采样方法 将一维位置编码改成二维位置编码 提升 VAE 隐空间通道数 对注意力 QK 做归一化以确保高分辨率下训练稳定 本文会简单介绍这些改进。 论文阅读 核心贡献 介绍 Stable Diffusion 3 (SD3) 的文章标题为 Scaling Rectified Flow Transformers for HighResolution Image Synthesis。与其说它是一篇技术报告，更不如说它是一篇论文，因为它...

引言与背景 价值函数方法是强化学习中的核心技术，它解决了传统表格方法在处理大型状态或动作空间时的效率问题。本文探讨了从表格表示向函数表示的转变，这是强化学习算法发展的重要里程碑。 在强化学习的发展路径中，价值函数方法位于从基于模型到无模型、从表格表示到函数表示的演进过程中。它结合了时序差分学习的思想，并通过函数近似技术来处理复杂环境。 价值表示：从表格到函数 表格与函数表示的对比 传统的表格方法将状态值存储在一个表格中： 而函数近似方法则使用参数化函数来表示这些值，例如： [公式] 其中 [Math] 称作是状态 s 的特征向量， w 是参数向量。 两种不同的表现形式的区别主要体现在以下几个方面： 值的检索方式 值的更新方式 函数复杂度与近似能力 函数的复杂度决定了其近似的能力： 一阶线性函...

概述 问题定义 广义的 Gaze Estimation 泛指与眼球、眼动、视线等相关的研究，因此有不少做 saliency 和 egocentric 的论文也以 gaze 为关键词。而本文介绍的 Gaze Estimation 主要以眼睛图像或人脸图像为处理对象，估算人的视线方向或注视点位置， 如下图所示。 gaze角度的表示一般使用一个3d向量作为表示，也可以转换为pitch 和yaw角度，具体可参考 Model Gaze模型一般使用回归模型，所以这里基本只介绍一些在gaze model中使用的小技巧 Rle Loss 实际问题

引言 时序差分（TemporalDifference，TD）方法是强化学习中的一类核心算法，它结合了动态规划与蒙特卡洛方法的优点。TD方法是无模型（modelfree）学习方法，不需要环境模型即可学习价值函数和最优策略。 TD方法的核心特点是通过比较不同时间步骤的估计值之间的差异来更新价值函数，这种差异被称为"时序差分误差"（TD error）。TD方法可以被视为解决贝尔曼方程或贝尔曼最优方程的特殊随机逼近算法。 基础TD算法：状态值函数学习 给定策略 [Math] ，基础TD算法用于估计状态值函数 [Math] 。假设我们有一些按照策略 [Math] 生成的经验样本 (s_0, r_1, s_1, ..., s_t, r_{t+1}, s_{t+1}, ...) ，TD算法的更新规则为： ...