INCOMING TRANSMISSION

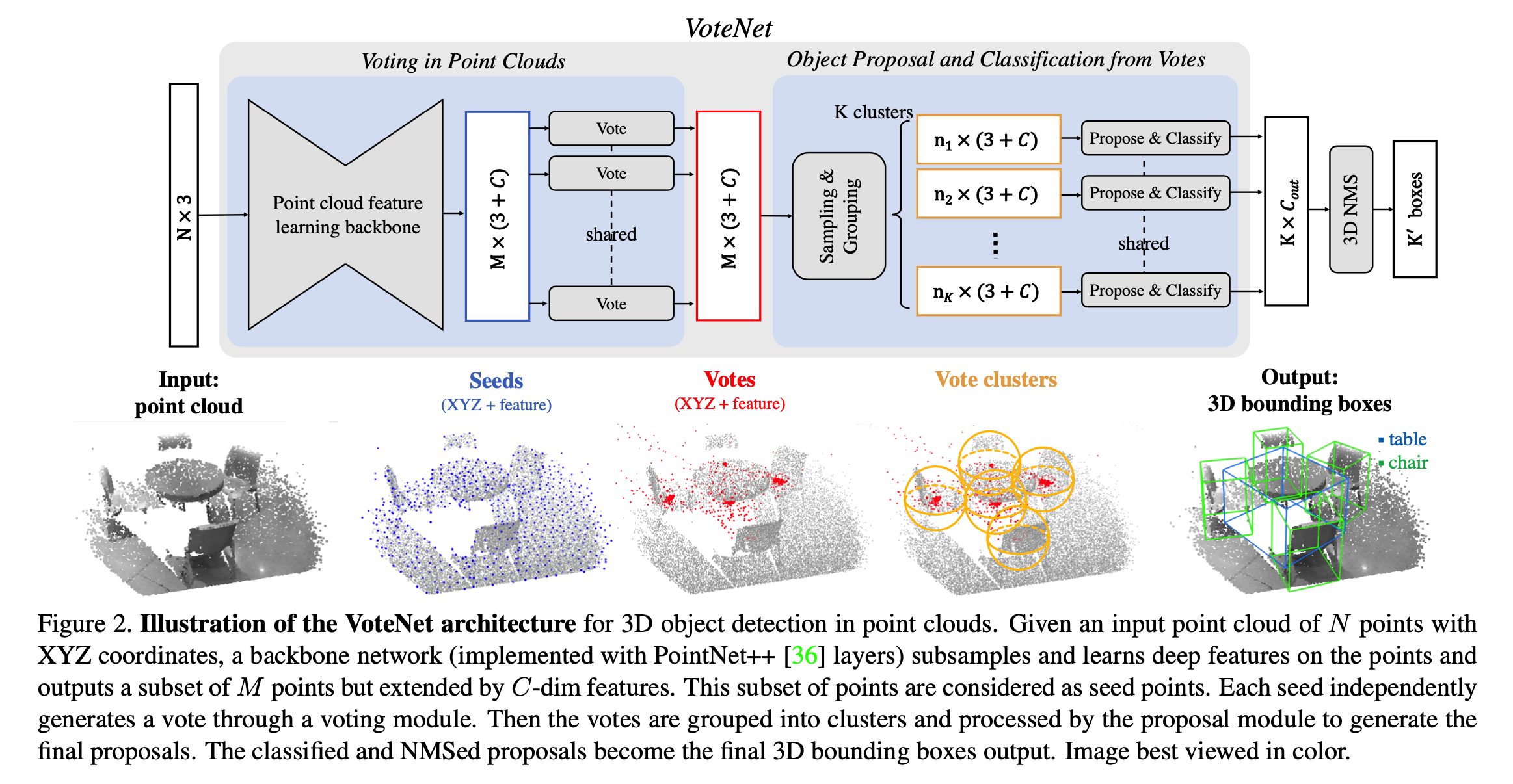
Hough Voting 本文的标题是Deep Hough Voting，先来说一下Hough Voting。 用Hough变换检测直线大家想必都听过：对于一条直线，可以使用(r, θ)两个参数进行描述，那么对于图像中的一点，过这个点的直线有很多条，可以生成一系列的(r, θ)，在参数平面内就是一条曲线，也就是说，一个点对应着参数平面内的一个曲线。那如果有很多个点，则会在参数平面内生成很多曲线。那么，如果这些点是能构成一条直线的，那么这条直线的参数(r, θ)就在每条曲线中都存在，所以看起来就像是多条曲线相交在（r,θ）。可以用多条曲线投票的方式来看，其他点都是很少的票数，而（r,θ）则票数很多，所以直线的参数就是（r,θ）。 所以Hough变换的思想就是在于，在参数空间内进行投票，投票得数...

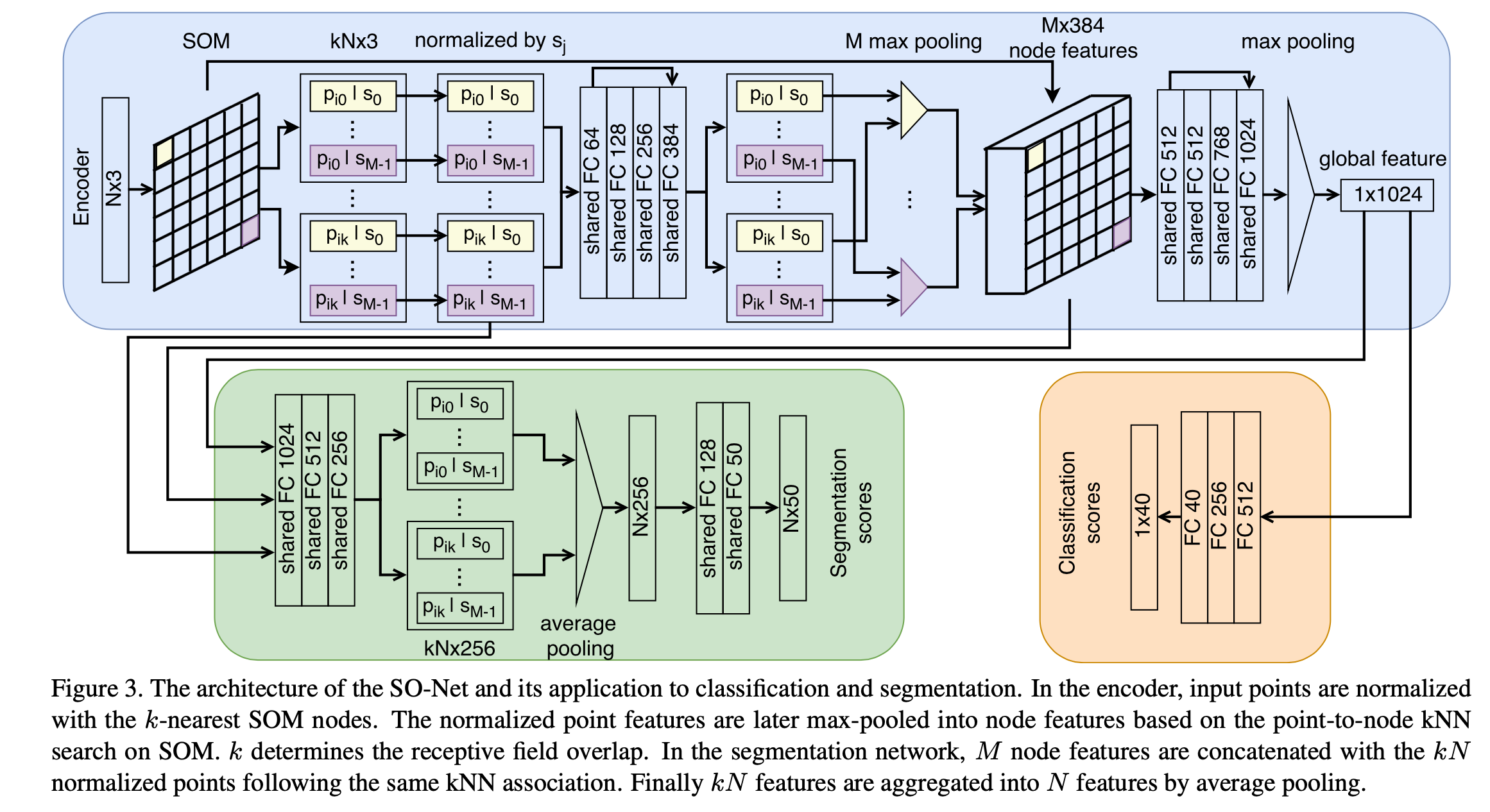
概括 针对一些网络在处理point cloud时的缺点，如：不能对点的空间分布进行建模（例如PointNet++，只是能获取局部信息不能得到局部区域之间的空间关系），提出了SONet。SO的含义是利用Selforganizing map的Net。 结果：它具有能够对点的空间分布进行建模、层次化特征提取、可调节的感受野范围的优点，并能够用于多种任务如重建、分类、分割等等。取得了相似或超过SOTA的性能，因为可并行化和架构简单使得训练速度很快。 贡献： TODO IDEA：作者发现将CNN直接用于SOM图上性能不升反降，为什么（推测：可能是SOM的2D map并不是保持了原本的空间对应关系，可能nodes之间是乱序的，导致用conv2d时精度反而降低）？ 难点 如何对local regions之...

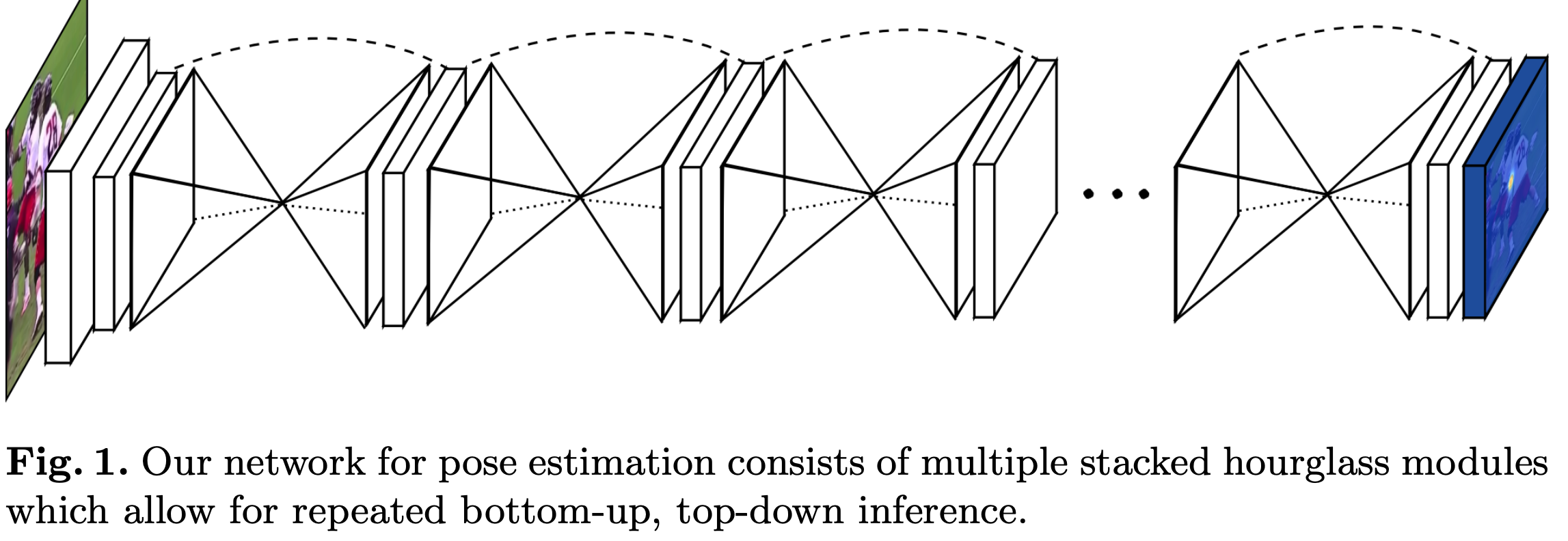
论文介绍了一种新的网络结构用于人体姿态检测，作者在论文中展现了不断重复bottomup、topdown过程以及运用intermediate supervison（中间监督）对于网络性能的提升，下面来介绍Stacked Hourglass Networks. 简介 理解人类的姿态对于一些高级的任务比如行为识别来说特别重要，而且也是一些人机交互任务的基础。作者提出了一种新的网络结构Stacked Hourglass Networks来对人体的姿态进行识别，这个网络结构能够捕获并整合图像所有尺度的信息。之所以称这种网络为Stacked Hourglass Networks，主要是它长得很像堆叠起来的沙漏，如下图所示： 这种堆叠在一起的Hourglass模块结构是对称的，bottomup过程将图片从...

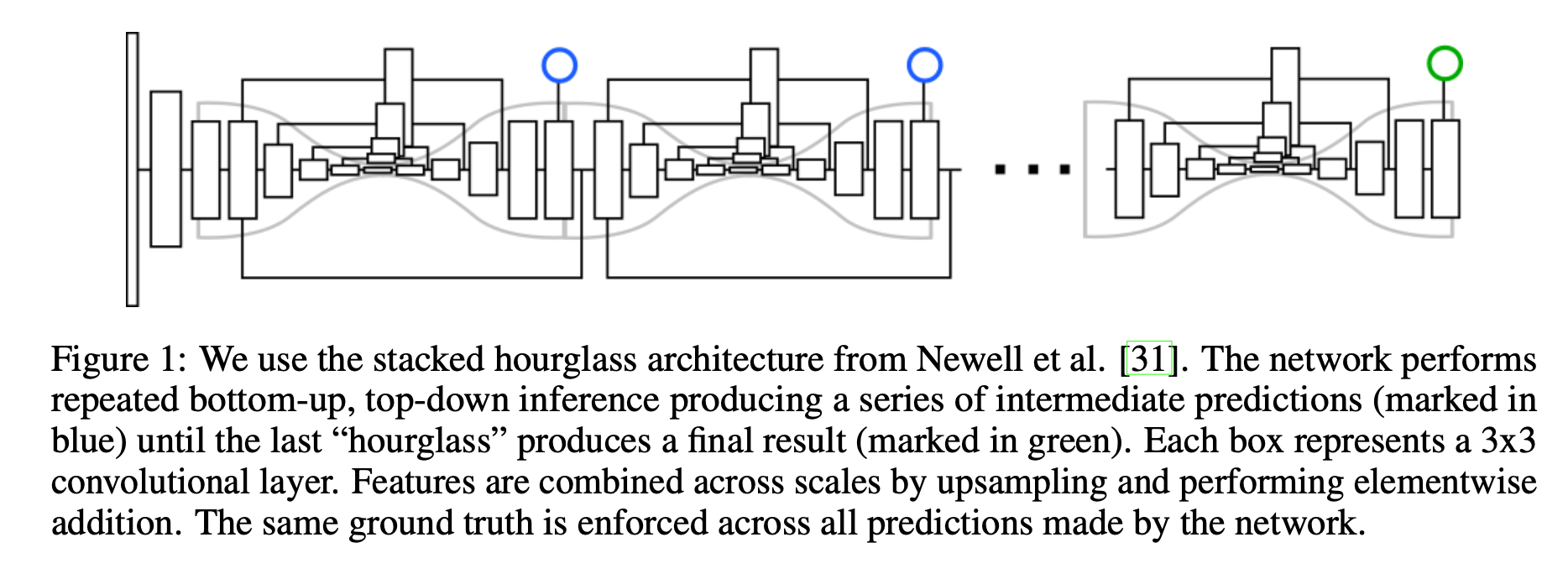
简介 作者认为许多计算机视觉的任务可以看作是检测和分组问题检测一些小的单元，然后将它们组合成更大的单元，例如，多人目标检测可以通过检测人的关节点然后再将它们进行分组（属于同一个人的关节点为一组）解决；实例分割问题可以看作是检测一些相关的像素然后将它们组合成一个目标实例。 Associative Embedding是一种表示关节检测和分组任务的输出的新方法，其基本思想是为每次检测引入一个实数，用作识别对象所属组的“tag”，换句话说，标签将每个检测与同一组中的其他检测相关联。作者使用一个损失函数使得如果相应的检测属于ground truth中的相同组则促使这一对标签具有相似的值。需要注意的是，这里标签具体的值并不重要，重要的是不同标签之间的差异。 这篇其实是源自Stacked Hourglas...

整体流程： [代码] 0. 数据预处理 这个步骤主要是crop四路数据，及生成后续步骤所需要的yaml文件。 1. 四路相机与双路相机标定 内参标定 [代码] 这里主要的函数就是： pts = cv2.findChessboardCorners(img, (board_width, board_height))[1] cv2.cornerSubPix(gray, pts, (12, 12), (1, 1), (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_COUNT, 30, 0.1)) det, intr, dist, _, _ = cv2.calibrateCamera(obj_pts, img_pts, self.imgSize, None, No...

梯度检查点（Gradient Checkpointing） 大模型的参数量巨大，即使将batch_size设置为1并使用梯度累积的方式更新，也仍然会OOM。原因是通常在计算梯度时，我们需要将所有前向传播时的激活值保存下来，这消耗大量显存。 还有另外一种延迟计算的思路，丢掉前向传播时的激活值，在计算梯度时需要哪部分的激活值就重新计算哪部分的激活值，这样做倒是解决了显存不足的问题，但加大了计算量同时也拖慢了训练。 梯度检查点（Gradient Checkpointing）在上述两种方式之间取了一个平衡，这种方法采用了一种策略选择了计算图上的一部分激活值保存下来，其余部分丢弃，这样被丢弃的那一部分激活值需要在计算梯度时重新计算。 下面这个动图展示了一种简单策略：前向传播过程中计算节点的激活值并保存...

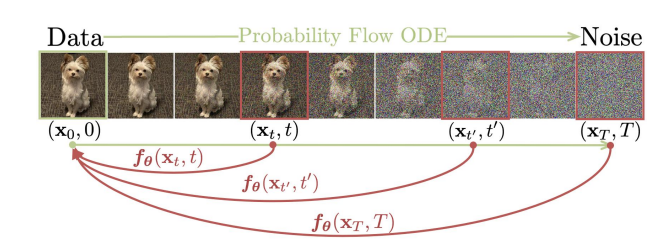
Diffusion Models from SDE 连续扩散模型 (Continuous Diffusion Models) 将传统的离散时间扩散过程扩展到连续时间域,可以被视为一个随机过程，使用随机微分方程(SDE)来描述。其前向过程可以写成如下形式： [公式] 其中， f(x,t) 可以看成偏移系数， g(t) 可以看成是扩散系数， dw 是标准布朗运动。这个SDE 描述了数据在连续时间域内如何被噪声逐渐破坏。 这个随机过程的逆向过程存在（更准确的描述：下面的逆向时间SDE具有与正向过程SDE相同的联合分布）为 [公式] 前面我们得到了扩散过程的逆向过程可以用一个SDE描述(逆向随机过程),事实上，存在一个确定性过程 (用ODE描述)也是它的逆向过程 (更准确的描述：这个ODE过程的在任...

简介 基于lmmsengine中的训练时对数据packing操作以及use_rmpad消除了所有padding计算的逻辑 Packing 总体逻辑基于packing_length 将不同的数据填充到一个sequence中，具体来说 在Datsset中， 如下代码所示，将不同的数据append到buffer列表中 [代码] 在 Collator 组合成batch的形式传入到模型的输入， 这里还是将数据padding [代码] rmpad 项目中，是以 monkey patch的形式（也就是打热补丁） 替换rmpad操作的，如下代码所示，主要就是替换模型中的forward操作 [代码] Qwen3VLModel.forward 显式调用了 _unpad_input。它计算了非 padding 元...

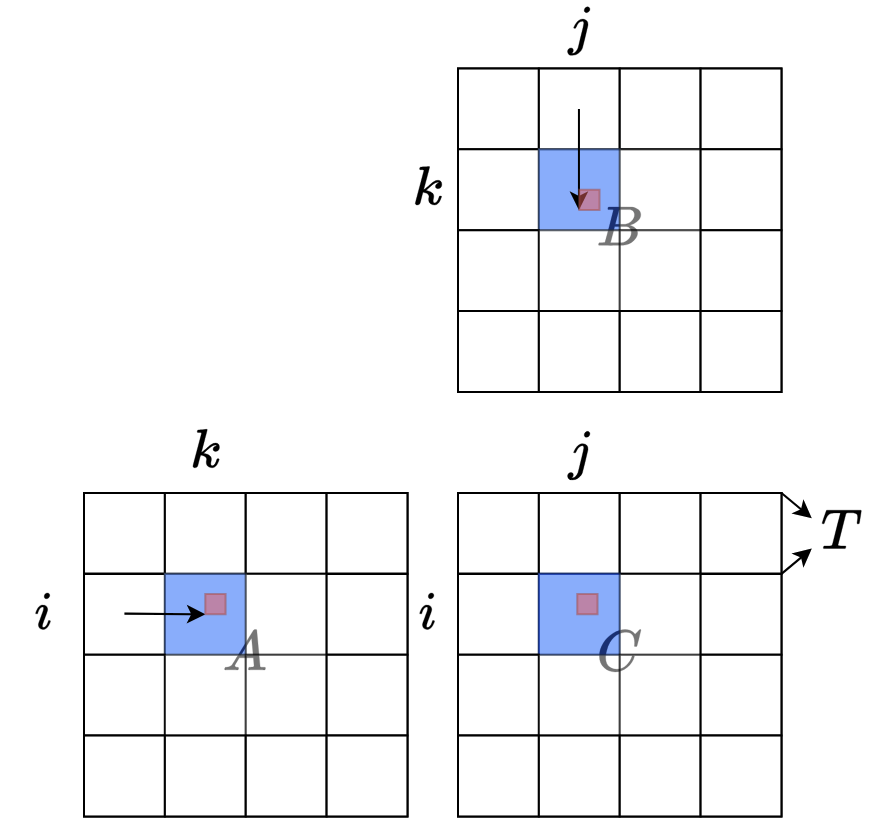
引言与背景 FlashAttention的关键创新在于使用类似于在线Softmax的思想来对自注意力计算进行分块（tiling），从而能够融合整个多头注意力层的计算，而无需访问GPU全局内存来存储中间的logits和注意力分数 在深度学习中，Transformer模型的自注意力机制是计算密集型操作。传统实现需要在GPU全局内存中存储大量中间结果，这导致： 内存瓶颈：中间矩阵占用大量显存 I/O开销：频繁的全局内存访问降低效率 扩展性限制：难以处理超长序列 FlashAttention通过算法创新解决了这些问题。 SelfAtention 自注意力机制的计算可以总结为（为简化说明，忽略头数和批次维度，也省略注意力掩码和缩放因子 [Math] ）： [公式] 其中： Q, K, V, O 都是形...

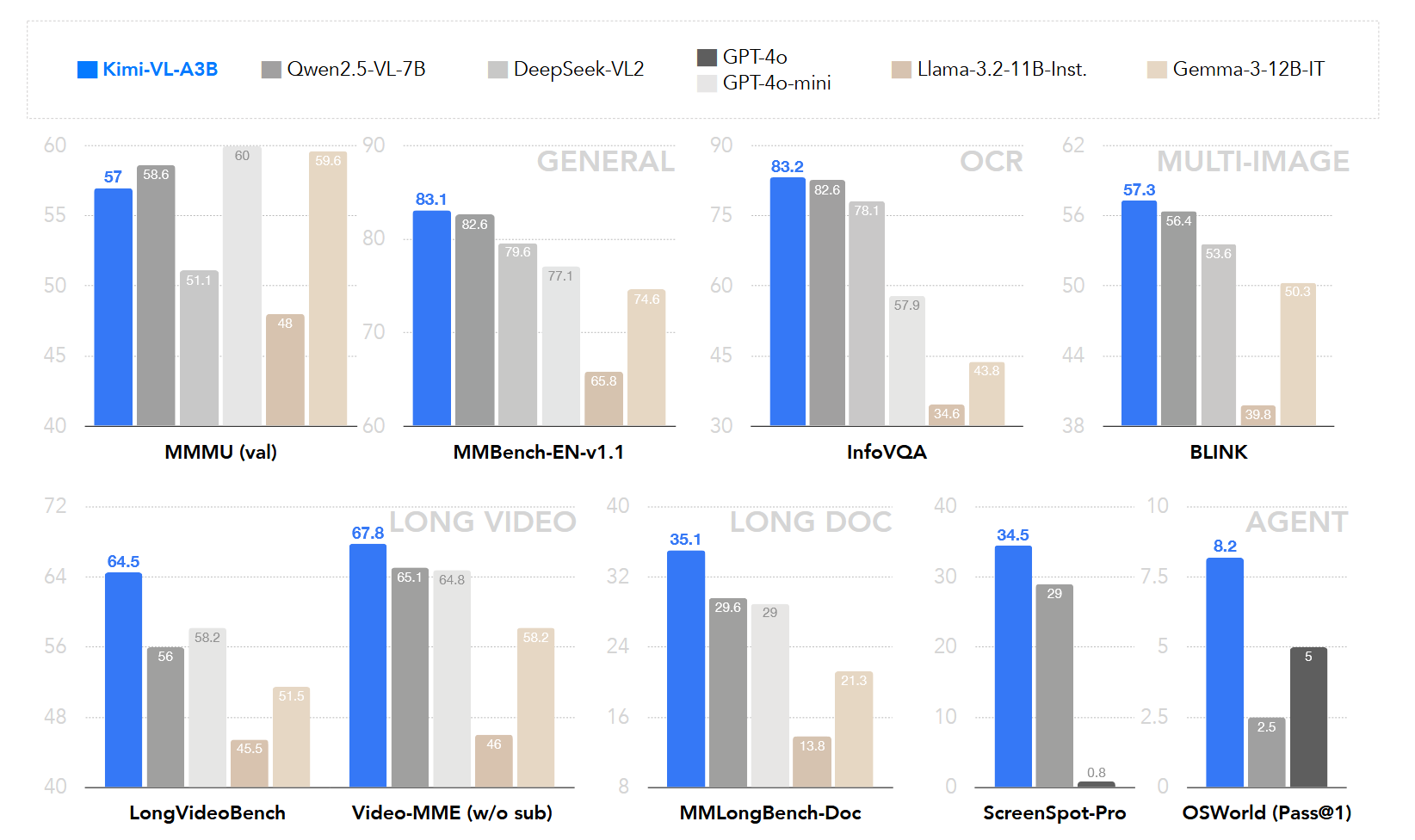
模型概述 KimiVL 是一个高效的开源混合专家视觉语言模型(VLM)，它提供先进的多模态推理、长上下文理解和强大的代理能力，同时在语言解码器中仅激活 2.8B 参数(KimiVLA3B)。该模型在多种挑战性任务中表现出色，包括一般用途的视觉语言理解、多轮代理任务、大学水平的图像和视频理解、OCR、数学推理和多图像理解等. 模型架构 KimiVL 的架构由三个主要部分组成： MoE语言模型 Moonlight MoE language model with only 2.8B activated (16B total) parameters 视觉模型 400M nativeresolution MoonViT vision encoder. MLP Projector MoonViT: 原生...

💡 Score based generative model SMLD的关键点： 正式开始介绍之前首先解答一下这个问题：scorebased 模型是什么东西，微分方程在这个模型里到底有什么用？我们知道生成模型基本都是从某个现有的分布中进行采样得到生成的样本，为此模型需要完成对分布的建模。根据建模方式的不同可以分为隐式建模（例如 GAN、diffusion models）和显式建模（例如 VAE、normalizing flows）。和上述的模型相同，scorebased 模型也是用一定方式对分布进行了建模。具体而言，这类模型建模的对象是概率分布函数 log 的梯度，也就是 score function，而为了对这个建模对象进行学习，需要使用一种叫做 score matching 的技术，这也...

💡 随机微分 在DDPM中，扩散过程被划分为了固定的T步，还是用DDPM中的类比来说，就是“拆楼”和“建楼”都被事先划分为了T步，这个划分有着相当大的人为性。事实上，真实的“拆”、“建”过程应该是没有刻意划分的步骤的，我们可以将它们理解为一个在时间上连续的变换过程，可以用随机微分方程（Stochastic Differential Equation，SDE）来描述。 为此，我们用下述SDE描述前向过程（“拆楼”）： [公式] 相信很多读者都对SDE很陌生，笔者也只是在硕士阶段刚好接触过一段时间，略懂皮毛。不过不懂不要紧，我们只需要将它看成是下述离散形式在 [Math] 时的极限： [公式] 再直白一点，如果假设拆楼需要1天，那么拆楼就是 [Math] 从 t=0 到 t=1 的变化过程，每一...