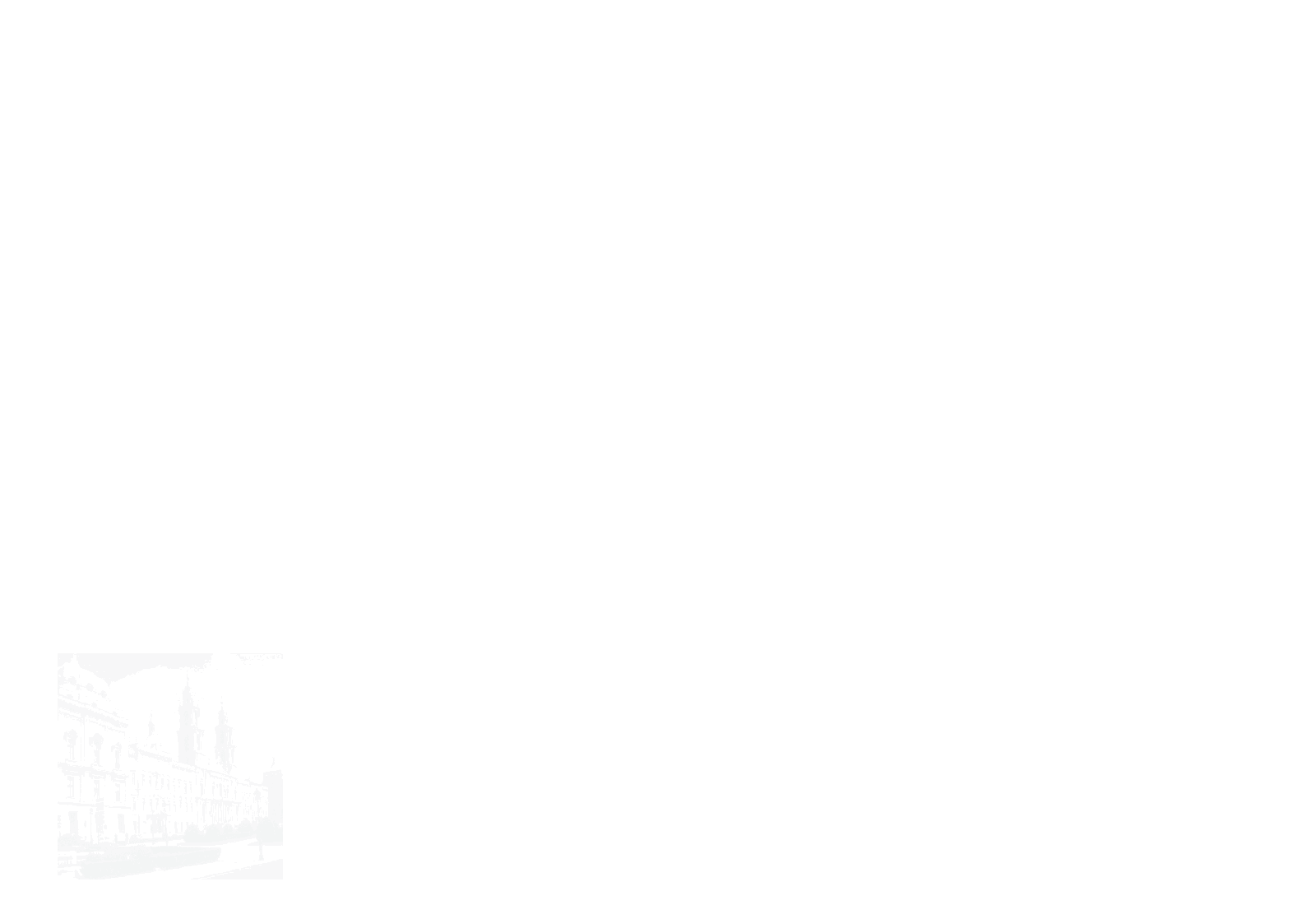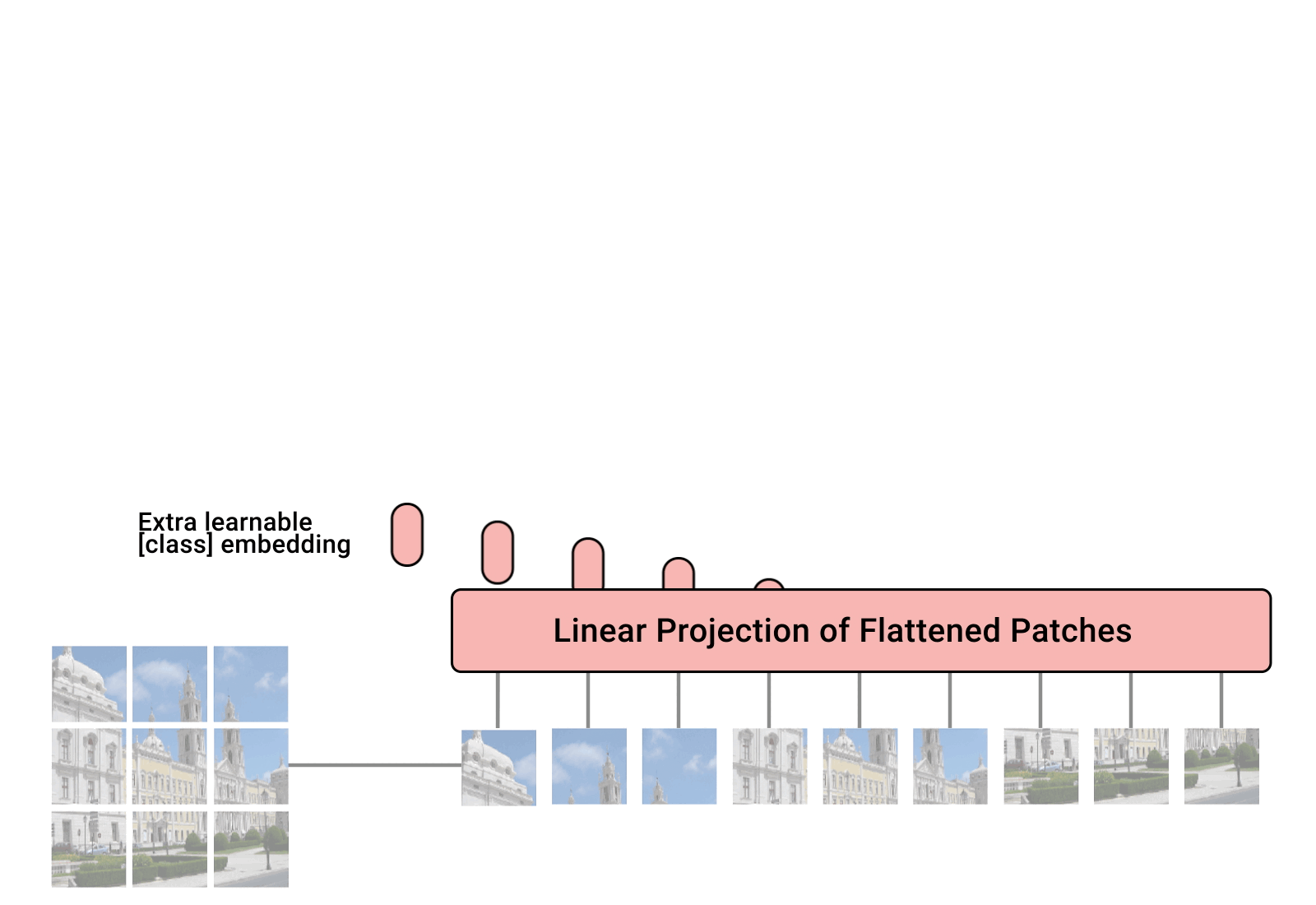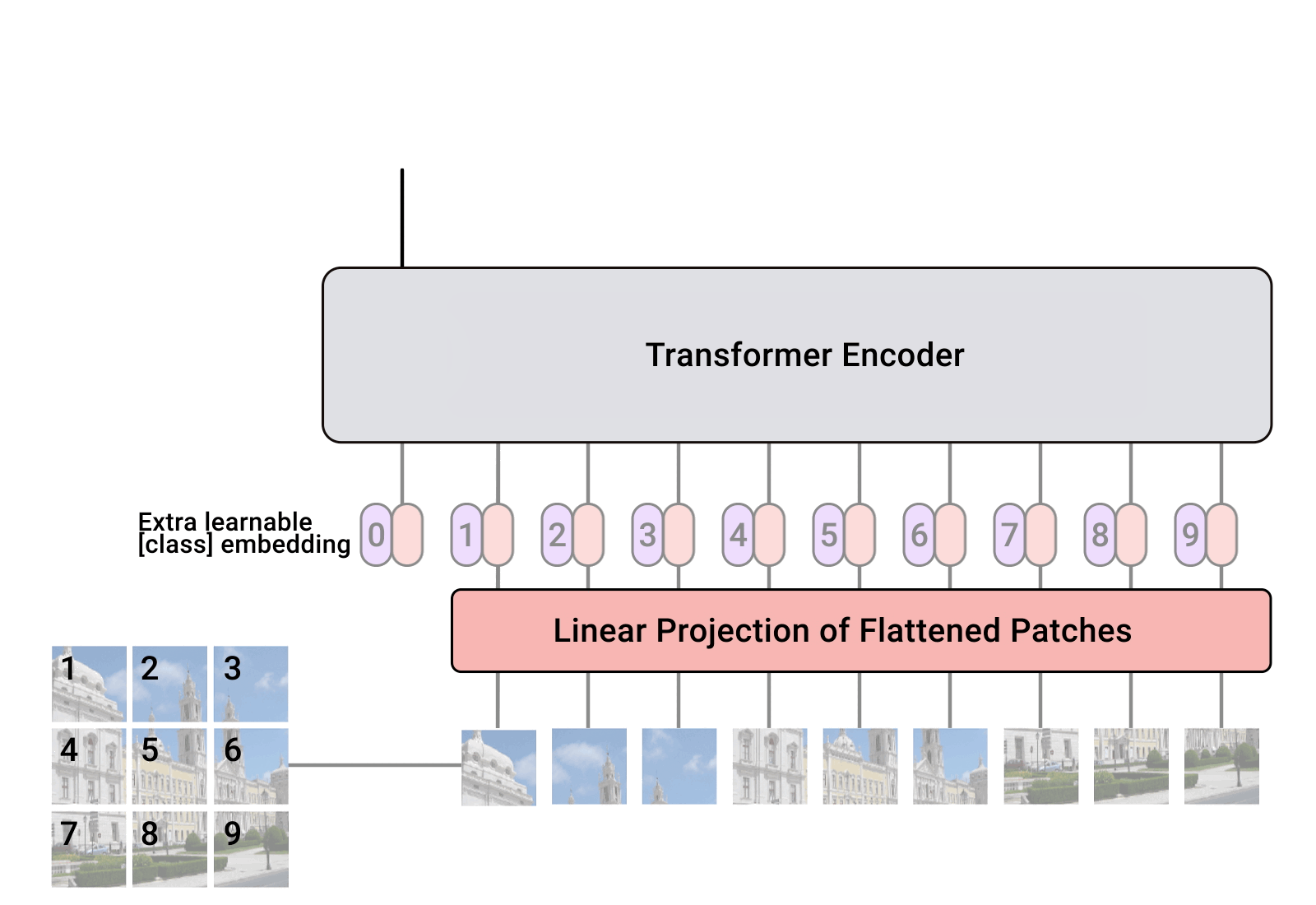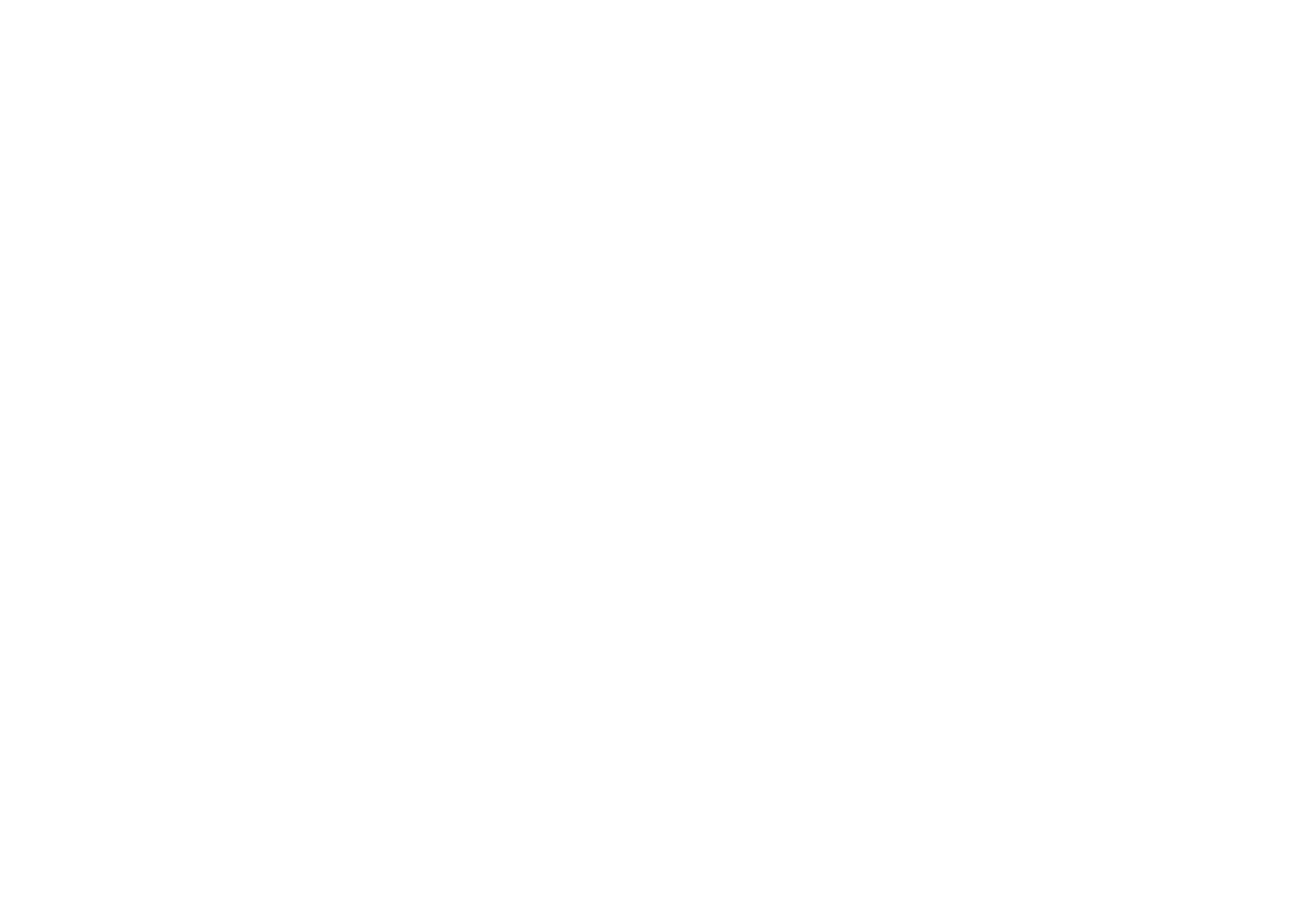INCOMING TRANSMISSION

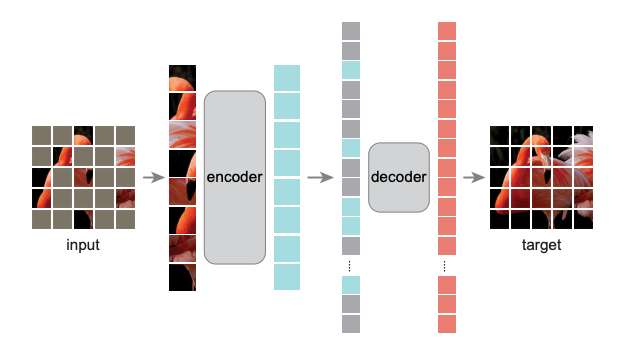
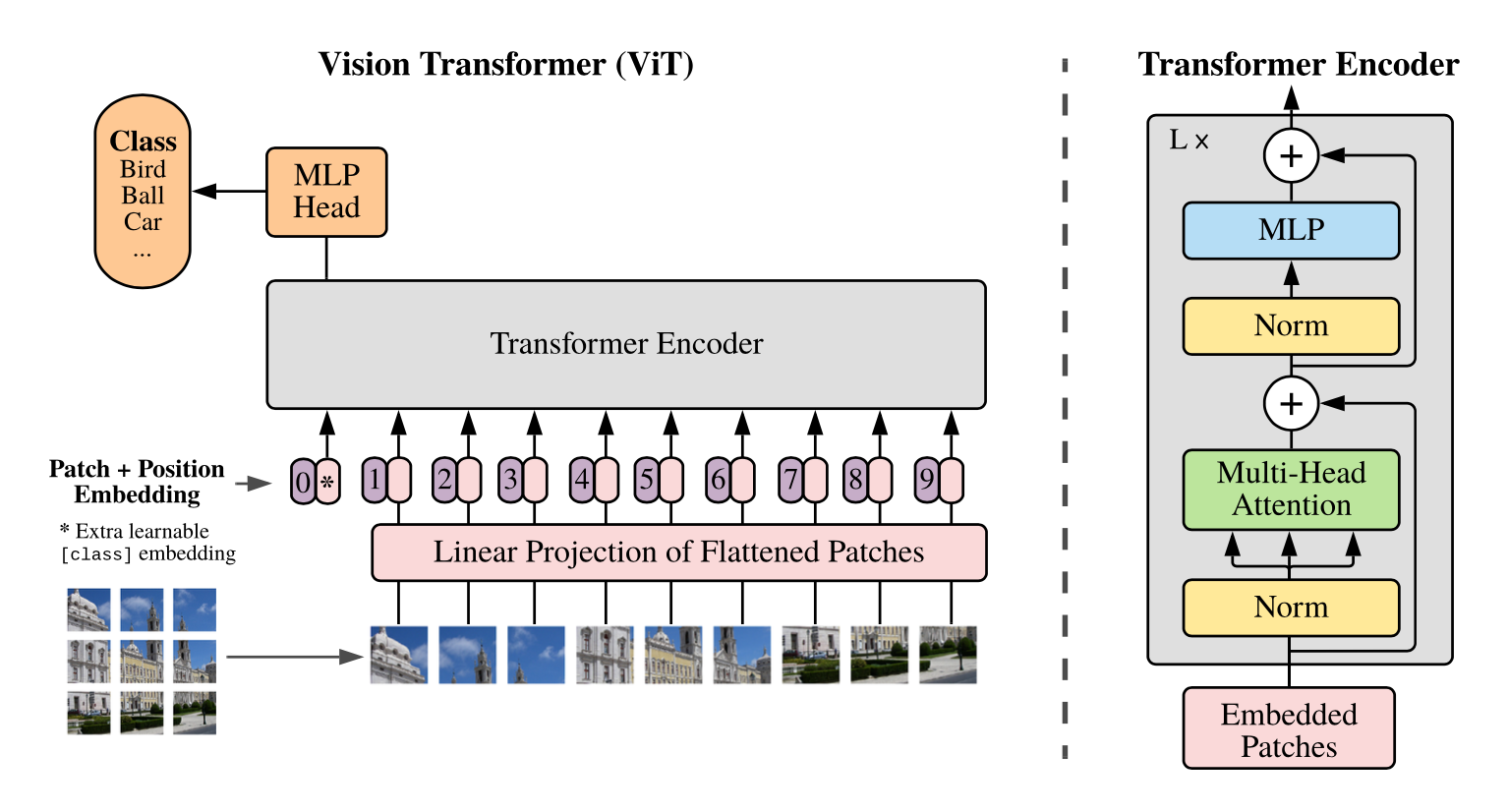
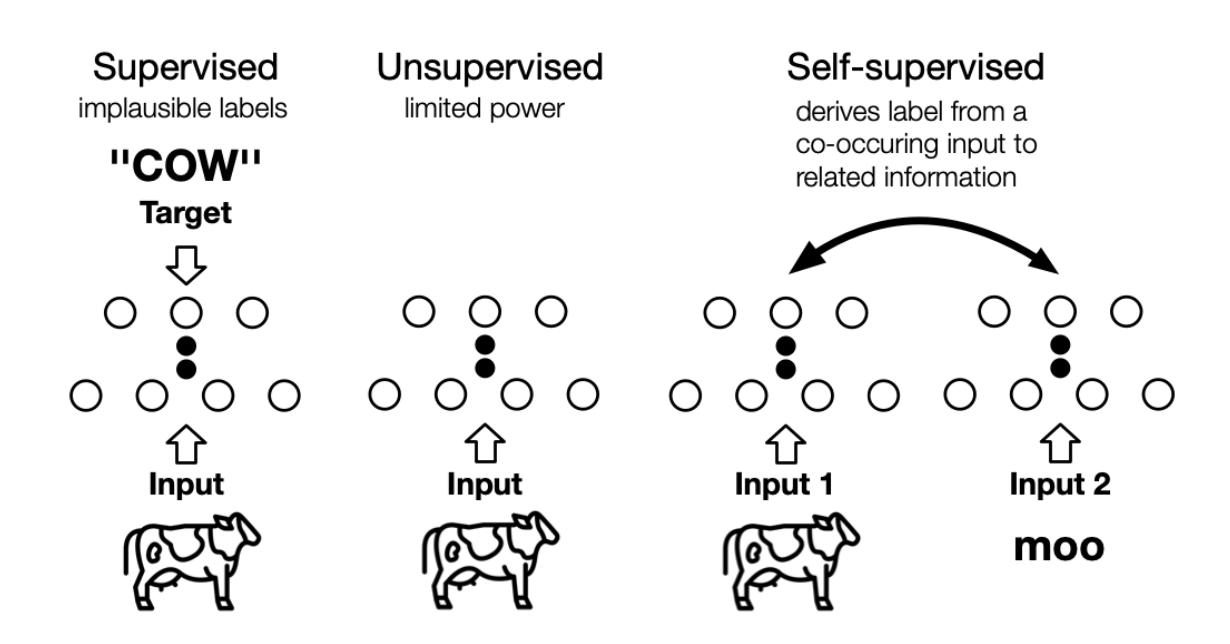
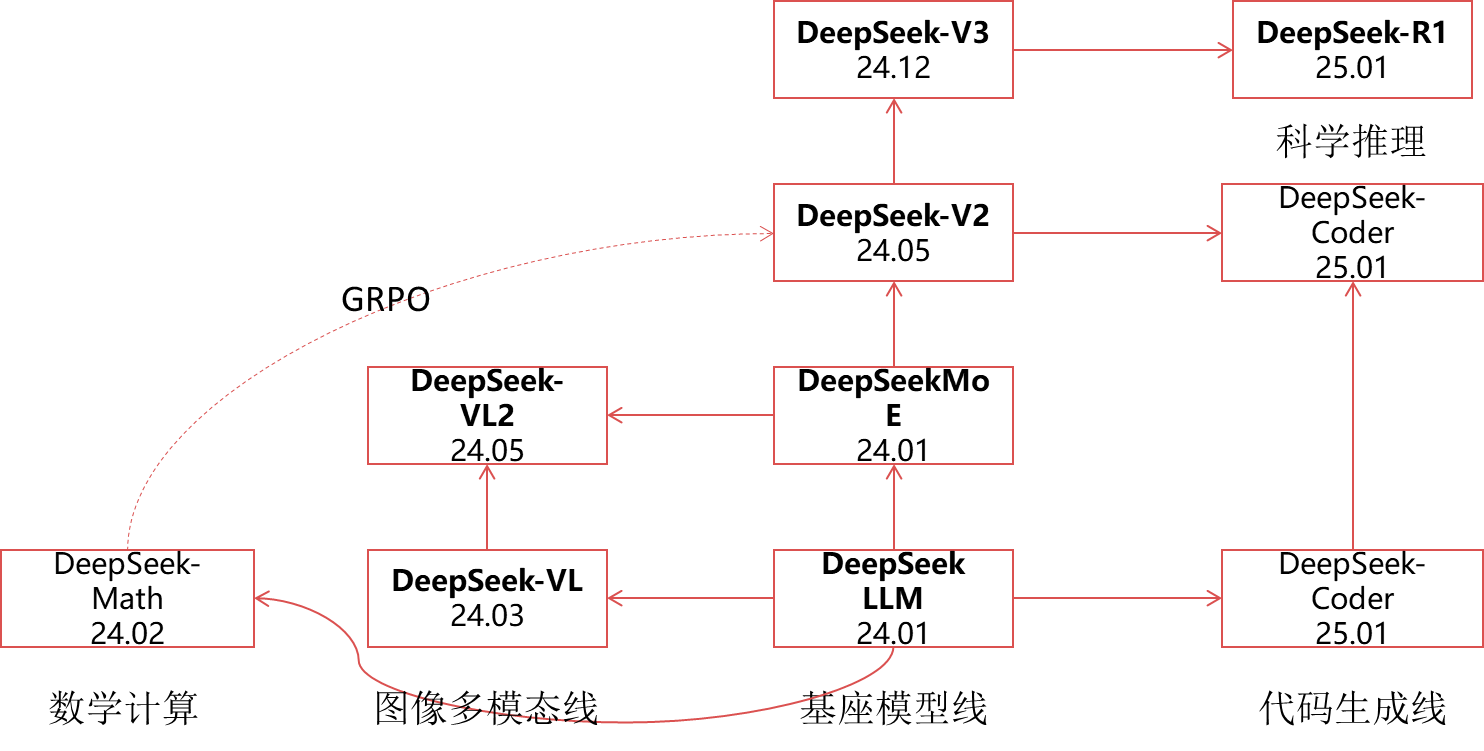
导言 自监督学习（Self-Supervised Learning）能利用大量无标注的数据进行表征学习，然后在特定下游任务上对参数进行微调。通过这样的方式，能够在较少有标注数据上取得优于有监督学习方法的精度。近年来，自监督学习受到了越来越多的关注，如Yann Lecun也在 AAAI 上讲 Self-Supervised Learning 是未来的大势所趋。在CV领域涌现了如SwAV、MOCO、DINO、MoBY等一系列工作。MAE是kaiming继MOCO之后在自监督学习领域的又一力作。首先，本文会对MAE进行解读，然后基于EasyCV库的精度复现过程及其中遇到的一些问题作出解答。 概述 MAE的做法很简单：随机mask掉图片中的一些patch，然后通过模型去重建这些丢失的区域。包括两个核心的设计：1.非对称编码-解码结构 2.用较高的掩码率（75%）。通过这两个设计MAE在预训练过程中可以取得3倍以上的训练速度和更高的精度，如ViT-Huge能够通过ImageNet-1K数据上取得87.8%的准确率。 模型拆解...

概述 在计算机视觉领域（CV），对视觉特征的理解CNN是长期处于主导地位的。而在NLP领域，Transformer框架的巨大成功，也激发了不少研究者探索将Transformer用于计算机视觉任务。ViT（Vision Transformer）的出现标志着在CV领域Transformer架构迈出了重要的一步。尤其在当前结合LLM的多模态探索上（MM-LLM），都是以LLM大语言模型为骨干架构的模型，多种模态的信息需要先做token化处理，再输入到LLM模型。ViT天然具有序列化特征的建模能力，自然在MM-LLM探索中大放异彩~ ViT在多模态模型中的角色类似于自然语言建模中的Tokenizer组件，对图像进行视觉特征编码，产出图像的序列特征。只不过ViT的编码过程本身也是采用了Transformer的模型结构。 本文主要结合几篇paper和源码讲讲ViT和针对ViT的一些优化方法~ ViT（Vision Transformer）...

ViT（vision transformer）是Google在2020年提出的直接将transformer应用在图像分类的模型，后面很多的工作都是基于ViT进行改进的。ViT的思路很简单：直接把图像分成固定大小的patchs，然后通过线性变换得到patch embedding，这就类比NLP的words和word embedding，由于transformer的输入就是a sequence of token embeddings，所以将图像的patch embeddings送入transformer后就能够进行特征提取从而分类了。ViT模型原理如下图所示，其实ViT模型只是用了transformer的Encoder来提取特征（原始的transformer还有decoder部分，用于实现sequence to sequence，比如机器翻译）。下面将分别对各个部分做详细的介绍。 Patch Embedding 对于ViT来说，首先要将原始的2-D图像转换成一系列1-D的patch embeddings，这就好似NLP中的word embedding。输入的2-D图像记为 \(x\in...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...

研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

🔖 https://www.deepseek.com/ DeepSeek LLM 代码地址： https://github.com/deepseek-ai/DeepSeek-LLM 背景 量化巨头幻方探索AGI（通用人工智能）新组织“深度求索”在成立半年后，发布的第一代大模型，免费商用，完全开源。作为一家隐形的AI巨头，幻方拥有1万枚英伟达A100芯片，有手撸的HAI-LLM训练框架HAI-LLM：高效且轻量的大模型训练工具。 概述 DeepSeek LLMs，这是一系列在2万亿标记的英语和中文大型数据集上从头开始训练的开源模型 在本文中，深入解释了超参数选择、Scaling Laws以及做过的各种微调尝试。校准了先前工作中的Scaling Laws，并提出了新的最优模型/数据扩展-缩放分配策略。此外，还提出了一种方法，使用给定的计算预算来预测近似的batch-size和learning-rate。进一步得出结论，Scaling Laws与数据质量有关，这可能是不同工作中不同扩展行为的原因。在Scaling Laws的指导下，使用最佳超参数进行预训练，并进行全面评估。...

简介 24年12月,研究团队开发了 DeepSeek-V3，这是一个基于 MoE 架构的大模型，总参数量达到 671B，其中每个 token 会激活 37B 个参数。 基于提升性能和降低成本的双重目标，在架构设计方面，DeepSeek-V3 采用了 MLA 来确保推理效率，并使用 DeepSeekMoE 来实现经济高效的训练。这两种架构在 DeepSeek-V2 中已经得到验证，证实了它们能够在保持模型性能的同时实现高效的训练和推理。 除了延续这些基础架构外，研究团队还引入了两项创新策略来进一步提升模型性能。 首先，DeepSeek-V3 首创了 无辅助损失的负载均衡 策略(auxiliary-loss-free strategy for load balancing)，有效降低了负载均衡对模型性能的负面影响。另外，DeepSeek-V3 采用了 多 token 预测训练目标， 这种方法在评估基准测试中展现出了显著的性能提升。 为了提高训练效率，该研究采用了 FP8 混合精度训练技术...

简介 生成树（spanning tree） 在图论中，无向图 G=(V,E) 的生成树（spanning tree)是具有G的全部顶点，但边数最少的联通子图。假设G中一共有n个顶点，一颗生成树满足下列条件： （1）n个顶点； （2）n1条边； （3）n个顶点联通； （4）一个图的生成树可能有多个。最小生成树（minimum spanning tree， MST）/最小生成森林：联通加权无向图中边缘权重加和最小的生成树。给定无向图 G=(V,E) ， (u,v) 代表顶点 u 与顶点 v 的边， w(u,v) 代表此边的权重，若存在生成树T使得： [公式] 最小，则 T 为 G 的最小生成树。对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。最小生成树除了继承...

给一个无向图，判断其是否为一棵树。如果是树的话，所有的节点必须是连接的，也就是说必须是连通图，而且不能有环，所以就变成了验证是否是连通图和是否含有环。 [代码]

题目 中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。 例如， [2,3,4] 的中位数是 3 [2,3] 的中位数是 (2 + 3) / 2 = 2.5 设计一个支持以下两种操作的数据结构： void addNum(int num) 从数据流中添加一个整数到数据结构中。 double findMedian() 返回目前所有元素的中位数。 示例： addNum(1) addNum(2) findMedian() 1.5 addNum(3) findMedian() 2 题解 维护两个堆：大顶堆和小顶堆。并且需满足如下条件： 小顶堆的所有元素都大于等于大顶堆的所有元素。 大顶堆中的元素数量大于等于小顶堆中的元素数量。 大顶堆对应排序后的列表的左半部分；小顶堆对应排序...

[代码] 自己实现小顶堆 [代码] 变态的需求来了：给出N长的序列，求出BtmK小的元素，即使用大顶堆。 概括一种最简单的： 将push(e)改为push(e)、pop(e)改为pop(e)。 也就是说，在存入堆、从堆中取出的时候，都用相反数，而其他逻辑与TopK完全相同，看代码： [代码] 自己实现大顶堆 [代码]