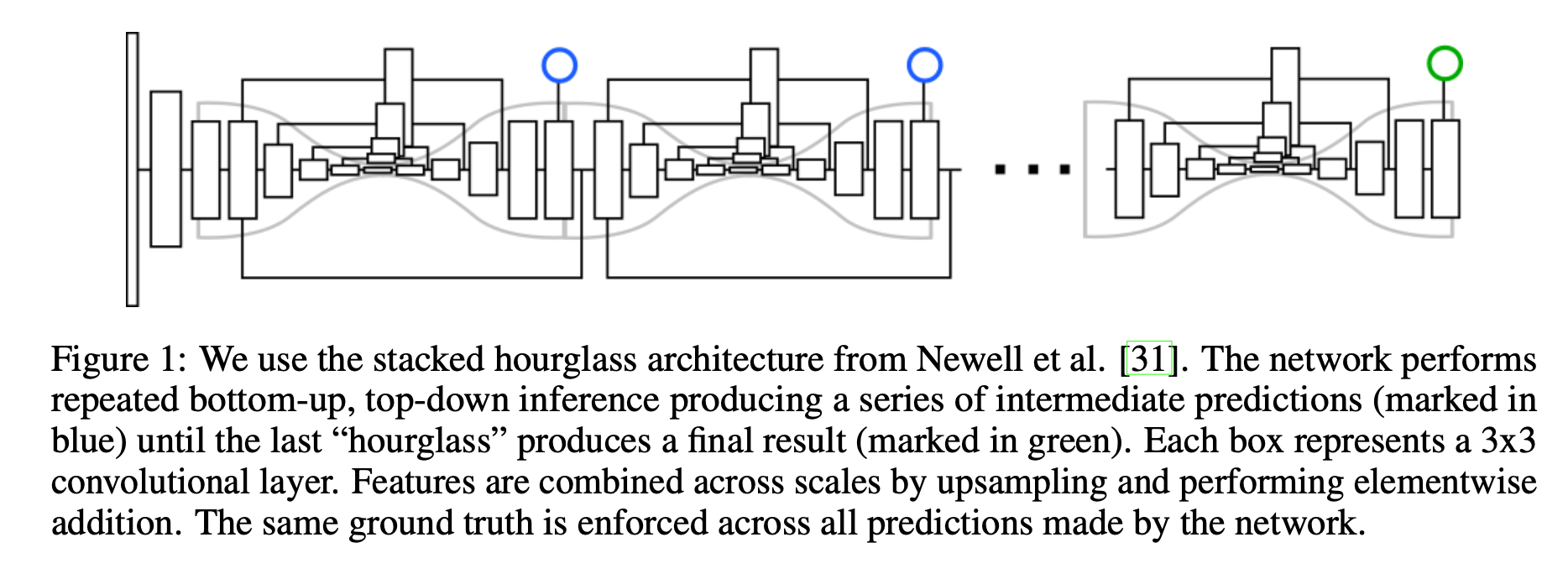
Deep Learning
2026-01-11
一般来说,神经网络处理的东西都是连续的浮点数,标准的输出也是连续型的数字。但实际问题中,我们很多时候都需要一个离散的结果,比如分类问题中我们希望输出正确的类别,“类别”是离散的,“类别的概率”才是连续的;又比如我们很多任务的评测指标实际上都是离散的,比如分类问题的正确率和F1、机器翻译中的BLEU,等等。 还是以分类问题为例,常见的评测指标是正确率,而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联,但它们不是绝对的单调相关关系。换句话说,交叉熵下降了,正确率不一定上升。显然,如果能用正确率的相反数做损失函数,那是最理想的,但正确率是不可导的(涉及到 [Math] 等操作),所以没法直接用。 这时候一般有两种解决方案;一是动用强化学习,将正确率设为奖励函数,这是“用牛刀杀...