INCOMING TRANSMISSION

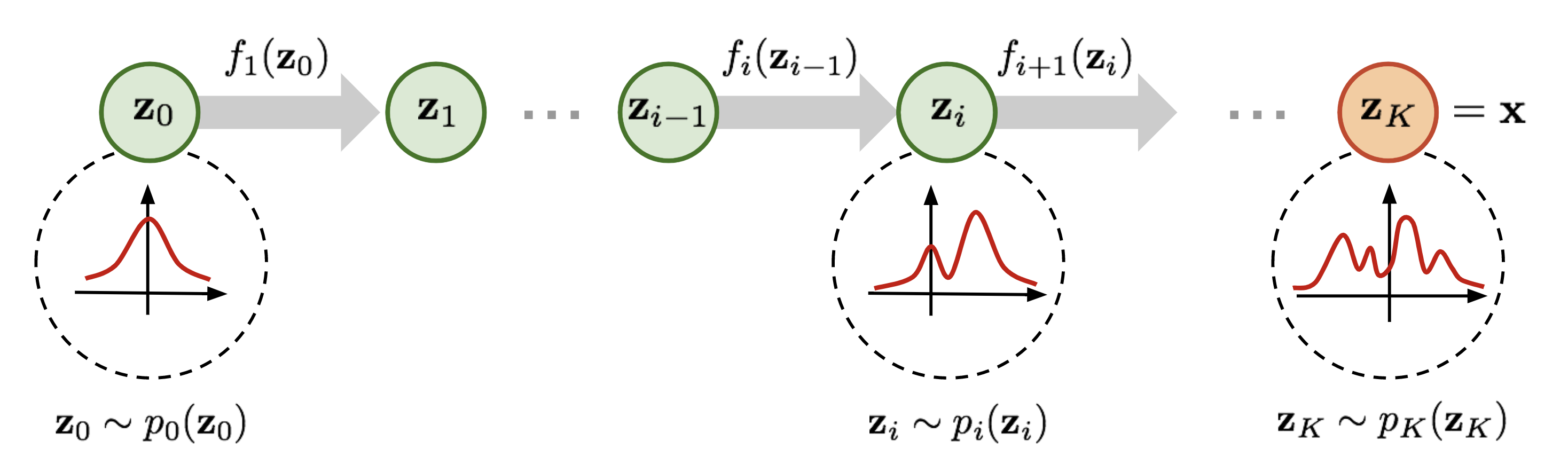
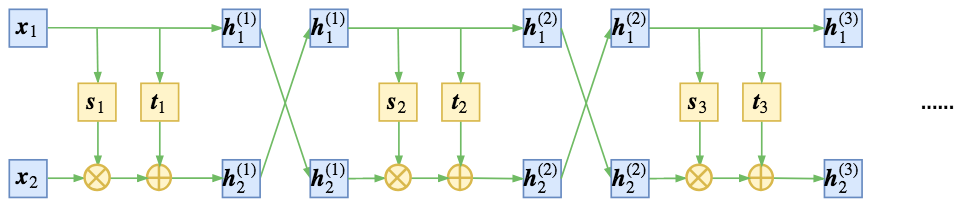
Normalizing flow（标准化流）是一类对概率分布进行建模的工具，它能完成简单的概率分布（例如高斯分布）和任意复杂分布之间的相互转换，经常被用于 data generation、density estimation、inpainting 等任务中，例如 Stability AI 提出的 Stable Diffusion 3 中用到的 rectified flow 就是 normalizing flow 的变体之一。 为了便于理解，在正式开始介绍之前先简要说明一下 normalizing flow 的做法。如上图所示，为了将一个高斯分布 \(z_0\) 转换为一个复杂的分布 \(z_K\) ，normalizing flow 会对初始的分布 \(z_0\) 进行多次可逆的变换，将其逐渐转换为 \(z_K\) 。由于每一次变换都是可逆的，从 \(z_K\) 出发也能得到高斯分布 \(z_0\) 。这样，我们就实现了复杂分布与高斯分布之间的互相转换，从而能从简单的高斯分布建立任意复杂分布。 对 diffusion models 比较熟悉的读者可能已经发现了，这个过程和...

分布变换 通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量 \(Z\) 生成目标数据 \(X\) 的模型，但是实现上有所不同。更准确地讲，它们是假设了 \(Z\) 服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型 \(X=g(Z)\) ，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。 生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式 那现在假设 \(Z\) 服从标准的正态分布，那么我就可以从中采样得到若干个 \(Z_1, Z_2, \dots, Z_n\) ，然后对它做变换得到 \(\hat{X}_1 = g(Z_1),\hat{X}_2 = g(Z_2),\dots,\hat{X}_n = g(Z_n)\) ，我们怎么判断这个通过 \(g\)...

研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

相关内容 自监督学习（Selfsupervised）：属于无监督学习，其核心是自动为数据打标签（伪标签或其他角度的可信标签，包括图像的旋转、分块等等），通过让网络按照既定的规则，对数据打出正确的标签来更好地进行特征表示，从而应用于各种下游任务。 互信息（Mutual Information）：表示两个变量 X 和 Y 之间的关系，定义为： 噪声对抗估计（Noise Contrastive Estimation, NCE）：在NLP任务中一种降低计算复杂度的方法，将语言模型估计问题简化为一个二分类问题。 Introduction 无监督学习一个重要的问题就是学习有用的 representation，本文的目的就是训练一个 representation learning 函数（即编码器encod...

背景 本文主要是《NICE: Nonlinear Independent Components Estimation》一文的介绍和实现。这篇文章也是glow这个模型的基础文章之一，可以说它就是glow的奠基石。 艰难的分布 众所周知，目前主流的生成模型包括VAE和GAN，但事实上除了这两个之外，还有基于flow的模型（flow可以直接翻译为“流”，它的概念我们后面再介绍）。事实上flow的历史和VAE、GAN它们一样悠久，但是flow却鲜为人知。在我看来，大概原因是flow找不到像GAN一样的诸如“造假者鉴别者”的直观解释吧，因为flow整体偏数学化，加上早期效果没有特别好但计算量又特别大，所以很难让人提起兴趣来。不过现在看来，OpenAI的这个好得让人惊叹的、基于flow的glow模型，估...

💡 原本随机采样的DDPM模型中，也隐含了一个确定性的采样过程DDIM，它的连续极限也是一个ODE。 细想上述过程，可以发现不管是“DDPM→DDIM”还是“SDE→ODE”，都是从随机采样模型过渡到确定性模型，而如果我们一开始的目标就是ODE，那么该过程未免显得有点“迂回”了。在本文中，笔者尝试给出ODE扩散模型的直接推导，并揭示了它与雅可比行列式、热传导方程等内容的联系。 Rectified Flow 理论推导 微分方程 像GAN这样的生成模型，它本质上是希望找到一个确定性变换，能将从简单分布（如标准正态分布）采样出来的随机变量，变换为特定数据分布的样本。flow模型也是生成模型之一，它的思路是反过来，先找到一个能将数据分布变换简单分布的可逆变换，再求解相应的逆变换来得到一个生成模型。 ...

DDPM 有一个非常明显的问题：采样过程很慢。因为 DDPM 的反向过程利用了马尔可夫假设，所以每次都必须在相邻的时间步之间进行去噪，而不能跳过中间步骤。原始论文使用了 1000 个时间步，所以我们在采样时也需要循环 1000 次去噪过程，这个过程是非常慢的。 为了加速 DDPM 的采样过程，DDIM 在不利用马尔可夫假设的情况下推导出了 diffusion 的反向过程，最终可以实现仅采样 20～100 步的情况下达到和 DDPM 采样 1000 步相近的生成效果，也就是提速 10～50 倍。这篇文章将对 DDIM 的理论进行讲解，并实现 DDIM 采样的代码。 DDPM 的反向过程 首先我们回顾一下 DDPM 反向过程的推导，为了推导出 [Math] 这个条件概率分布，DDPM 利用贝叶斯...

PrefixTuning Paper: 2021.1 Optimizing Continuous Prompts for GenerationGithub：https://github.com/XiangLi1999/PrefixTuningPrompt: Continus Prefix PromptTask & Model：BART(Summarization), GPT2(Table2Text) 最早提出Prompt微调的论文之一，其实是可控文本生成领域的延伸，因此只针对摘要和Table2Text这两个生成任务进行了评估。 PrefixTuning可以理解是CTRL模型的连续化升级版，为了生成不同领域和话题的文本，CTRL是在预训练阶段在输入文本前加入了control code，例如好评...

背景 随着预训练语言模型进入LLM时代，其参数量愈发庞大。全量微调模型所有参数所需的显存早已水涨船高。 例如： 全参微调Qwen1.57BChat预估要2张80GB的A800，160GB显存 全参微调Qwen1.572BChat预估要20张80GB的A800，至少1600GB显存。 而且，通常不同的下游任务还需要LLM的全量参数，对于算法服务部署来说简直是个灾难 当然，一种折衷做法就是全量微调后把增量参数进行SVD分解保存，推理时再合并参数 为了寻求一个不更新全部参数的廉价微调方案，之前一些预训练语言模型的高效微调(Parameter Efficient finetuning, PEFT)工作，要么插入一些参数或学习外部模块来适应新的下游任务。 Adapter tuning Adapter ...

Diffusion Models from SDE 连续扩散模型 (Continuous Diffusion Models) 将传统的离散时间扩散过程扩展到连续时间域,可以被视为一个随机过程，使用随机微分方程(SDE)来描述。其前向过程可以写成如下形式： [公式] 其中， f(x,t) 可以看成偏移系数， g(t) 可以看成是扩散系数， dw 是标准布朗运动。这个SDE 描述了数据在连续时间域内如何被噪声逐渐破坏。 这个随机过程的逆向过程存在（更准确的描述：下面的逆向时间SDE具有与正向过程SDE相同的联合分布）为 [公式] 前面我们得到了扩散过程的逆向过程可以用一个SDE描述(逆向随机过程),事实上，存在一个确定性过程 (用ODE描述)也是它的逆向过程 (更准确的描述：这个ODE过程的在任...

精巧的flow 不得不说，flow模型是一个在设计上非常精巧的模型。总的来看，flow就是想办法得到一个encoder将输入 𝑥 编码为隐变量 𝑧，并且使得 𝑧 服从标准正态分布。得益于flow模型的精巧设计，这个encoder是可逆的，从而我们可以立马从encoder写出相应的decoder（生成器）出来，因此，只要encoder训练完成，我们就能同时得到decoder，完成生成模型的构建。 为了完成这个构思，不仅仅要使得模型可逆，还要使得对应的雅可比行列式容易计算，为此，NICE提出了加性耦合层，通过多个加性耦合层的堆叠，使得模型既具有强大的拟合能力，又具有单位雅可比行列式。就这样，一种不同于VAE和GAN的生成模型——flow模型就这样出来了，它通过巧妙的构造，让我们能直接去拟合概率分...

💡 Flowbased Models Normalizing Flow Normalizing Flow 是一种基于变换对概率分布进行建模的模型，其通过一系列离散且可逆的变换实现任意分布与先验分布（例如标准高斯分布）之间的相互转换。在 Normalizing Flow 训练完成后，就可以直接从高斯分布中进行采样，并通过逆变换得到原始分布中的样本，实现生成的过程。（有关 Normalizing Flow 的详细理论） 从这个角度看，Normalizing Flow 和 Diffusion Model 是有一些相通的，其做法的对比如下表所示。从表中可以看到，两者大致的过程是非常类似的，尽管依然有些地方不一样，但这两者应该可以通过一定的方法得到一个比较统一的表示。 Continuous Norma...