INCOMING TRANSMISSION

补充知识 表示学习 （Representation Learning）： 学习数据的表征，以便在构建分类器或其他预测器时更容易提取有用的信息 ，无监督学习也属于表示学习。 互信息 （Mutual Information）：表示两个变量 \(X\) 和 \(Y\) 之间的关系，定义为： \[I(X;Y)=\sum_{x\in X}\sum_{y\in Y}p(x,y)log\frac{p(x|y)}{p(x)}\] 对比损失(contrastive loss) ：计算成对样本的匹配程度，主要用于降维中。计算公式为： \[L=\frac{1}{2N}\sum_{n-1}^N[yd^2+(1-y)max(margin-d, 0)^2]\] 其中, \(d=\sqrt{(a_n-b_n)^2}\) 为两个样本的欧式距离， \(y=\{0,1\}\) 代表两个样本的匹配程度， \(margin\) 代表设定的阈值。这种损失函数可以很好的表达成对样本的匹配程度，也能够很好用于训练提取特征的模型。当 \( y=1\) （即样本相似）时，损失函数只剩下 \(∑d^2\)...

从 NLP 入手 n-gram 语言模型（language model）就是假设一门语言所有可能的句子服从一个概率分布，每个句子出现的概率加起来是1，那么语言模型的任务就是预测每个句子在语言中出现的概率。如果把句子 \(s\) 看成单词 \(w\) 的序列 \(s=\{w_1,w_2,...,w_m\}\) ，那么语言模型就是建模一个 \(p(w_1,w_2,...,w_m)\) 来计算这个句子 \(s\) 出现的概率，直观上我们要得到这个语言模型，基于链式法则可以表示为每个单词出现的条件概率的乘积，我们将条件概率的条件 \((w_1,w_2,...,w_{i-1})\) 称为单词 \(w_i\) 的上下文，用 \(c_i\) 表示。 \[\begin{aligned} p\left(w_{1}, w_{2}, \ldots, w_{m}\right)&=p\left(w_{1}\right) * p\left(w_{2} \mid w_{1}\right) * p\left(w_{3} \mid w_{1}, w_{2}\right) \ldots p\left(w_{m}...

文章从连续情形出发开始介绍重参数，主要的例子是正态分布的重参数；然后引入离散分布的重参数，这就涉及到了Gumbel Softmax，包括Gumbel Softmax的一些证明和讨论；最后再讲讲重参数背后的一些故事，这主要跟梯度估计有关。 基本概念 重参数（Reparameterization） 实际上是处理如下期望形式的目标函数的一种技巧： \[L_{\theta}=\mathbb{E}_{z\sim p_{\theta}(z)}[f(z)]\tag{1}\] 这样的目标在VAE中会出现，在文本GAN也会出现，在强化学习中也会出现（ \(f(z)\) 对应于奖励函数），所以深究下去，我们会经常碰到这样的目标函数。取决于 \(z\) 的连续性，它对应不同的形式： \[\int p_{\theta}(z) f(z)dz\,\,\,\text{(连续情形)}\qquad\qquad \sum_{z} p_{\theta}(z) f(z)\,\,\,\text{(离散情形)}\tag{2}\] 当然，离散情况下我们更喜欢将记号 \(z\) 换成 \(y\) 或者 \(c\) 。 为了最小化...

简介 如果以概率的视角看待世界的生成模型。 在这样的世界观中，我们可以将任何类型的观察数据（例如 \(D\) ）视为来自底层分布（例如 \( p_{data}\) ）的有限样本集。 任何生成模型的目标都是在访问数据集 \(D\) 的情况下近似该数据分布。 如果我们能够学习到一个好的生成模型，我们可以将学习到的模型用于下游推理。 我们主要对数据分布的参数近似感兴趣，在一组有限的参数中，它总结了关于数据集 \(D\) 的所有信息。 与非参数模型相比，参数模型在处理大型数据集时能够更有效地扩展，但受限于可以表示的分布族。 在参数的设置中，我们可以将学习生成模型的任务视为在模型分布族中挑选参数，以最小化模型分布和数据分布之间的距离。 如上图，给定一个狗的图像数据集，我们的目标是学习模型族 \(M\) 中生成模型 θ 的参数，使得模型分布 \(p_θ\) 接近 \(p_{data}\) 上的数据分布。 在数学上，我们可以将我们的目标指定为以下优化问题: \[\mathop{min}\limits_{\theta\in M}d(p_\theta,p_{data})\] 其中， \(d()\)...

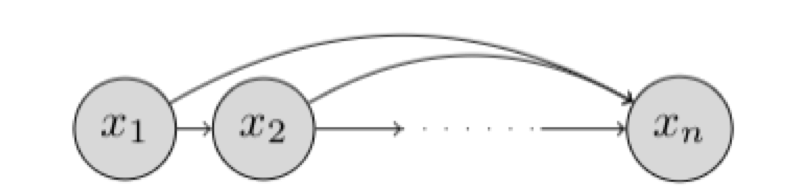
研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

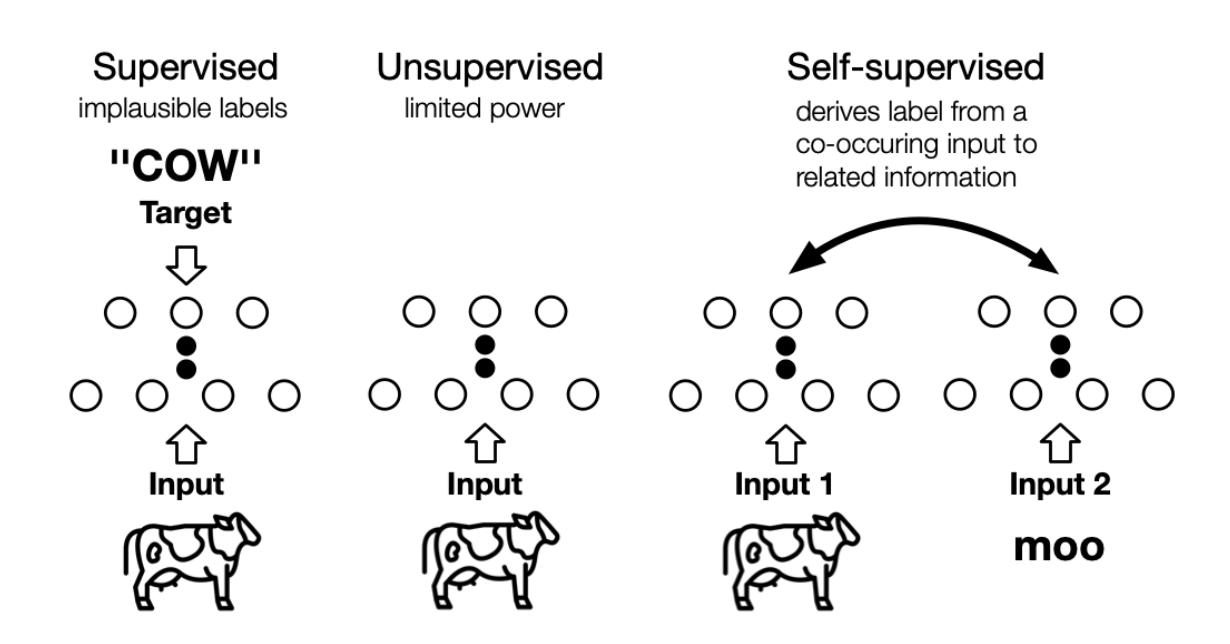
the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

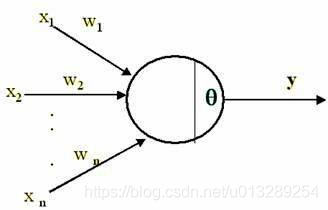
1.深度学习偏置的作用？ 我们在学深度学习的时候，最早接触到的神经网络应该属于感知器（感知器本身就是一个很简单的神经网络，也许有人认为它不属于神经网络，当然认为它和神经网络长得像也行） 要想激活这个感知器，使得 y=1 ，就必须使 x_1w_1 + x_2w_2 +....+x_nw_n T （ T 为一个阈值），而 T 越大，想激活这个感知器的难度越大，人工选择一个阈值并不是一个好的方法，因为样本那么多，我不可能手动选择一个阈值，使得模型整体表现最佳，那么我们可以使得T变成可学习的，这样一来， T 会自动学习到一个数，使得模型的整体表现最佳。当把T移动到左边，它就成了偏置， x_1w_1 + x_2w_2 +....+x_nw_n T 0 xw +b 0 ，总之，偏置的大小控制着激活这个感...

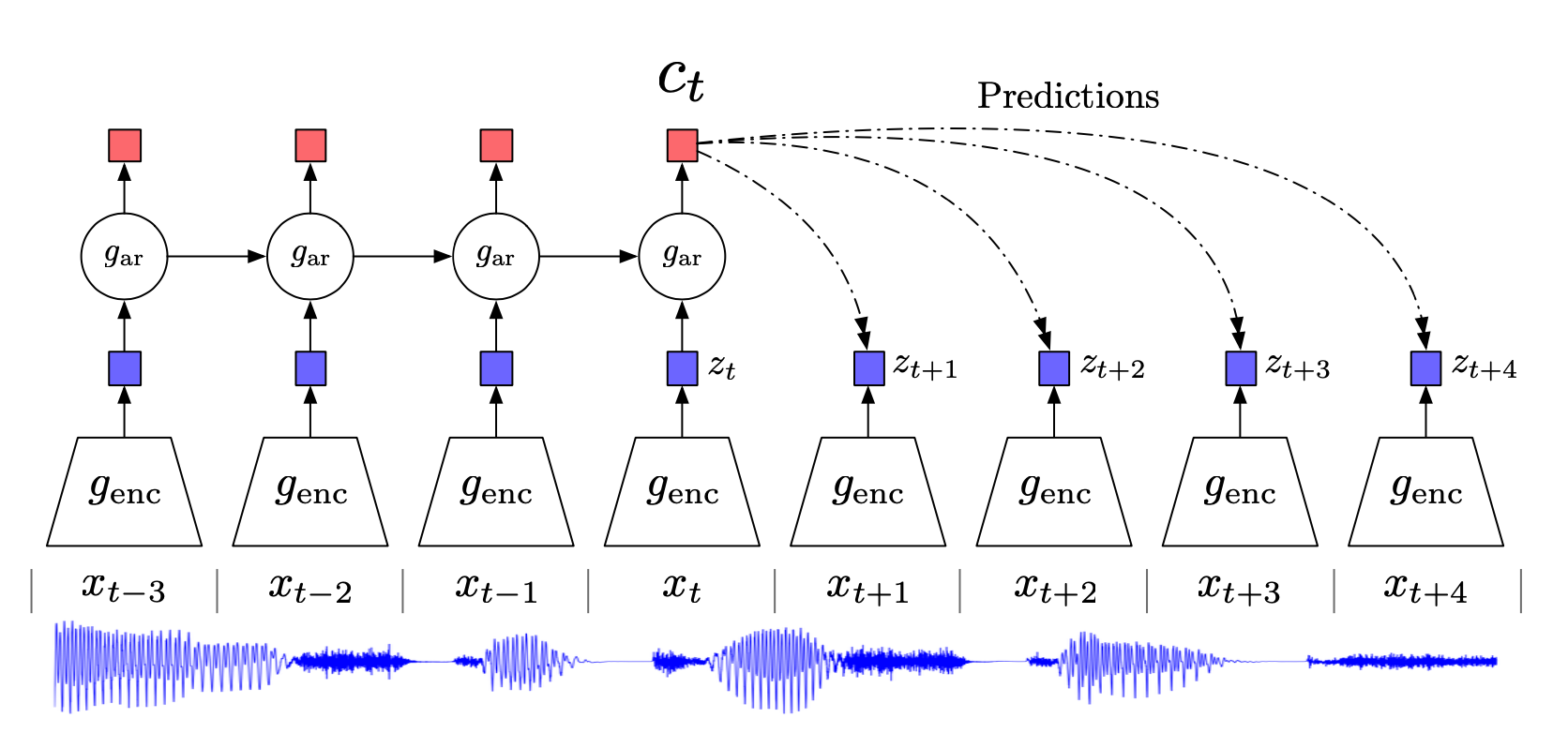
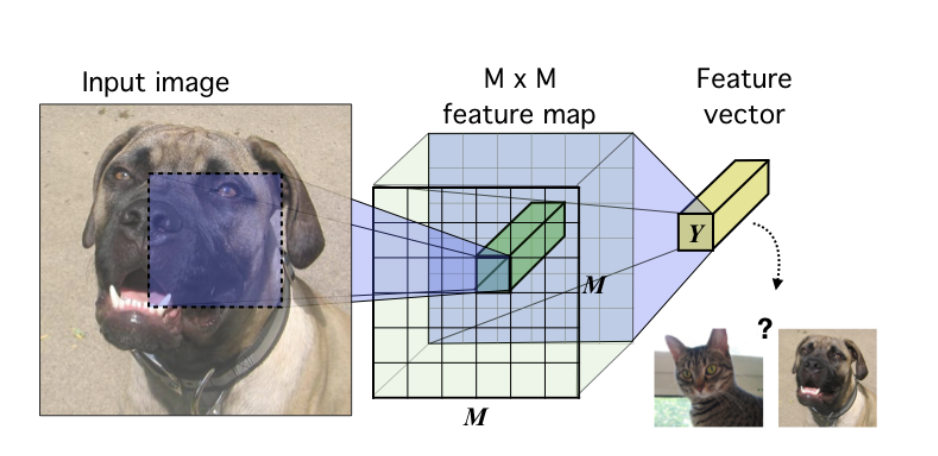
相关内容 自监督学习（Selfsupervised）：属于无监督学习，其核心是自动为数据打标签（伪标签或其他角度的可信标签，包括图像的旋转、分块等等），通过让网络按照既定的规则，对数据打出正确的标签来更好地进行特征表示，从而应用于各种下游任务。 互信息（Mutual Information）：表示两个变量 X 和 Y 之间的关系，定义为： 噪声对抗估计（Noise Contrastive Estimation, NCE）：在NLP任务中一种降低计算复杂度的方法，将语言模型估计问题简化为一个二分类问题。 Introduction 无监督学习一个重要的问题就是学习有用的 representation，本文的目的就是训练一个 representation learning 函数（即编码器encod...

一般来说，神经网络处理的东西都是连续的浮点数，标准的输出也是连续型的数字。但实际问题中，我们很多时候都需要一个离散的结果，比如分类问题中我们希望输出正确的类别，“类别”是离散的，“类别的概率”才是连续的；又比如我们很多任务的评测指标实际上都是离散的，比如分类问题的正确率和F1、机器翻译中的BLEU，等等。 还是以分类问题为例，常见的评测指标是正确率，而常见的损失函数是交叉熵。交叉熵的降低与正确率的提升确实会有一定的关联，但它们不是绝对的单调相关关系。换句话说，交叉熵下降了，正确率不一定上升。显然，如果能用正确率的相反数做损失函数，那是最理想的，但正确率是不可导的（涉及到 [Math] 等操作），所以没法直接用。 这时候一般有两种解决方案；一是动用强化学习，将正确率设为奖励函数，这是“用牛刀杀...

如何计算RF 公式一：这个算法从top往下层层迭代直到追溯回input image，从而计算出RF。 [公式] 其中，RF是感受野。RF和RF有点像，N代表 neighbour，指的是第n层的 a feature在n1层的RF，记住N_RF只是一个中间变量，不要和RF混淆。 stride是步长，ksize是卷积核大小。

三维深度学习简介 多视角（multiview）：通过多视角二维图片组合为三维物体，此方法将传统CNN应用于多张二维视角的图片，特征被view pooling procedure聚合起来形成三维物体； 体素（volumetric）：通过将物体表现为空间中的体素进行类似于二维的三维卷积（例如，卷积核大小为5x5x5），是规律化的并且易于类比二维的，但同时因为多了一个维度出来，时间和空间复杂度都非常高，目前已经不是主流的方法了； 点云（point clouds）：直接将三维点云抛入网络进行训练，数据量小。主要任务有分类、分割以及大场景下语义分割； 非欧式（manifold，graph）：在流形或图的结构上进行卷积，三维点云可以表现为mesh结构，可以通过点对之间临接关系表现为图的结构。 点云的特性...

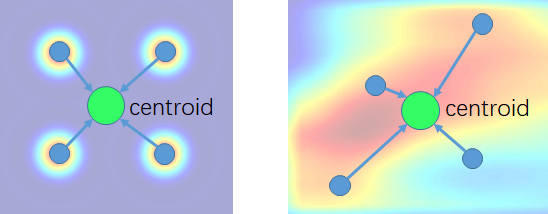
概括 这篇文章将卷积比较自然地拓展到点云的情形，思路很赞！ 文章的主要创新点：“weight function”和“density function”，并能实现translationinvariance和permutationinvariance，可以实现层级化特征提取，而且能自然推广到其deconvolution的情形实现分割，在二维CIFAR10图像分类任务中精度堪比CNN（表明能够充分近似卷积网络），达到了SOTA的性能。 缺点：每个kernel都需要由“kernel function”生成，而“kernel function”实质上是一个CNN网络，计算量比较大。 思想 察觉到：二维卷积中pixel的相对centroid位置与kernel vector的生成方式有关。 以二维卷积为例...