INCOMING TRANSMISSION

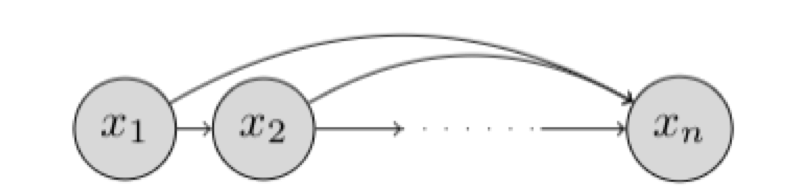
分布变换 通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量 \(Z\) 生成目标数据 \(X\) 的模型，但是实现上有所不同。更准确地讲，它们是假设了 \(Z\) 服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型 \(X=g(Z)\) ，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。 生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式 那现在假设 \(Z\) 服从标准的正态分布，那么我就可以从中采样得到若干个 \(Z_1, Z_2, \dots, Z_n\) ，然后对它做变换得到 \(\hat{X}_1 = g(Z_1),\hat{X}_2 = g(Z_2),\dots,\hat{X}_n = g(Z_n)\) ，我们怎么判断这个通过 \(g\)...

研究对象与基本设定 我们希望学习一个能够“生成数据”的概率模型。假设我们有一个数据集 \(D\) ，每个样本是 \(n\) 维二值向量： \(x \in \{0,1\}^n\) 我们的目标是用一个参数化分布 \(p_\theta(x)\) 去逼近真实数据分布 \(p_{\text{data}}(x)\) ，并最终能够： 密度估计 ：给定 \(x\) 计算 \(p_\theta(x)\) 或 \(\log p_\theta(x)\) 采样生成 ：从 \(p_\theta(x)\) 采样得到新的 \(x\) 表示：链式法则与自回归分解 链式法则分解联合分布 任意联合分布都可用概率链式法则分解为条件概率的乘积： \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, x_2, \dots, x_{i-1}) = \prod_{i=1}^{n} p(x_i \mid x_{<i})\] 其中： \(x_{<i} = [x_1, x_2, \dots, x_{i-1}]\) ，这意味着：只要我们能为每个维度 \(i\) 学好一个条件分布 \(p(x_i \mid...

the machine predicts any parts of its input for any observed part 这是LeCun在AAAI 2020上对自监督学习的定义，再结合传统的自监督学习定义，可以总结如下两点特征： 通过“半自动”过程从数据本身获取“标签”； 从“其他部分”预测部分数据。 个人理解， 其实任意挖掘对象之间联系、探索不同对象共同本质的方法，都或多或少算是自监督学习的思想 。 自监督学习与无监督学习的区别主要在于，无监督学习专注于检测特定的数据模式，如聚类、社区发现或异常检测，而自监督学习的目标是恢复（recovering），仍处于监督学习的范式中。上图展示了三者之间的区别， 自监督中的“related information” 可以来自其他模态、输入的其他部分以及输入的不同形式。 Self-Supervised...

简介 生成树（spanning tree） 在图论中，无向图 G=(V,E) 的生成树（spanning tree)是具有G的全部顶点，但边数最少的联通子图。假设G中一共有n个顶点，一颗生成树满足下列条件： （1）n个顶点； （2）n1条边； （3）n个顶点联通； （4）一个图的生成树可能有多个。最小生成树（minimum spanning tree， MST）/最小生成森林：联通加权无向图中边缘权重加和最小的生成树。给定无向图 G=(V,E) ， (u,v) 代表顶点 u 与顶点 v 的边， w(u,v) 代表此边的权重，若存在生成树T使得： [公式] 最小，则 T 为 G 的最小生成树。对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。最小生成树除了继承...

给一个无向图，判断其是否为一棵树。如果是树的话，所有的节点必须是连接的，也就是说必须是连通图，而且不能有环，所以就变成了验证是否是连通图和是否含有环。 [代码]

题目 中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。 例如， [2,3,4] 的中位数是 3 [2,3] 的中位数是 (2 + 3) / 2 = 2.5 设计一个支持以下两种操作的数据结构： void addNum(int num) 从数据流中添加一个整数到数据结构中。 double findMedian() 返回目前所有元素的中位数。 示例： addNum(1) addNum(2) findMedian() 1.5 addNum(3) findMedian() 2 题解 维护两个堆：大顶堆和小顶堆。并且需满足如下条件： 小顶堆的所有元素都大于等于大顶堆的所有元素。 大顶堆中的元素数量大于等于小顶堆中的元素数量。 大顶堆对应排序后的列表的左半部分；小顶堆对应排序...

[代码] 自己实现小顶堆 [代码] 变态的需求来了：给出N长的序列，求出BtmK小的元素，即使用大顶堆。 概括一种最简单的： 将push(e)改为push(e)、pop(e)改为pop(e)。 也就是说，在存入堆、从堆中取出的时候，都用相反数，而其他逻辑与TopK完全相同，看代码： [代码] 自己实现大顶堆 [代码]

二叉树结构 [代码] 递归 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：空间复杂度：O(h)，h为树的高度。最坏情况下需要空间O(n)，平均情况为O(logn) 递归1: 二叉树遍历最易理解和实现版本 [代码] 递归2: 通用模板 可以适应不同的题目，添加参数、增加返回条件、修改进入递归条件、自定义返回值 [代码] 迭代 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：O(h)，h为树的高度。取决于树的结构，最坏情况存储整棵树，即O(n) 迭代1: 前序遍历最常用模板（后序同样可以用） [代码] 迭代2: 前、中、后序遍历通用模板（只需一个栈的空间） [代码] 迭代3：标记法迭代（需要双倍的空间来存储访问状态） 前、中、后、层序通用模板，只需改...

背景 本文主要是《NICE: Nonlinear Independent Components Estimation》一文的介绍和实现。这篇文章也是glow这个模型的基础文章之一，可以说它就是glow的奠基石。 艰难的分布 众所周知，目前主流的生成模型包括VAE和GAN，但事实上除了这两个之外，还有基于flow的模型（flow可以直接翻译为“流”，它的概念我们后面再介绍）。事实上flow的历史和VAE、GAN它们一样悠久，但是flow却鲜为人知。在我看来，大概原因是flow找不到像GAN一样的诸如“造假者鉴别者”的直观解释吧，因为flow整体偏数学化，加上早期效果没有特别好但计算量又特别大，所以很难让人提起兴趣来。不过现在看来，OpenAI的这个好得让人惊叹的、基于flow的glow模型，估...

💡 原本随机采样的DDPM模型中，也隐含了一个确定性的采样过程DDIM，它的连续极限也是一个ODE。 细想上述过程，可以发现不管是“DDPM→DDIM”还是“SDE→ODE”，都是从随机采样模型过渡到确定性模型，而如果我们一开始的目标就是ODE，那么该过程未免显得有点“迂回”了。在本文中，笔者尝试给出ODE扩散模型的直接推导，并揭示了它与雅可比行列式、热传导方程等内容的联系。 Rectified Flow 理论推导 微分方程 像GAN这样的生成模型，它本质上是希望找到一个确定性变换，能将从简单分布（如标准正态分布）采样出来的随机变量，变换为特定数据分布的样本。flow模型也是生成模型之一，它的思路是反过来，先找到一个能将数据分布变换简单分布的可逆变换，再求解相应的逆变换来得到一个生成模型。 ...

背包问题