INCOMING TRANSMISSION

76. 最小覆盖子串 题目 给定两个字符串 s 和 t ，长度分别是 m 和 n ，返回 s 中的 最短窗口 子串 ，使得该子串包含 t 中的每一个字符（ 包括重复字符 ）。如果没有这样的子串，返回空字符串 "" 。 测试用例保证答案唯一。 示例 1： 输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 示例 2： 输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。 示例 3: 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。 提示： m == s.length n == t.length 1 <= m, n <= 10 5 s 和 t 由英文字母组成 题解 这是一个经典的 滑动窗口 (Sliding Window) 问题 我们需要维护一个动态的窗口 [left, right] ： 右移扩大 ：不断移动...

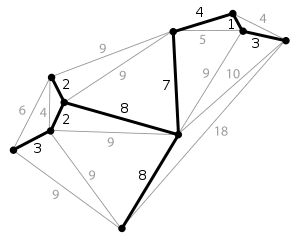
简介 生成树（spanning tree） 在图论中，无向图 G=(V,E) 的生成树（spanning tree)是具有G的全部顶点，但边数最少的联通子图。假设G中一共有n个顶点，一颗生成树满足下列条件： （1）n个顶点； （2）n1条边； （3）n个顶点联通； （4）一个图的生成树可能有多个。最小生成树（minimum spanning tree， MST）/最小生成森林：联通加权无向图中边缘权重加和最小的生成树。给定无向图 G=(V,E) ， (u,v) 代表顶点 u 与顶点 v 的边， w(u,v) 代表此边的权重，若存在生成树T使得： [公式] 最小，则 T 为 G 的最小生成树。对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。最小生成树除了继承...

给一个无向图，判断其是否为一棵树。如果是树的话，所有的节点必须是连接的，也就是说必须是连通图，而且不能有环，所以就变成了验证是否是连通图和是否含有环。 [代码]

题目 中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。 例如， [2,3,4] 的中位数是 3 [2,3] 的中位数是 (2 + 3) / 2 = 2.5 设计一个支持以下两种操作的数据结构： void addNum(int num) 从数据流中添加一个整数到数据结构中。 double findMedian() 返回目前所有元素的中位数。 示例： addNum(1) addNum(2) findMedian() 1.5 addNum(3) findMedian() 2 题解 维护两个堆：大顶堆和小顶堆。并且需满足如下条件： 小顶堆的所有元素都大于等于大顶堆的所有元素。 大顶堆中的元素数量大于等于小顶堆中的元素数量。 大顶堆对应排序后的列表的左半部分；小顶堆对应排序...

[代码] 自己实现小顶堆 [代码] 变态的需求来了：给出N长的序列，求出BtmK小的元素，即使用大顶堆。 概括一种最简单的： 将push(e)改为push(e)、pop(e)改为pop(e)。 也就是说，在存入堆、从堆中取出的时候，都用相反数，而其他逻辑与TopK完全相同，看代码： [代码] 自己实现大顶堆 [代码]

二叉树结构 [代码] 递归 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：空间复杂度：O(h)，h为树的高度。最坏情况下需要空间O(n)，平均情况为O(logn) 递归1: 二叉树遍历最易理解和实现版本 [代码] 递归2: 通用模板 可以适应不同的题目，添加参数、增加返回条件、修改进入递归条件、自定义返回值 [代码] 迭代 时间复杂度：O(n)，n为节点数，访问每个节点恰好一次。 空间复杂度：O(h)，h为树的高度。取决于树的结构，最坏情况存储整棵树，即O(n) 迭代1: 前序遍历最常用模板（后序同样可以用） [代码] 迭代2: 前、中、后序遍历通用模板（只需一个栈的空间） [代码] 迭代3：标记法迭代（需要双倍的空间来存储访问状态） 前、中、后、层序通用模板，只需改...

背包问题

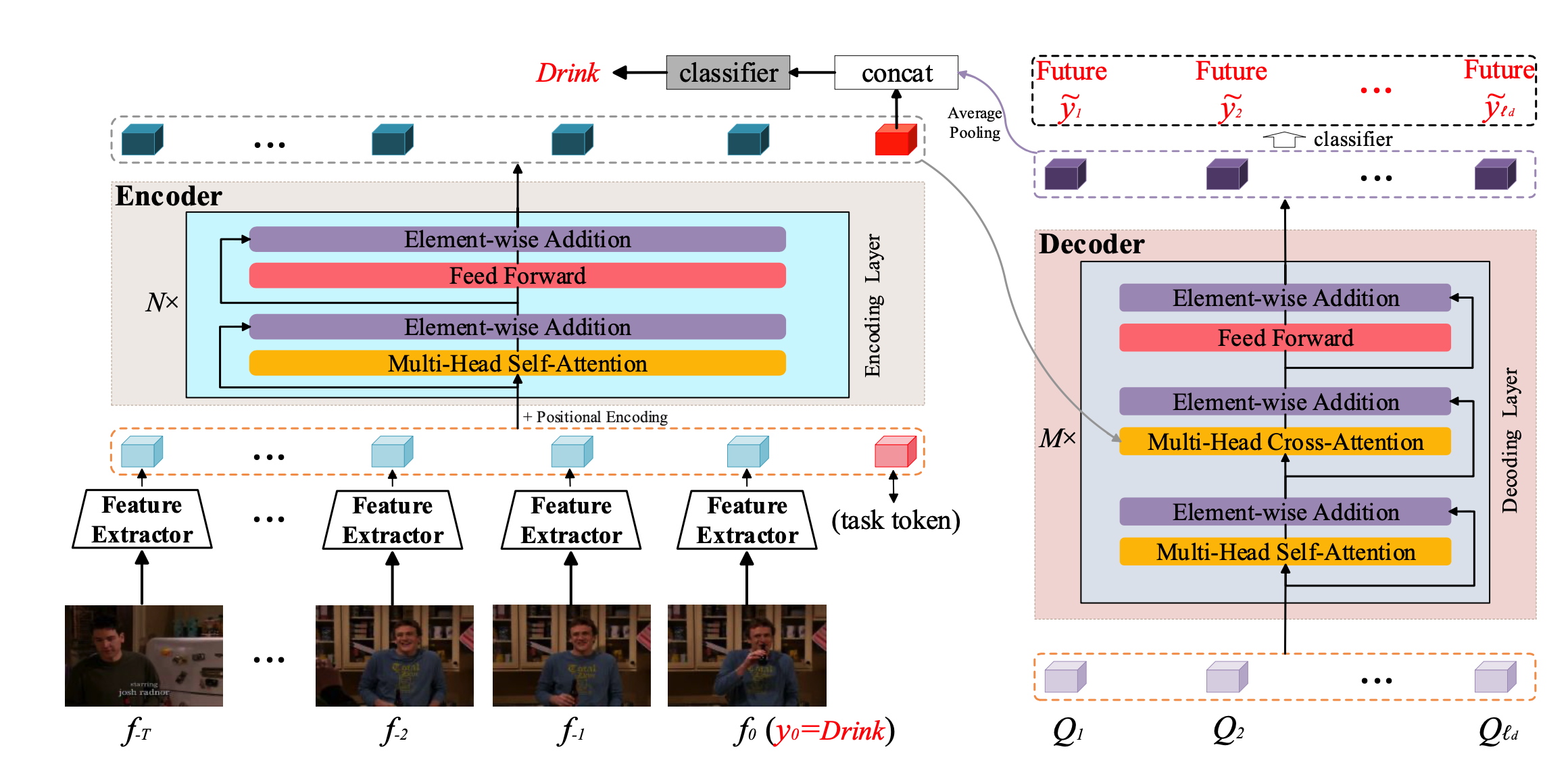
简介 之前的很多方法都是用RNN的结构去构建时序上的依赖关系，但是RNN的结构的缺点是不能并行操作，且存在梯度消失的现象。所以本文就是将之前的RNN的结构改为Transfomer的形式。延续了之前TRN的整个网络的框架，也是结合了对未来帧的预测与历史帧的表示相结合来对当前的动作进行预测。 方法 整个网络框架如上图所示， Encoder就是利用transfomer对longrange的历史和目前帧进行特征表示，其中要说明的一个点就是，这里的特征空间包含T个历史特征，当前窗口的特征以及一个task token，这个task token的作用可以从下图看出来 这幅图对比的是输入进classifier的特征与网络输入的特征的相似性，可以看出w/o task token 对应的是当前t=0时刻的特征，...

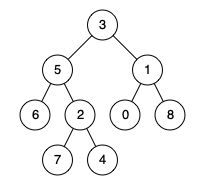
题目 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。” 示例 1： 输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出：3 解释：节点 5 和节点 1 的最近公共祖先是节点 3 。 示例 2： 输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出：5 解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。 示例 3： 输入：root...

题目 Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array. Note: The number of elements initialized in nums1 and nums2 are m and n respectively. You may assume that nums1 has enough space (size that is equal to m + n) to hold additional elements from nums2. Example: [代码] Constraints: 10^9 <= nums1[i], nums2[i] <...

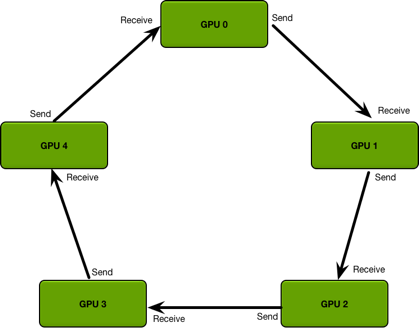
Quick Start 一个最简单的DDP Pytorch例子！ 环境准备 PyTorch(gpu)=1.5，python=3.6 推荐使用官方打好的PyTorch docker，避免乱七八糟的环境问题影响心情。 [代码] 代码 单GPU代码 [代码] 加入DDP的代码 [代码] DDP的基本原理 大白话原理 假如我们有N张显卡， 1. （缓解GIL限制）在DDP模式下，会有N个进程被启动，每个进程在一张卡上加载一个模型，这些模型的参数在数值上是相同的。 1. （RingReduce加速）在模型训练时，各个进程通过一种叫RingReduce的方法与其他进程通讯，交换各自的梯度，从而获得所有进程的梯度； 1. （实际上就是Data Parallelism）各个进程用平均后的梯度更新自己的参数，...